ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Shinde Dinesh 1, Solanki Pradip 2, Dr. Deshmukh D.S.3, Shekhawat S. P.4 P.G. Student, Department of Mechanical Engineering, SSBT’s COET, Jalgaon, Maharashtra, India1 Assistant Professor, Department of Mechanical Engineering, SSBT’s COET, Jalgaon, Maharashtra, India2 Professor, Department of Mechanical Engineering, SSBT’s COET, Jalgaon, Maharashtra, India3 Associate Professor, Department of Mechanical Engineering, SSBT’s COET, Jalgaon, Maharashtra, India4. |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper optimization technique, Simulate annealing Algorithm(SA) is studied & applied to optimize Suspension system of automobile. Suspension system is collection of springs & dampers. Selection of values of stiffness of the spring & damping values of dampers is the important task, because ride comfort of the driver is depend on this. This selection is done here with the help of SA. Programming has been developed in MATLAB 7.5, in which the steps of SA are followed to get the output as a seat acceleration, which is measure of ride, with input values of stiffness & damping constants. Principle behind optimization by SA is a naturally serial algorithm, but its behaviour can be controlled by the cooling schedule. Convergence of this method has been plotted with no. of generations
Keywords |
| Initial Temperature, job Scheduling, SA, Seat acceleration |
INTRODUCTION |
| Suspension system is main part of any automobile [1]. Optimization is a process of finding minimum or maximum of a function which is constraint or unconstraint. Number of optimization techniques are available now a day [2]. Some of the available techniques of optimization are Genetic Algorithm (GA) [3] & Simulated Annealing Algorithm (SA), etc. Simulated annealing (SA) is a random-search technique which exploits an analogy between the way in which a metal cools and freezes into a minimum energy crystalline structure (the annealing process) and the search for a minimum in a more general system; it forms the basis of an optimization technique for combinatorial and other problems[4]. Simulated annealing was developedin 1983 to deal with highly nonlinear problems. SA approaches the global maximization problem similarly to using a bouncing ball that can bounce over mountains from valley to valley. It begins at a high "temperature" which enables the ball to make very high bounces, which enables it to bounce over any mountain to access any valley, given enough bounce. It begins at a high "temperature" which enables the ball to make very high bounces, which enables it to bounce over any mountain to access any valley, given enough bounces [5]. As the temperature declines the ball cannot bounce so high, and it can also settle to become trapped in relatively small ranges of valleys. A generating distribution generates possible valleys or states to be explored. An acceptance distribution is also defined, which depends on the difference between the function value of the present generated valley to be explored and the last saved lowest valley. The acceptance distribution decides probabilistically whether to stay in a new lower valley or to bounce out of it. All the generating and acceptance distributions depend on the temperature [6]. |
II. DESIGN PARAMETERS OF SUSPENSION SYSTEM |
| Suspension system consists of group of springs, group of dampers, location of the springs & dampers. So the Design Parameters for this Suspension System are: |
| 1. Stiffness of the springs. |
| 2. Maximum deflection of the springs. . |
| 3. Location of the spring & dampers on the chassis. |
| 4. Damping value & their capacities of the Dampers. |
| 5. Deflection of Tires |
III. SCOPE FOR OPTIMUM DESIGN OF SUSPENSION SYSTEM |
| At the time of design of any automobile (i.e. car) we just think about the aerodynamic outer shape of the automobile. We did not concentrate on the suspension system. But now days a great attention is to be paid on the ride comfort of the automobile to which customer pays a lot of money. The ride comfort directly depends on the design parameters that we have seen in previous article [8]. We cannot select these design parameters randomly. There should be some relation between the values of design parameter & output ride comfort. We also have to know what will be the effect on the ride comfort on changing the design parameters. |
| So our aim is to select these Design parameters such that they will give optimum ride comfort. In this report following procedure is followed to select these design parameters for the optimum ride comfort: |
| 1. Mathematical Modeling of Automobile model is considered. |
| 2. Bounds are given to the design parameters (max & min values). |
| 3. Considering above bounds & other dimensions of the automobile a Programming is done in MATLAB 7.5 for SA. |
| 4. After running the program we can see that the ride comfort obtain is optimum for Given bounded value of design parameters. |
| 5. We check or validate the results obtain analytically. |
| 6. To select optimum ride comfort we can change the values of design parameters in the MATLAB program. So we will get directly the values of design variable which will give Optimum ride comfort. |
IV. MATHEMATICAL MODELING |
| The following is a description of the model used by A.E. Baumal et al. [2]. Same model is considered here also for analysis. Fig.4.illustrates the road vehicle suspension system considered for optimal design. The system 5 degrees of freedom are represented by the independent generalized co-ordinates: |
| q = [q1,q2,q3,q4,q5,qA,qB] |
| Which are measured from the static equilibrium position. A mathematical description of the model is expressed by the equations of motion: |
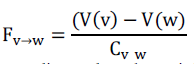 |
| This equation is same as vibration equation for multi degree of freedom system. Analysis of the suspension generally implies solving equation (1) for the time response of the system. |
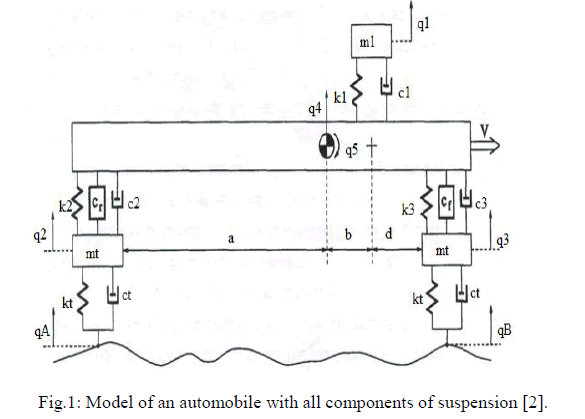 |
| There are three characteristics commonly used to assess the performance of vehicle suspension systems: |
| 1. Ride comfort, which improves as the magnitude of the seat acceleration is reduced. |
| 2. Road-holding ability or safety, which is acceptable for restricted or low tire-road contact forces and is quantified by tire deflection (e.g. the rear tire deflection q3 - qA). |
| 3. The suspension working space, which must be restricted (e.g. the rear wheel-chassis space) Ride comfort is chosen to be the most important characteristic so it is expressed in an Objective Function. Seat acceleration is the measure of ride comfort: |
| An upper bound is placed on seat comfort, considering 10 m/s2 as a maximum value of it, so that seat acceleration would be less than 10.3 m/s2 |
| Following are some constraints that are placed on the system so that it’s movement will be restricted, so that the tire deflections and relative spaces between bodies are restricted by, |
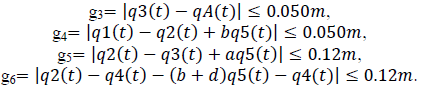 |
V. RESULTS |
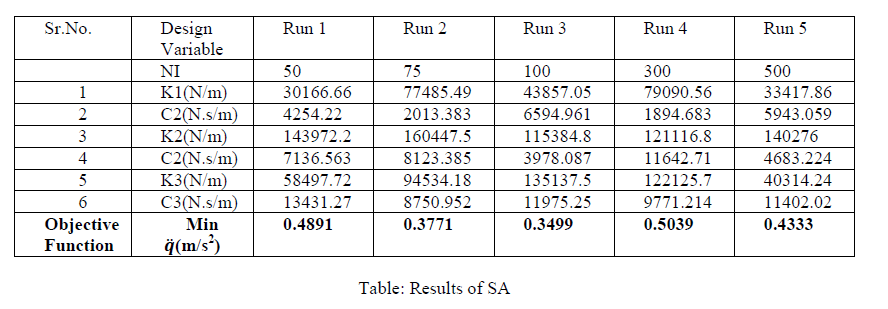
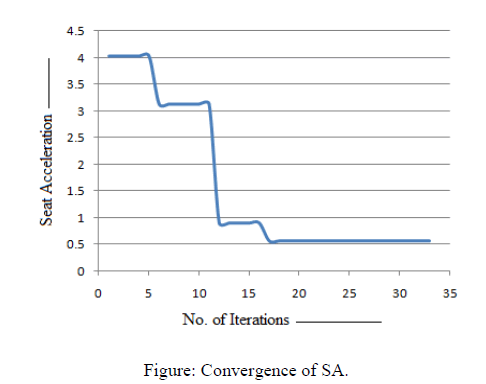
| Programming has been done in MATLAB 7.5 system for SA in which steps of flowchart are followed [10]. In above program number of iteration is taken as 1000. This number of iteration can be varied for different Run. We can take thousand of value for NI. |
 |
 |
VI. CONCLUSION |
| After studying Simulated Annealing Algorithm and applying it to suspension system of automobile by developing program in MATLAB, we come to following conclusions: |
| 1. We get minimum seat acceleration in Run 3. |
| 2. Convergence of SA is smoother with lower steps. Therefore in SA objective function value does not go to wrong direction in intermediate steps of answer |
| 3. We can use this MATLAB program to apply it on any automobile suspension system. |
| 4. We can change the values of stiffness of springs & dampers in the program to get optimum desired ride comfort or seat acceleration. If we want to manufacture springs of certain stiffness for the suspension system, before manufacturing it we can add their values in the program to check that our desired ride comfort will achieved or not. If we are not satisfied with the ride comfort obtain, we don’t go to manufacture it, rather the values of stiffness are varied to get optimum ride comfort. |
ACKNOWLEDGEMENT |
| Authors are acknowledged to Head of Mechanical Engg. Department of SSBT’s COET, Jalgaon for allowing him to use MATLAB system in CAD /CAM lab. |
References |
|