Automatic Classification of ECG Signals
with Features Extracted Using Wavelet
Transform and Support Vector Machines

Sambhu D.; Umesh A. C.

Automatic Classification of ECG Signals with Features Extracted Using Wavelet Transform and Support Vector Machines

Sambhu D.¹, Umesh A. C.²

M.Tech Student, Department of ECE, Rajiv Gandhi Institute of Technology, Kottayam, India¹
Asst. Prof, Department of ECE, Rajiv Gandhi Institute of Technology, Kottayam, India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Electrocardiogram (ECG) is one of the most widely used techniques for diagnosing cardio vascular diseases. Automatic beat segmentation and classification of ECG signal is paramount since scrutinizing each and every beat is a tedious job for even the most experienced cardiologist. In this paper, we have accurately classified and differentiated Normal and abnormal heartbeats such as left bundle branch block (LBBB), right bundle branch block (RBBB), atrial premature contractions (APC) and premature ventricular contractions (PVC), atrial premature beat (APB), Paced beats and Fusion beats with adequate levels of accuracy. At first the multi resolution analysis of ecg signal is done to denoised and extract 25 features. The mother wavelet used for decomposition was db4. The classification is implemented by using OAO (One Against One) SVM (Support Vector Machine). 7 SVM’s were trained and final grouping is done by maximum voting. ECG signals are obtained from the open source MIT-BIH cardiac arrythmia database. Experiments reveal that the overall classification accuracy is well above 97 % for all the classes.

Keywords

ECG, Arrythmia classification, discrete wavelet transform, support vector machines.

INTRODUCTION

The automatic classification of ECG signal has gained so much importance over the few decades. Apart from saving the lives of thousands, it helps cardiologist make decisions about cardiac arrythmias more accurately and easily. The ECG is a biometric signal, which records the heart’s electrical activity versus time; therefore it is an important diagnostic tool for assessing heart function [1]. An experienced cardiologist can diagnose various heart diseases by looking at the ECG waveforms printout. However, the use of computerized analysis of easily obtainable ECG waveforms can considerably reduce the doctor’s workload. This paper is aimed at developing a system that classifies the ECG signals automatically into various classes of abnormalities so that it would be easier for a doctor to verify later. A typical normal ECG signal is shown in Fig. 1. It comprises of a P wave, a QRS complex followed by a T wave. In automatic ECG classification system, it is essential to classify the ECG beat accurately.

Over the past few years, many researchers developed and utilized different techniques and algorithms to classify ECG beats, For example neural networks[2],[3], k nearest neighbour[4],[5], and support vector machines(SVM)[6],[7] which recently became a popular classification method.

In this paper, seven arrythmia conditions are investigated using DWT and SVM. They are, normal (N), paced beats (P), right bundle branch block (R), left bundle branch block (L), atria premature beat (A), fusion of paced and normal beats (F), premature ventricular contraction, premature atrial contraction. The ECG signal is first decomposed into four levels using daubechies wavelet. The multi resolution analysis (MRA) of ECG beat is done upto 4 levels. Wavelet decomposition helps in the removal of noise and base line wander. The feature vector is also formed using the coefficients obtained from WT decomposition. The seven different ECG heartbeat were taken from the MIT/BIH database[8]. This rest of the paper is organized as follows. Section 2 presents ECG signal preprocessing and feature extraction including a brief description of the DWT. Section 3 introduces SVM classification methodology for ECG signals. In Section 4 we present our experimental methodology, and Section 5 depicts results and discussion.

ECG DATA, PRE PROCESSING AND FEATURE EXTRACTION

A. MIT/BIH Database

The MIT-BIH Arrhythmia Database[8] contains 48 half-hour records obtained from 25 male and 22 female subjects studied by the BIH Arrhythmia Laboratory. The recordings were digitized at 360 samples per second per channel with 11-bit resolution over a 10 mV range. Two or more cardiologists independently annotated each record; disagreements were resolved to obtain the computer-readable reference annotations for each beat (approximately 110,000 annotations in all) included with the database.

B. DWT

Discrete wavelet transform is particularly useful for the analysis of transients, aperiodic and other non-stationary signal features. Hence it is very much useful in the processing of ECG signals[9]. The DWT employs a dyadic grid (integer power of two scaling in a and b) and orthonormal wavelet basis function as shown in (1).

where the integers m and n control the wavelet dilation and translation respectively. The dyadic grid wavelet can be written by substituting a0 = 2 and b0 = 1, as in (2)

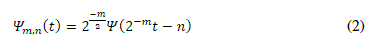Now the discrete wavelet transform (DWT) can be written as in (3)

where T_mn is known as the wavelet (or detail) coefficient at scale and location indices (m, n). The selection of the wavelet and number of decomposition levels are crucial for the analysis of ECG signals [10]. The Daubechies wavelet is conceptually more complex but, it picks up detail that is missed by the Haar wavelet algorithm [11]. Even if a signal is not well represented by one member of the db family, it may still be efficiently represented by another. Selecting a wavelet function which closely matches the signal to be processed is of utmost importance in wavelet applications[12]. Daubechies wavelet family are similar in shape to QRS complex and their energy spectrum are concentrated around low frequencies.

C. Baseline Removal and Denoising

Baseline wander has frequency contents that is between 0.15Hz and 0.3Hz. Decomposing the signal using WT into signals approximation, which are high scale low frequency components, and signals detail, which are low scale high frequency components, helps to identify wanted and unwanted components such as noise[12]. Once done, it was observed that the baseline drift is most serious at scale 8 and it was later removed.

D. Feature Extraction

A large number of possibilities have been proposed about which features to use to describe the ECG. Apart from the RR interval, which is used in most studies, almost every single published paper proposes a new set of features to be used, or a new combination of the existing ones[13],[14].

Finding the right feature combinations is, indeed, a hard task. However, if all features found in the literature were introduced, the number will be indeed too large and it would result in heavy computational cost[15]. So we selected those features that are relevant for a particular type of disease. Those features are identified from literature and are mixed to form a single feature vector that included the following types of features.

? Temporal features, which already proved in different studies to be the most relevant. This category includes heart rate and interval features.

? Morphological features, gives the characteristic morphology details that include coefficients from wavelet decomposition, their maxima minima etc.

? Statistical features completes the feature set, includes mean, variance, and other statistical moments.

The algorithms described in [10],[16],[17] are applied to find the temporal features such as ST Interval, RR Interval, Heart Rate, TT Interval, PR Interval, QT Interval, PP Interval. The statistical features includes the mean, variance, skewness, kurtosis, sum, root mean square, mean absolute deviation of the wavelet coefficients. In order to find the morphological features, the ECG signal is decomposed to level 4 using daubechies as the mother wavelet, then the maximum and minimum values of Detail coefficient and Approximation coefficients along with peak values of P, QRS and T peaks are used[18].

All these features are concatenated into a single feature vector. 25 Features are extracted for each single beat and the dimensionality of the feature vector was 52. Thus the original beat which was originally a vector of dimensionality 301 is compressed into just 52 samples. This is given as the input to the SVM classifier.

SVM CLASSIFIER

The support vector machine (SVM)[19],[20] is a training algorithm for learning classification and regression rules from data. SVMs were first suggested by Vapnik in 1995. The geometrical interpretation of support vector classification (SVC) is that the algorithm searches for the optimal separating surface. This is equivalent to maximizing the distance, normal to the hyperplane, between the convex hulls of the two classes; this distance is called the margin as depicted in Fig. 2. The Lagrangian for this problem is given in Equation (4).

where are the Lagrange multipliers, one for each data point. The solution to this quadratic programming problem is given by maximising L. The Lagrange multipliers are non-zero when , vectors for which this is the case are called support vectors since they lie closest to the separating hyperplane[19].

The SVM can be used to learn non-linear decision functions by first mapping the data to some higher dimensional feature space and constructing a separating hyperplane in this space. Denoting the mapping to feature space by (5).

The kernel function, K ( x, z )=Φ ( x )^T Φ( z ) allows us to construct an optimal separating hyperplane in the space H . For implementation in MATLAB, a package called LIBSVM was used[21].

EXPERIMENTAL METHODOLOGY

In the experimental setup as shown in Fig. 4, the ECG signal from the database are first filtered with the scales obtained from the Wavelet decomposition. Preprocessed and segmented beats serves as input to further processing. These beats are labelled and the labels are stored in a separate annotation files (*.atr). These labels are extracted from the label file and is used for generating the label file. The segmented ECG beat along with its label is used to the train the SVM. Initially the fiducuial points are detected after wavelet decomposition. These are the temporal features

Then the detail and approximation coefficients are used to find the morphological features. Finally the statistical features are found using the built in statistical toolbox of Matlab. Thus all the algorithms are implemented in Matlab 2009 running in a Pentium dual core processor with 3GB RAM. SVM implementation is done with LIBSVM software package that supports binary class only. Multiclass SVM can be obtained by using the One Against One (OAO) approach[22]. linear kernel is used in all SVM’s.

The outputs are combined using Maximum voting technique. If we give the same beat to all the SVM models, the one model that is originally intended to that particular class will produce a ‘1’ while all others generate ‘0’ output. Thus we can recognize that particular class which generates a ‘1’ as the class into which the test beat falls. TABLE I shows the names of the records used for training and testing of the classifier

RESULTS AND DISCUSSION

A. Results

The obtained results and confusion matrices are given below in TABLE II. It was seen that some models gave reduced accuracy. This is because as the number of classes increases the classification accuracy reduces. All the SVM models did not gave exactly the same performance.

In TABLE II, the accuracy obtained for each class is given. The thick green lines separate confusion matrices of various classes. Since individual SVM’s are binary classifiers, each confusion matrix has two rows and columns. The principal diagonal elements represents those ECG beats correctly classified and the off diagonal elements of the matrix indicates the incorrect classification. From this we calculate performance parameters such as sensitivity, selectivity, accuracy and the values so obtained are given in the last row of TABLE II. The training and testing datasets for each class is prepared by mixing same class beats from various ECG records and is labelled as positive examples. The negative examples are formed by mixing equal number of beats from rest of the all classes. The sum of all the elements of a confusion matrix gives the number of test samples in the dataset. The performance parameters are calculated from the confusion matrix as follows. Sensitivity is defined as in (6), is a measure of the capacity of test the positive samples.

Specificity is defined as (7), is a measure of capacity of test the negative samples.

Accuracy is defined as (8).

CONCLUSION

Some models gave high amount of accuracy while others gave less accuracy. The reason is that all the features does not work equally good for all the classes. Some features that works well for some type of classes will affect like noise for some other classes. The solution for this is implementing feature selection algorithm[24]. The performance of the wavelet based feature extraction was a suitable one. The combination of the temporal, statistical and wavelet features was an effective method in the classification of cardiac abnormalities. The advantage of the SVM classifier using the given feature vector is its ease of implementation and simplicity. The result of the implementation is compared with other algorithms is given in TABLE III. The algorithm has to be modified to process real time data coming from an ECG machine. In future we will try to develop this project in a fully open platform. We can improve the accuracy by including more features. This will result in prolonged training and testing. Including more features has advantages of improved accuracy since the chances of finding an optimal subset of relevant features is always more. But the problem is the intense computation that might be carried out to do the classification. This again can be tackled by using various dimensionality reduction techniques such as LDA, PCA[25].

Tables at a glance


Table 1	Table 2	Table 3

Figures at a glance


Figure 1	Figure 3	Figure 4

References

John R Hampton, The ECG Made Easy, 6th ed. Churchill, Livingstone.

G. Herrero, A. Gotchev, I. Christov and K. Egiazarian, “Heartbeat classification using independent component analysis and matching pursuits,” IEEE International Conference Acoustic. Speech and Signal Processing, 2005.

R. Ghongade and A. Ghatol, “An Effective Feature Set for ECG Pattern classification,” Lecture Notes in Computer Science, Vol.4901, pp.25-32, 2007.

I. Christov, I. Jekova, and G. Bortolan,“Premature ventricular contraction classification by the Kth nearest-neighbours rule,” Institute of Physics Publishing, Physiological Measurement, Vol.26, pp.123-130, 2005.

I. Christov, G. Herrero, V. Krasteva, I. Jekova, A. Gotchev and K. Egiazarian,“Comparative study of morphological and time-frequency ECG descriptors for heartbeat classification,” Medical Engineering & Physics, 2006.

K.-T. Chou and S.-N. Yu,“Categorizing Heartbeats by Independent Component Analysis and Support VectorMachines, ”Eighth International Conference on Intelligent Systems Design and Applications, isda, Vol.1, pp.599-602, 2008.

E. Zellmer, F. Shang and H. Zhang,“Highly Accurate ECG Beat Classification Based on Continuous Wavelet Transformation and Multiple Support Vector Machine Classifiers,”BMEI’, pp.1-5, 2009.

MIT-BIH arrhythmia database, http://www.physionet.org/physiobank/ database/mitdb/

Paul S Addison; Topical Review on ‘Wavelet transforms and the ECG: A review’, Institute Of Physics Publishing, Published 8 August 200

S. Z.Mahmoodabadi, A. Ahmadian, M. D. Abolhasani1, ‘ECG Feature Extraction Using Daubechies Wavelets’, Proceedings of the fifth IASTED International Conference on Visualizing, Imaging and Image Processing, September 2005.

B. Priyadarshini, R.K.Ranjan, Rajeev Arya, ‘Determining ECG characteristics using wavelet transforms’, International Journal of Engineering Research & Technology (IJERT), Vol. 1 Issue 6, August – 2012

C. Saritha, V. Sukanya, Y. Narasimha Murthy, ‘ECG Signal Analysis Using Wavelet Transforms’, Journal of physics, February 2008

Chua Kuang Chua, Vinod Chandran, Rajendra U Acharya, and Lim Choo Min, “Cardiac Health Diagnosis Using Higher Order Spectra and Support Vector Machine,” Open Medical Informatics Journal, Vol. 3, p-1, 2009.

De Lannoy, G. ; Francois, D. ; Delbeke, J ; Verleysen, M.: “Feature Relevance Assessment in Automatic Inter-Patient Heart Beat Classification,” International Joint Conference on Biomedical Engineering Systems and Technologies, 2010.

Tanis Mar ,Sebastian Zaunseder, Juan Pablo Martinez, Mariano Llamedo and Rudiger Poll, ‘Optimization of ECG Classification by Means of Feature Selection’, IEEE Transactions On Biomedical Engineering, Vol. 58, No. 8, August 2011

P. Sasikala, R.S.D. Wahidabanu ‘Robust R Peak and QRS detection in Electrocardiogram using Wavelet Transform’, (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 1, No.6, December 2010

C. Saritha, V. Sukanya, Y. Narasimha Murthy, ‘ECG Signal Analysis Using Wavelet Transforms’, Journal of physics, February 2008

Can Ye, Miguel Tavares Coimbra and B.V.K. Vijaya Kumar, “Arrhythmia Detection and Classification using Morphological and Dynamic Features of ECG Signals,” 32nd Annual International Conference Of The IEEE EMBS

C.J.C. Burges. A tutorial on support vector machines for pattern recognition. Mining and Knowledge Discovery, 2(2):1-47, 1998

http://research.microsoft.com/pubs/67119/svmtutorial.pdf

http://www.csie.ntu.edu.tw/~cjlin/libsvm/

J. Milgram, M. Cheriet, R.Sabourin, “One Against One or “One Against All”: Which One is Better for Handwriting Recognition with SVMs?”

Narendra Kohli, Nishchal K. Verma, and Abhishek Roy, “SVM based Methods for Arrhythmia Classification in ECG,” Int’l Conf. on Computer & Communication Technology, 2010

P. Pudil, J. Novovicova, and J. Kittler, “Floating search methods in feature selection,” Pattern Recognit. Lett., vol. 15, no. 11, pp. 1119–1125, 1994.

Zhang, H., & Zhang, L. Q., “ECG analysis based on PCA and Support vector Machines,” Neural Networks and Brain, 2005