1Department of Statistics, Faculty of Mathematical sciences, University of Tabriz, Iran
2Department of Statistics, Universit Paris-Dauphine, 75775 Paris Cedex 16, France
Received: 01/09/2015 Accepted: 30/11/2015 Published: 15/12/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In order to generate discrete distributions based on continuous distributions, various techniques have been implemented and their parameters estimate and characteristics have also been discussed through classical methods. But a few number of essays have dealt with such distribution through Bayesian estimate parameters, mainly due to their complexity and increasing number of parameters. This paper dealt with Bayesian estimate discrete Burr distribution with two parameters. In order to simulate the results, Monte-Carlo and Metropolis-Hastings algorithms were used.
Discrete Burr distribution, Random variable, Bayesian estimate, Numerical methods
Discrete distributions are very important in modeling the real life plan. Many essays have been published on the study and applications of discrete distributions. Using these techniques, one can transform the continuous distributions into the discrete ones. Katz [1], Roknabadi, et al. [2], Krishna and Pundir [3] have introduced di erent methods for generating discrete families of distributions. The discrete Burr distribution with two parameters is one of them. If the parameters of this distribution are constant, then to estimate them, Maximum Likelihood and Moment Methods [4] are used, but supposing that the variables were random, then the Bayesian method should be used. In fact, one cannot be sure that the parameters of a distribution are constant values to specify them to prior distribution parameters and calculate their Bayesian estimate. In case they are not calculable through the usual methods of Bayesian estimator, the approximate methods such as numerical integration, Monte-Carlo and Laplace's approximation methods [5] will be used. This paper has used these methods to estimate the Bayesian discrete Burr distribution parameters. A lifetime random variable X follows the Burr-XII, or simple Burr, Br (α,β )1 if its probability density function is as follows:
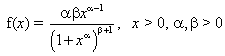
In this case, for each x > 0, the survival function is
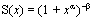
The risk rate is
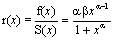
The second risk rate is
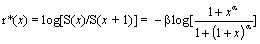
The r's moment is
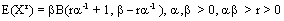
which 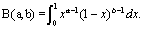
In special case, if α =1, Pareto distribution Par(β)2 with its reliability characteristics will be obtained. If times are grouped into unit intervals, the discrete observed variable dX = [X], the largest integer less than or equal to X, will have the probability function as follows:
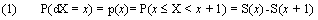
which x = 0, 1,2,…..
Krishna and Pundir [1] applied this method to study the discrete Burr and Pareto distributions. Using the equation (1), the probability mass function of discrete Burr distribution DBD (α,θ)3 can be dened as follows:
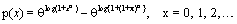
It is important to note that S(x) for Br (α, β) and DBD(α,θ) is equal at the correct points of x. Bayesian estimate of parameters in the case n sample will be calculated in next section.
If X1,…, Xn has discrete Burr distribution with α and θ parameters, then
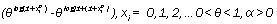
To calculate Bayesian estimators, three following cases should be considered:
Suppose that θ has beta distribution with a and 1 parameters, so the previous density of θ is:
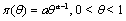 (3)
(3)
Then
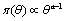 (4)
(4)
And
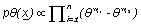 (5)
(5)
Which 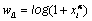 and
and 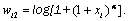
Using (4) and (5), posterior density function of θ is obtained as follows:
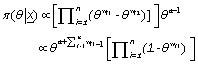 (6)
(6)
Which 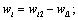 so
so
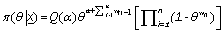 (7)
(7)
Now, the marginal distribution of X1,…, Xn is obtained by integrating (6) over θ :
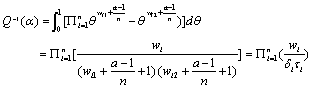
Which 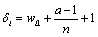 and
and 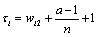 ; then
; then
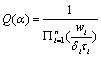 (8)
(8)
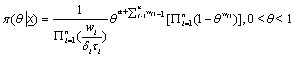 (9)
(9)
Supposing a squared-error loss function and known prior, the Bayesian estimate θ parameter will be as follows:
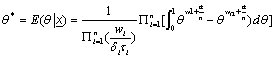 (10)
(10)
Which
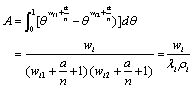
Which 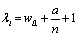 and
and 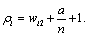
By putting A in (10) the following will be obtained:
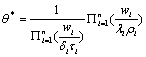 (11)
(11)
So the Bayesian estimator θ parameter in this case is 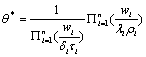
In this case α is assumed to have unknown prior distribution (ie, there is no prior knowledge about the distribution of α ), thus, the prior density of α can be written as follow:
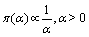 (12)
(12)
And
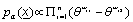 (13)
(13)
which 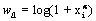 and
and 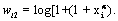
using (12) and (13) we get:
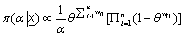 (14)
(14)
Thus,
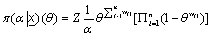 (15)
(15)
Which 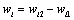
Z(θ ) is calculated as follows:
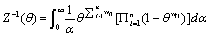
Since the posterior density obtained in (15) doesn't belong to the known distributions, therefore, the numerical methods will be used through R software. Let's assume X1,…, X25 is a random sample of discrete Burr distribution and θ = 0.1, 0.2, 0.3, using Metropolis-Hastings algorithm [6] a proper normal distribution will be considered as, q presupposition for parameter α, and applying the aforementioned algorithm through R software, a Markov chain of 10,000 posterior distribution members will be generated. If the loss function is squared error, the mean of this Markov chain, is the Bayesian estimate of the parameters, and if the loss function is the absolute error, then, the median of this Markov chain is the Bayesian estimate of the parame-ters. The results of these simulations are shown in the Tables 1 and 2 respectively.
In this case suppose that α has unknown prior, and θ has Beta distribution as in the first case, both α and θ are independent. α and θ joint prior density will be as follow:
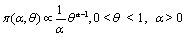
on the other hand, we know that:
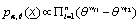 (18)
(18)
Which 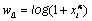 and
and 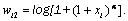
using (17) and (18) we have:
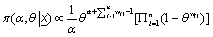 (19)
(19)
Then
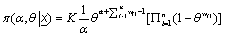 (20)
(20)
where K is a constant value, it will be calculated as follows:
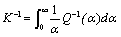 (21)
(21)
which 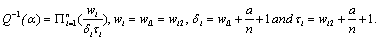
where
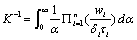 (22)
(22)
Considering the posterior density obtained in (20) does not belong to known distributions, therefore, the numerical methods will be used through R software. Let's assume X1,…, X25 is a random sample of discrete Burr distribution and a = 3, using Metropolis- Hastings algorithm [2], the proper uniform and normal distributions will be considered as q presupposition for θ and α parameters respectively, and applying the aforementioned algorithm through R software, a Markov chain of 10,000 posterior distribution members will be generated. If the loss function is squared error, the mean of this Markov chain is the Bayesian estimate of the parameters, and if the loss function is the absolute error, then, the median of this Markov chain is the Bayesian estimate of the parameters. The results of these simulations are shown in the Tables 3 and 4 respectively.
This study dealt with the Bayesian analysis of discrete Burr distribution parameters with two parameters in three n case, and using the proper prior distributions for the parameters, the Metropolis-Hastings method for numerical parameters
1Continuous Burr distribution with parameters α and β
2Continuous Pareto distribution with parameter β
3Discrete Burr distribution with parameters α and θ