ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Nauman Mohammed1, Islam Nazrul2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Structures in high seismic risk areas may be susceptible to severe damage in a major earthquake. For the variety of structures and possible deficiencies that arise, several retrofitting techniques can be considered. Bracing system is one of the retrofitting techniques and it provides an excellent approach for strengthening and stiffening existing building for lateral forces. Also, another potential advantage of this system is the comparatively small increase in mass associated with the retrofitting scheme since this is a great problem for several retrofitting techniques. Our ability to build seismically safe structures with adequate seismic resistance has increased significantly in the past few decades. Many reinforced concrete frame structures built in seismically active areas are expected to perform inadequately in a seismic event. Braced frames are known to be efficient structural systems for buildings under high lateral loads such as seismic or wind loadings. The fact that the lateral resistance of frame can be significantly improved by the addition of a bracing system has led to the idea of retrofitting seismically inadequate reinforced concrete frames with steel bracing system. Steel bracing systems have both practical and economical advantages. The potential advantage of bracing system is the comparatively small increase in mass associated with the retrofitting scheme since this is a great problem for several retrofitting techniques. The application of steel bracings is faster to execute. The steel bracings are usually installed between existing vertical members. Furthermore, if it is used in the structure, the minimum disruption of the building is obtained.
Keywords |
| Retrofitting, Reinforced Cement Concrete, Bracing, Lateral Loads |
INTRODUCTION |
| During earthquake motions, deformations take place across the elements of the load-bearing system as a result of the response of buildings to the ground motion. As a consequence of these deformations, internal forces develop across the elements of the load-bearing system and displacement behaviour appears across the building. The resultant displacement demand varies depending on the stiffness and mass of the building. In general, buildings with higher stiffness and lower mass have smaller horizontal displacements demands. On the contrary, displacement demands are to increase. On the other hand, each building has a specific displacement capacity. In other words, the amount of horizontal displacement that a building can afford without collapsing is limited. The purpose of strengthening methods is to ensure that the displacement demand of a building is to be kept below its displacement capacity. This can mainly be achieved by reducing expected displacement demand of the structure during the strong motion or improving the displacement capacity of the structure. |
RELATED WORK |
| Badoux and Jirsa investigated numerically the behaviour of RC frames retrofitted with external bracing. Researchers stated that the lateral resistance of the existing frame structures is inadequate for two reasons. First, the perimeter frames, which feature weak short columns, are likely to fail in an undesirable mode. Secondly, code provisions may have been upgraded several times since construction, so that current seismic design loads are more than the original values. |
| Youssef, Ghaffarzadeh and Nehdi also investigated the use of internal steel bracing for seismic performance of reinforced concrete frames. In their study, the use of concentric internal steel bracing for new construction was investigated experimentally. Ghobarah and Abou Elfath have investigated analytically the seismic performance of a low-rise non-ductile reinforced concrete building rehabilitated using eccentric steel bracing. |
OBJECTIVE OF THIS PAPER |
| The objective of this paper is to evaluate the response of braced and unbraced structure subjected to seismic loads and to identify the suitable bracing system for resisting the seismic load efficiently. |
MODELLING & ANALYSIS OF BUILDING |
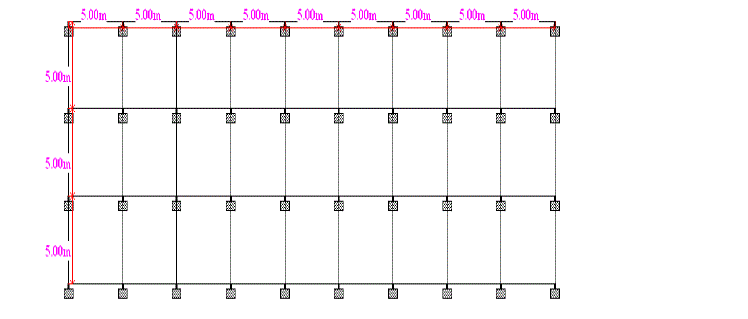
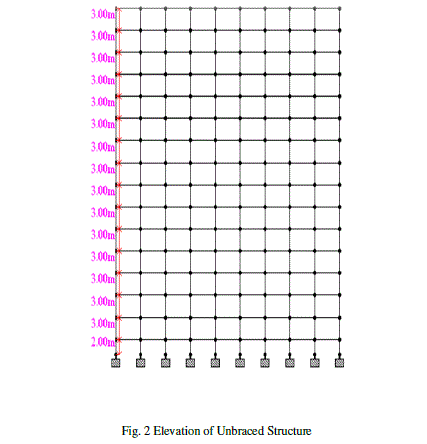
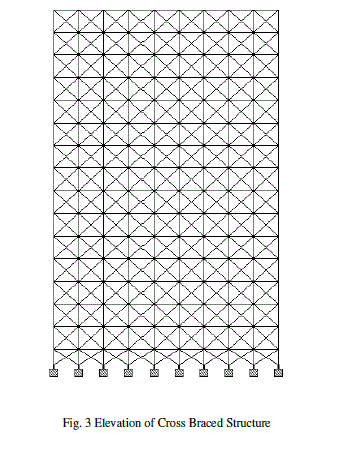
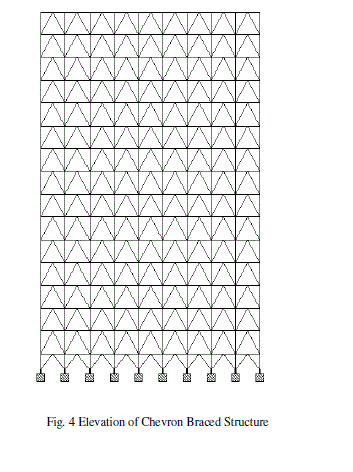
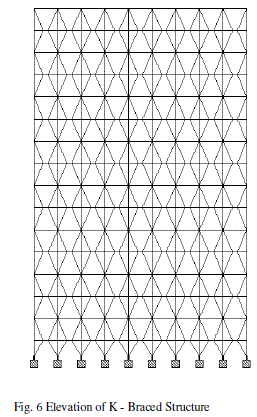
| The analysis of G+14 floors is carried out using STAAD V8i software for special moment resisting frame situated in zone 4.The RCC G+14 structure is analysed without bracings and with different types of bracings system. Bending moments, shear forces, storey shears, story drifts and axial forces is compared for all type of structural systems i.e. braced and unbraced structural system. |
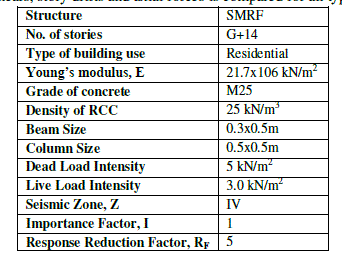 |
| TABLE 1.MODELING DATA FOR BUILDING |
 |
 |
 |
 |
 |
 |
RESULTS |
 |
 |
 |
 |
 |
 |
 |
DISCUSSION ON RESULTS |
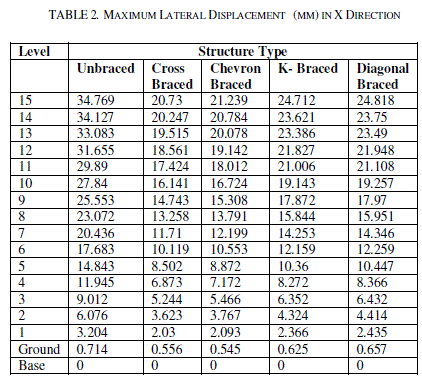
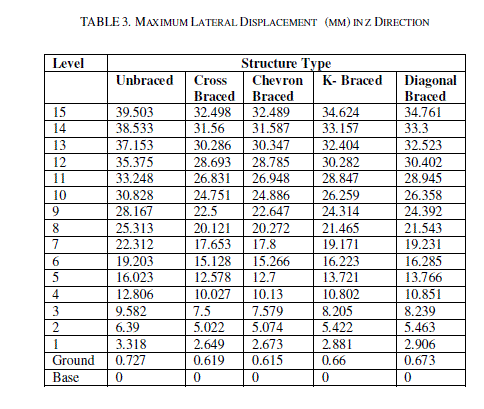
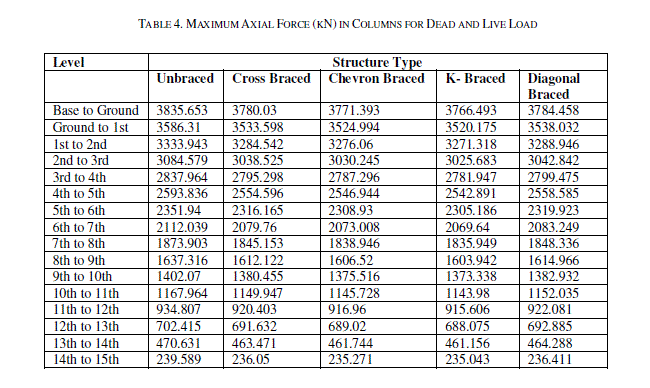
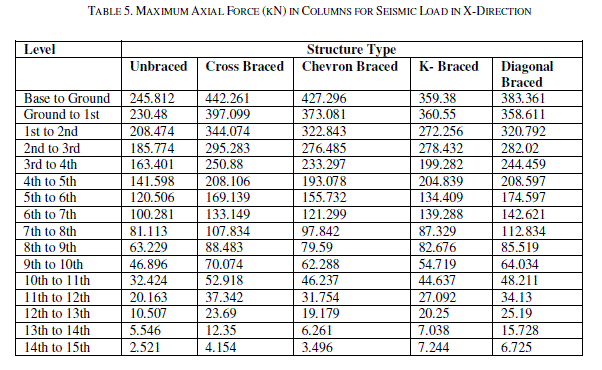
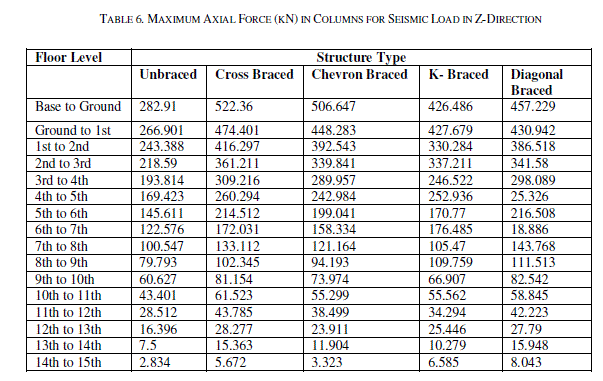
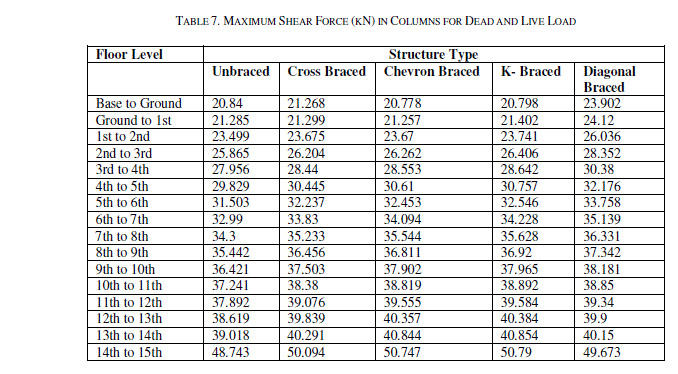
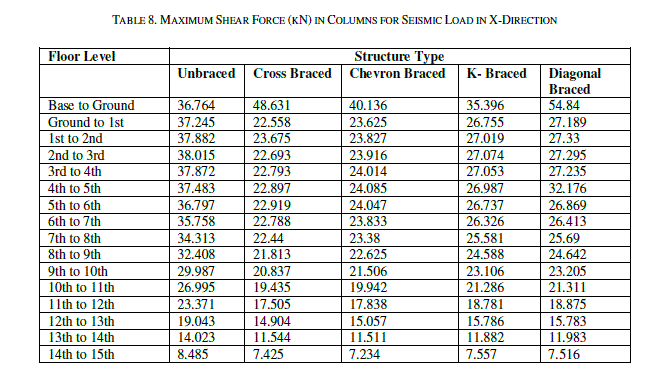
| Table 2 & Table 3 show the maximum lateral displacement for seismic load in X & Z direction respectively at different storey levels. The lateral displacements of the structure for various bracings system are compared. The maximum lateral displacement at terrace level in X direction is 34.769mm, 20.73mm, 21.239mm, 24.712mm and 24.818mm for unbraced, cross braced, chevron braced, K-braced & diagonal braced structural systems. Whereas the lateral displacement at the same storey level in Z direction for the above said structural systems are 39.503mm, 32.498mm, 32.489mm, 34.624mm & 34.761 mm respectively. It is noted that the lateral displacement is drastically reduced after the application of bracings system. Maximum reduction in the lateral displacement is observed after the application of cross bracings. Table 4, Table 5 & Table 6 show the maximum axial force in columns for dead & live load, seismic load in Xdirection and seismic load in Z direction respectively. The axial forces of the structure for various types of bracings systems are compared. For dead & live load case, it is observed that the axial force in the structure has been reduced after the application of the bracing system but the axial force values in the columns for the seismic loads are increased. The axial force for seismic load in X direction for unbraced structure at the base level is 245.812 kN which has been increased considerably to 442.261 kN, 427.296 kN, 359.38 kN and 383.361 kN for cross braced, chevron braced, Kbraced & diagonal braced structure respectively. The maximum increment in axial force is observed in cross braced structure. Table 7, Table 8 & Table 9 show the shear forces at different stories for all the structural systems i.e. unbraced, cross braced, chevron braced, K-braced & diagonal braced structural systems for dead & live load, seismic load in X direction and seismic load in Z direction respectively. It can be seen that the shear force for column for dead & live load for unbraced and different types of braced structural systems is almost the same, but there is a considerable change in the shear forces for seismic load in both the directions for unbraced and different types of braced structural systems. It is observed that maximum shear force for the unbraced structure for seismic load at base level in X direction is 36.764 kN and it has been increased to 48.631 kN, 40.136 kN, 35.396 kN and 54.84 kN for cross braced, chevron braced, K-braced & diagonal braced structure respectively. It has been reduced to 8.485 kN for unbraced and 7.425 kN, 7.234 kN, 7.557 kN and 7.516 kN cross braced, chevron braced, K-braced & diagonal braced structure respectively at terrace level. Table 10, Table 11 & Table 12 show the maximum values of bending moments at different stories for all the structural systems i.e. unbraced, cross braced, chevron braced, K-braced & diagonal braced structural systems for dead & live load, seismic load in X and Z direction respectively. It can be seen that the bending moments for columns for dead & live load for unbraced and different types of bracing system is almost the same. It can be seen that the maximum bending moments for unbraced, cross braced, chevron braced, K-braced, and diagonal braced structure at base level is 63.126 kN-m, 68.364 kN-m, 59.3 kN-m, 60.304 kN-m and 79.711 kN-m respectively. It has been reduced to 16.694 kN-m, 14.334 kN-m, 14.058 kN-m, 14.684 kN-m and 14.628 kN-m for unbraced, cross braced, chevron braced, Kbraced, and diagonal braced structure at terrace level respectively. |
CONCLUSION |
| After the analysis of the structure with different types of structural systems, it has been concluded that the displacement of the structure decreases after the application of bracing system. The maximum reduction in the lateral displacement occurs after the application of cross bracing system. Bracing system reduces bending moments and shear forces in the columns. The lateral load is transferred to the foundation through axial action. The performance of cross bracing system is better than the other specified bracing systems. Steel bracings can be used to retrofit the existing structure. Total weight of the existing structure will not change significantly after the application of the bracings. |
References |
|