ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
H. R. Ghate1, Atish S. Sontakke2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A Bianchi type-IX cosmological model has been investigated in the presence of perfect fluid with disordered radiation in Barbers (Gen. Relat. Gravit.14, 117, 1982) second self-creation theory of gravitation. The field equations have been solved by applying special law of variation for generalized Hubble’s parameter given by Bermann (NuovoCimento 74, 182, 1983). Some physical properties of the models are also discussed.
Keywords |
| Self-Creation Cosmology, Radiating Model, Bianchi type-IX |
INTRODUCTION |
| Einstein’s theory of general relativity (Einstein 1916) is a very successful gravitational theory in describing the gravitational phenomena which also served as a basis for the models of the universe. Einstein pointed out that general relativity does not account satisfactorily for inertial properties of matter i.e. Mach’s principle is not substantiated by general relativity. There have been several attempts to generalize the general theory of gravitation by incorporating Mach’s principle and other desired features which were lacking in the original theory. Barber [1] has proposed two self-creation theories of gravitation by modifying Brans-Dicke theory and general relativity. Brans [2] has pointed out that Barber’s first theory is in agreement with experiment but is actually inconsistent in general as it violates equivalence principle. However second theory is a modification of general relativity to a variable G-theory and predicts local effects that are within the observational limits. In this theory, the scalar field does not gravitate directly but simply divides the matter tensor, acting as a reciprocal gravitational constant. Here the scalar field couples to the trace of the energy momentum tensor. |
| Pimentel [3] and Soleng [4] have discussed FRW models by using a power law relation between the expansion factor of the universe and the scalar field. Singh [5], Reddy [6] and Reddy et al. [7] have studied Bianchi type space-times solutions in Barber’s second theory of gravitation while Reddy and Venkateswarlu [8] presented Bianchi type-VI0 cosmological model in Barber’s second self-creation theory of gravitation. Shanthi and Rao [9] studied Bianchi type II and III space-times in this theory, both in vacuum as well as in presence of stiff fluid. Ram and Singh [10] have discussed the spatially homogeneous and isotropic Robertson-Walker and Bianchi type-II models of the universe in Barber’s self-creation theory in presence of perfect fluid by using gamma law equation of state. Pradhan and Pandey [11], Pradhan and Vishwakarma [12], Panigrahi and Sahu [13], Venkateshwarlu and Kumar [14], Singh and Kumar [15], Venkateswarluet al. [16], Reddy and Naidu [17] and Katoreet al. [18] are some of the authors who have studied various aspects of cosmological models in Barber’s second self-creation theory. Katoreet al. [19] have studied accelerating and decelerating hypersurface-homogeneous cosmological models in Barbers’s second self-creation theory. Recently, Mahanta [20] have studied dark energy (DE) models with variable EoS parameter in self-creation theory of gravitation. |
| Bianchi type-IX cosmological models are very popular for relativistic studies. These models are also used to examine the role of certain anisotropic sources during the formation of large scale structures as we seen the universe today. Chakraborty [21], Raj Bali and Dave [22], Raj Bali and Yadav [23] have studied Bianchi type-IX string as well as viscous fluid models in general relativity. Pradhan [24] have studied some homogeneous Bianchi type-IX viscous fluid cosmological models with varying ïÃÂÃÅ . Tyagiet al. [25] have obtained Bianchi type-IX string cosmological models for perfect fluid distribution in general relativity. Ghate and Sontakke [26-27] have studied Bianchi type-IX cosmological models in different context. |
| In this paper, Bianchi type-IX cosmological model has been investigated in the presence of perfect fluid with disordered radiation. The solution to the Einstein field equations are obtained using the condition that expansion scalar is proportional to the shear scalar given by Berman. The physical and geometrical properties of model are also discussed. |
II. METRIC AND FIELD EQUATIION |
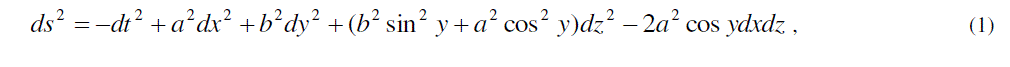 |
| which represents disordered radiation of matter distribution. The field equations (2) and (3), for the metric (1) with the help of equations (4)-(6) in Barber’s second self-creation theory can be explicitly written as |
 |
 |
| whereoverdot (Ãâ¹Ãâ¢) denotes partial differentiation with respect to t. |
III. SOLUTIONS OF THE FIELD EQUATIONS |
| Equations (9)-(12) are four highly non-linear equations in six unknowns a, b,& p,and T . We can introduce more conditions either by an assumption corresponding to some physical situation or an arbitrary mathematical supposition, however these procedures have some drawbacks. Physical situation may lead to differential equations which will be difficult to integrate and mathematical supposition may lead to a non-physical situation. Two additional conditions relating these unknowns are required to obtain explicit solutions of the systems. |
| (i) Firstly, we assume that the expansion in the model is proportional to the shear . This condition leads to |
| wherem is proportionality constant. |
| The motive behind assuming condition is explained with reference to Thorne [28], the observations of the velocity redshift relation for extragalactic sources suggest that Hubble expansion of the universe is isotropic today within ïÃâû 30 percent (Kantowski and Sachs [29]; Kristian and Sachs [30]). To put more precisely, red-shift studies place the limit |
 |
| (ii) Secondly, the law of variation of Hubble’s parameter yields a constant value of deceleration parameter. Such type of relations have already been considered by Berman [32] for solving FRW models. We consider the constant deceleration parameter model defined by |
 |
 |
IV. PHYSICAL PROPERTIES OF THE MODEL |
| The model (20) represents Bianchi type-IX disordered radiating cosmological model which is physically significant for the study of early stages of evolution of the universe. |
 |
V. RESULTS AND DISCUSSION |
 |
VI. CONCLUSION |
| In this paper, we have investigated radiating Bianchi type-IX cosmological model in Barbers second self-creation theory of gravitation using the law of variation for the Hubbles parameter which yields a constant value of decelerating parameter stated by Berman. At initial epoch the model starts evolving with zero volume and expands for large time |
 |
| anisotropic and represents the early stages of the universe which matches the results of recent experiments which shows that there is certain amount of anisotropy in the universe. Hence the anisotropic models are important. It is well known that the scalar fields have considerable effects on cosmological scale. The radiating model obtained here, will help to study early era in self-creation cosmology. Also, this study of cosmological models and understanding our universe through these models has astrophysical importance and relevance. |
References |
|