Blurred Image Recognition by Legendre
Moment Invariants

S.Rajeswari

Blurred Image Recognition by Legendre Moment Invariants

S.Rajeswari
Assistant Professor, Department of ECE, BIST, Bharath University, Chennai, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Processing blurred images is a key problem in many image applications. Existing methods to obtain blur invariants which are invariant with respect to centrally symmetric blur are based on geometric moments or complex moments. In this paper, we propose a new method to construct a set of blur invariants using the orthogonal Legendre moments. Some important properties of Legendre moments for the blurred image are presented and proved. The performance of the proposed descriptors is evaluated with various point-spread functions and different image noises. The comparison of the present approach with previous methods in terms of pattern recognition accuracy is also provided. Theexperimental results show that the proposed descriptors are more robust to noise and have better discriminative power than the methods based on geometric or complex moments.

INTRODUCTION

An image may be defined as two dimensional function f(x, y), x and y are spatial coordinates. Digital image processing refers to processing of digital images using digital computers and the digital are represents by picture elements or pixels. Computing the average intensity of an image would not considered an image processing operation. They are three types of processes

1. Low level processes

2. High level processes

3. Mid-level processes

In the low level process , input and output are represented by images, the mid-level process are characterized by the factor , input are images and the output are attributes extracted from images , and the high level is represented by image analysis. Image in the form of slide, photograph is first digitized and stored as a matrix of binary digits in computer memory. The digitized images are processed and or displayed on a high resolution monitor. For display , image is stored in rapid accessThe widely accepted standard linear model describes the imaging process by a convolution of an unknown original image f(x,y) with a space invariant point spread function (PSF) h(x,y)which refreshes the monitor at 30 frames/s for continuous display.

One of the frequent tasks in image processing is the recognition of an image

( or , more frequently, of an object on the image) against images stored in a database. Whereas the images in the database are supposed to be ideal, the acquired image represents the scene mostly in an unsatisfactory manner. Because real imaging systems as well as imaging conditions are imperfect, an observer image represents only a degraded version of the original scene. Blur is introduced into the captured image during the imaging process by such factors as diffraction, lens aberration, wrong focusing, and atmospheric turbulence.

Image processing is a very active area that has impacts in many domains from remote sensing, robotics, traffic surveillance, to medicine. Image recognition methods are mainly applicable in automatic target recognition and tracking, character recognition, 3-D scene analysis and reconstruction.

The image is captured through the camera , if that image is in unsatisfactory manner means that image represents the blurred image. The images are affected because of the following factors,

they are,

1. Wrong focusing

2. Atmospheric turbulence

3. Lens aberration

4. Out of focus

Some kind of noises ( e.g Gaussian noise, Salt & pepper noise, additive noise with different standard deviations).

g(x,y) = (f * h) (x,y)

where,

g(x,y) represents the observed image

h(x,y) describes the imaging system it is supposed to be unknown

IMAGEPROCESSING TOOLBOX

MATLAB is a high performance language for technical computing. It integrates computation, visualization, and programming in an easy to use environment where problems and solutions are expressed in familiar mathematical notation. The name MATLAB stands for Matrix Laboratory. MATLAB was originally written to provide easy access to matrix software developed. The toolbox supports a wide range of image processing operations, including Spatial image transformation, Morphological operations, Transforms, Image analysis and enhancement, image restore, Deblurring

LITERATURE REVIEW

EXISTING SYSTEM

Since the recent advances in electrical devices enable widespread uses of mobile cameras, degradation of the image caused by camera motion has been considered a key issue. However, most conventional research has not been able to guarantee satisfactory quality of the resultant image because of the ill-posed characteristic of the image restoration model. In classical image deblurring approaches, a point spreadfunction (PSF) is assumed to be known. Based on the known PSF, image deconvolution has been applied to restore images. In real applications, however, the PSF is scarcely known. Therefore, the PSF is estimated in the space domain or frequency domain.

The difficulties of PSF estimation and image deconvolution give rise to recent research efforts. These efforts attempt to solve the deblurring problem with additional conditions. The characteristics of multi-exposed images have been exploited to obtain an image adopting the advantages of each of the images. Otherwise, the PSF is estimated from a shorttime exposed image, and deconvolution is applied based on the estimated PSF. Even though recent techniques produce satisfactory results, the computational complexities of these methods can be a problem when implemented into real applications. Also, since a short-time exposed image tends to have a low signal-to-noise ratio (SNR), the information from this image is not always reliable.

In this letter, we propose a novel image deblurring algorithm using multiple blurred images to reconstruct an original scene. The mutually different pieces of information from the multiple blurred images of a scene are merged in the frequency domain by using the projection onto convex sets (POCS). When mergingthe information, the concept of the fuzzy convex set is exploited to express the reliability of each spectrum component. Since only reliable frequency component is extracted from each blurred image, the resultant image contains the maximum possible information of the scene. Thus, image blur is efficientlyreduced.

The difficulty of image deblurring comes from the fact that the original image spectrum is damaged by the blur. Therefore, a recovery of the distorted image spectrum by using all available information is a major challenge of image deblurring. In classical image deblurring approaches using single blurred image, the PSF is assumed to be known or is estimated. However, a priori information is not always available, and an estimation error of the PSF can produce severe deblurring artifacts. Therefore, in this letter, we focus on the case where differently blurred multiple images on the same scene are available. Also, since image registration is not a concern in this work, we assume that each blurred image is aligned, so that there is no grid mismatch among the blurred images .Based on this assumption, we merge the multiple blurred images to reconstruct the deblurred image.

PROPOSED SYSTEM

We propose a new method to derive a set of blur invariants based on orthogonal Legendre moments (for a recent survey on moments. The organization of this paper is as follows: in Legendre moment blur invariant, we review the theory of blur invariants of geometric moments and the definition of Legendre moments. In Section Blur invariants of Legendre moments, we establish a relationship between the Legendre moments of the blurred image and those of the original image and the PSF. Based on this relationship, a set of blur invariants using Legendre moments is provided. The experimental results for evaluating the performance of the proposed descriptors are given,. Finally, some concluding remarks are provided.

MAIN SYSTEM

The main purpose of the system is to recognize the uncleared version of the images. The following diagram shows the reorganizationsystem. It has the following process,

a) Read the blurred image from the workspace

b) Obtain the point spread function of the image

c) Moment invariant method

d) Blur invariants

e) Deblurring

Finally we can recognize the blurred image using the Legendre’s moment invariant method and reconstructed the original image by using the same method. These functions are performed by using the MATLAB software. The image data bases are already stored in the MATLAB workspace; compare the blurred image with the prestored databases in the workspaces. After comparing applying the moment’s invariants method for recognition. Comparison is performed in the whole images that mean it will compare the nearest pixel values by using the orthogonal moment invariants.

BLURRED IMAGE

Blurred image is the uncleared version of the original image, that is original image is corrupted by some noises, these kinds of noises are affect the original version of the scene. Image is captured through the real sensing system but all the real sensing systems are not imperfect their affect the original version.

These are affected because of the following factors,

Wrong focusing

Lens abbreation

Out of focus

Some kind of noises.

The following diagram shows the blurred image,

MOMENT INVARIANTS

An important class of geometric invariants is based on the image moments. By definition, the central moments are invariant to image shift. For discrete image f (n), the (p, q)’th central moment is given by

where (n1 , n2 ) is the centroid of the image. For the regular moments, (n1 , n2 ) = (0, 0).Normalized central moments, given by

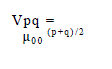are invariant to shift and scaling.

The first moment invariants that were used for visual pattern recognition were proposed by Hu (1961), who introduced seven moment invariants to rotation of 2-D objects consisting of second and third order moments. The four simplest of these invariants are given below:

By substituting μ pq in (.2) with normalized central moments ν pq , invariants to similarity transformation, i.e., shift, rotation, and scaling, are obtained.

There are various applications and improvements of these invariants (Flusser 2006).The moment invariants have been applied for instance to character and object recognition (Belkasim et al. 1991) and image registration (Goshtasby 1985). Hupkens & de Clippeleir (1995) proposed normalization of the moment invariants for contrast invariance. Wong et al. (1995) presented a method of generating moment invariants of up to the fifth order. Wallin & Kiibler (1995) introduced a method for the generation of complete sets of rotation invariants using Zernike moments. Abu-Mostafa & Psaltis (1984) proposed the use of complex moments for rotation invariance. Complex moments are given by

where i denotes the imaginary unit.

Flusser (2000) suggested forming the rotation invariants as follows: let n ≥ 1 and ki , pi , and qi be non-negative integers so that Σi=1 ki (pi − qi ) = 0. Then the rotation n invariants are obtained by

i=1

Flusser (2000) also introduced a method of forming a basis for the invariants, which is the smallest set of the invariants by which all others can be expressed .Reiss (1991) and Suk & Flusser (1993) introduced independently moment invariants to affine transformation of images. Later Suk & Flusser (2004) proposed a graph based method of generating invariants systematically. Yang & Cohen (1999) proposed affine invariants based on cross-weighted moments. This approach results in more robust invariants than those based on regular moments, at the expense of computational cost.

IMAGE BLUR AND DEBLURRING

Blur is generated to images by the non-ideal image capturing process. The effect of blurring is the same as lowpass filtering the image. Typical causes of blurring are motion between the camera and the scene during exposure, and an out of focus optical system. In addition to the blur, the captured image always contains some amount of noise. The noise results from various factors such as non-ideal sensors and quantization of the digital images. The blur invariants discussed later in this thesis are based on the assumption that the blur obeys a certain model.

OUT OF FOCUS BLUR

Appears in the image if the lens system of the camera is not focused for the correct distance to the scene. Because the aperture of the lens is circular, the blurred image of a point source is a small disk. In general, the extent of the blur depends on the focal length, the aperture size, and the distance between the camera and the object, and it is not constant in the whole image. When the scene is relatively planar and orthogonal to the camera, the out of focus blur can be estimated by a uniform and circular PSF,which is spatially invariant according to (2), and is given in the continuous form by

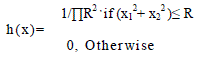where R is the radius of the blur (Lagendijk & Biemond 2005). Figure illustrates a discrete out of focus blur PSF h(n) corresponding to R = 3. Figure illustrates the corresponding magnitude response |H(u)| in the Fourier domain, again with an oscillating shape, and lowpass behavior. This time zero-pattern is circular. Figure illustrates an image which is out of focus blurred using the PSF in Figure.

ATMOSPHERIC TURBELENCE BLUR

It is encountered for example in remote sensing. The PSF of the blur depends on various factors, such as the air temperature and the wind speed, but for relatively long exposure time, it can be estimated using a Gaussian distribution, given by h(x) = C exp ( - x₁ ²+ x₂ ²/ 2σG ²)

where variance σG determines the severity of the blur, and constant C is chosen so that the sum of the coefficients is equal to one (Lagendijk & Biemond 2005). Figure llustrates a discrete atmospheric turbulence blur PSF h(n) corresponding to σG = 9/4 and Figure shows the corresponding magnitude response |H(u)|. In the continuous case, the magnitude response would be a pure 2-D Gaussian, but in the discrete case, it contains some oscillation due to the finite support of the PSF. Figure illustrates an image which is Gaussian blurred using the PSF in Figure . Figure shows an arbitrary blur PSF, the magnitude response being shown in Figure. The corresponding blurred image is illustrated in Figure . The existing blur invariant image features are based on the assumption that the PSF of the blur is spatially invariant and centrally symmetric with respect to the origin . These conditions are met by the above mentioned forms of motion, out of focus, and atmospheric turbulence blur PSFs.

CONCLUSION

Image restoration, or deblurring, is concerned with the reconstruction of the original uncorrupted image from the blurred and noisy image by an inverse operation. The operation is different to artificial image sharpening. For spatially invariant blurring, the deblurring is done by deconvolution. There are many problems in deblurring including the estimation of the PSF of the blur and the difficulties of deconvolution.


Figure 3.2	Figure 3.3	Figure 4

References

J. Liu and T. X. Zhang, “Recognition of the blurred image by complex moment invariants,” Pattern Recognit. Lett., vol. 26, no. 8, pp.1128–1138, 2005.
A. Stern, I. Kruchakov, E. Yoavi, and S. Kopeika, “Recognition of motion-blurred images by use of the method of moments,” Appl. Opt., vol.41, no. 11, pp. 2164–2172, 2002.
J. Flusser and B. Zitova, “Combined invariants to linear filtering and rotation,” Int. J. Pattern Recognit. Artif. Intell., vol. 13, no. 8, pp.1123–1136, 1999.
J. Lu and Y. Yoshida, “Blurred image recognition based on phase invariants,” IEICE Trans. Fundam. Electron. Comm. Comput. Sci., vol.E82A, pp. 1450–1455, 1999.
J. Flusser , T. Suk, and S. Saic, “Recognition of blurred images by the method of moments”, IEEE Trans. Image Process., vol, no. 3, pp.533-538, Mar.1996
X. H. Wang and R. C. Zhao, “Pattern recognition by combined invariants,”Chin. J. Electron., vol. 10, no. 4, pp. 480–483, 2001.He is with the Department of Computer Science and Engineering, Southeast University, China. His recent.