Boundary Extraction Using Poincare Map
Method

Ruchita V. Indulkar; Sanjay D. Jondhale

Boundary Extraction Using Poincare Map Method

Ruchita V. Indulkar, Sanjay D. Jondhale

ME Computer, Department of Computer Engineering,SVIT, Chincholi, Nashik, Maharastra,India.
Associate Professor, Department of Computer Engineering, SVIT, Chincholi, Nashik, Maharastra,India.

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Now a day’s active contours or snakes are used in many image processing applications, especially for locating the object boundaries and edge detection. But the problems of these models are initialization and poor convergence to deep concavities of the boundary and particularly equilibrium issues in the vector field. In the proposed method first the ISAF field is generated which is composed of swirling and attracting component (DETF & DEPF respectively). Then with the help of dynamical system limits cycles are set / located by Newton- Raphson algorithm in the Poincare section. And integral equations are used to connect these boundaries.

Keywords

Image segmentation, Poincare map method, Newton-Raphson algorithm, dynamical system.

INTRODUCTION

Segmentation is a necessity of today’s world, especially in the field of Machine Vision, Medical imaging, object detection, Face detection or recognition, IRIS etc. Segmentation is defined as dividing an image into multiple segments (set of pixels) and is typically used to locate objects and boundaries in images. It is a process of assigning a label to every pixel in an image such that pixels with same labels share certain characteristics. In the area of segmentation active contour models, snakes are widely used. But there are some difficulties with these active contours like –

1. Their evolution direction must be predefined

2. They may evolve slowly or may even converge wrongly as the initial contour are far away from the boundary or may have been crossed the desired boundary.

3. They cannot progress into deep concavities of the boundaries as they stick to local minima of the energy function.

There were also another types of methods evolved as a solution for the above difficulties they were as –

i. Region based method

ii. Pulling the active contour to the expected boundary by external or internal force field.

The above two methods were able to move the active contour across the local minima but there were some unpreventable conflict components which stopped the active contour to locate exact boundaries.

Thus, the proposed system is different as compared to other traditional contour methods. The system will first generate the ISAF field for a given image. The ISAF field is composed of the two components

Swirling and attracting components also known as the diffused ETF (DETF) and diffused edge perpendicular flow (DEPF) near the image boundary. Then treating these swirling components as limit cycle in a dynamical system will correspond to the desired objects.

A periodic orbit which initial conditions within a section of space, which leaves that section afterwards and observe the point at which the orbit first returns to the section and then creates a map to send the first point to the second. Hence name Poincare map. Then the Poincare section is generated for the ISAF field. And the Newton- Raphson method is used to locate the limits on to the boundary and then lastly these boundaries are linked by integral equation.

Section II describes the previous work on the several ACMs (Active Contour Methods) and discusses some weaknesses of the existing methods. Sections III describe the proposed system in detail that includes generation of ISAF field and how to achieve boundary extraction and object segmentation in dynamical system and highlights the algorithms. Section IV which describes the input in terms of dataset to the proposed method followed by the expected result in Section V. Section VI concludes and gives the future scope of the system.

LITERATURE SURVEY

Active contours are used in many image processing applications, especially for locating the object boundaries and edge detection and image segmentation. Thus, may image segmentation algorithms have been developed as: Clustering methods, Compression-based methods, Histogram-based methods, Edge detection methods, Region growing methods, Partial differential equation-based method like:

a. Parametric methods

b. Level set methods

The author Kass et al proposed a method that moved the explicit parametric curves to extract objects in images. They defined active contours as energy-minimizing splines directed by external forces that pull the curves toward features such as lines and edges. They also define an internal energy term which is used to impose smoothness on the moving curve. Because of the way the contours move while the energy is minimized they call them snakes. Pros: These typical ACM or Snakes has some internal drawbacks, such as it is unable to handle topological changes and its dependency of parameterization and is also possess inability to detect concave objects and its sensitive to initialization.

The authors Xu and prince proposed a new model for traditional contours called as gradient vector flow (GVF). The GVF calculates the diffusion of gradient vectors of an edge map (gray scale or binary) and also provides with flexible initialization of contour and improved convergence to boundary concavities and has a larger capture range. Pros: Though thee model have good flexibility to initialization and can converge to boundary concavities the difficulty with this model is that it forces the snake into long and thin boundary indentions. So the same authors again proposed a new model which work similar to the GVF but can deal with the long and thin boundary indentations known as generalized gradient vector flow (GGVF).

The authors Bing li and Scott T. Acton in year 2007 presented vector field convolution (VFC) to address the disadvantages of the GVF, GGVF and traditional snakes such as high computational cost, noise and parameter sensitivity etc. by calculating the external force and this force is calculated by convolving vector field with edge map from the image.

Pros: one disadvantages of VFC may be that the weak edges may get drown beneath the strong edges.

Researches Muriel Gastaud and Michel BarlaudFellow, proposed a variational approach based on an active contour technique including a shape prior defined as a functional of the distance between the active contour and a contour of reference. The contour of reference may be defined by an operator for interactive image segmentation, or it can be deduced from a previous segmentation in video segmentation and tracking. They avoided the parametric transformation constraint by allowing a free form deformation between the contour of reference and the active contour.

Osher and Sethian presented PSC schemes, for moving surfaces under their curvature. The algorithms were dependent on numerically solving Hamilton-Jacobi equations with viscous terms, using approximation techniques from hyperbolic conservation laws.

Authors Caselles, Kimmel and Sapiro presented a framework, in which they denoted that boundary detection can be considered equivalent to finding a curve of minimum length and this has given a new approach to detect boundary via ACM that are based on the local minima distance calculation. Then considering this contour as zero level-set of a 3D function they reduced a geodesic curve computation.

All the above models have the difficulties of initialization and poor convergence to deep concavities of the boundary and equilibrium issues in the vector field which stops the contour

IMPLEMENTATION DETAIL

The objective of the proposed system is:

1. Object segmentation using Poincare map method in a define vector field in dynamical systems.

2. Generating the ISFA filed for the image which contains two swirling and attracting components for an image.

3. Set the initial sates on the basin of attraction (the limit cycles) and calculate the convergence of the states with the limit cycles of an image and simultaneously also calculate the orbits.

4. The objects’ boundaries are linked by integral equations with the corresponding converged states and periods.

In the proposed system object segmentation is achieved by the Poincare map method within the dynamical systems. Thus, this is achieved by the following modules:

A. ISAF Field.

B. In the Framework of Dynamical Systems.

C. Poincare Map and Newton-Raphson algorithm.

D. Multiple objects Segmentation.

A. ISAF Field

In this, an ISAF (interpolated swirling and attracting flow) field for an image is generated. It is composed of two components, diffused ETF i.e. DETF: swirling component and diffused edge perpendicular flow i.e. DEPF: attracting component. DETF is a swirl around the object’s boundary and is nonzero in the homogenous regions. When a DEPF is generated and if there is an eddy present near the object boundary any particle away from the image map will move to the boundary along the streamlines (direction of flow). DEPF acts as the attracting component. In ISAF field generated for an image will produce a periodical streamline along the boundary and the vector field components are directed to the boundary and move along these boundary in rounded fashion.

B. In the framework of dynamical system

After generating the ISAF field for the given image where its eddies or swirl correspond to the object’s boundaries. This state the limit cycles in the dynamical systems, where dynamical system is defined as array of Ordinary DE (ordinary differential equations). The eddies here can be considered as limit cycles of a vector field that belong to dynamical system.

These limit cycles are located, including their periods and candidate points on the limit cycles.

C. Poincare Map and Newton-Raphson algorithm

Poincare (definition): it is the intersection of periodic orbit in the state space of continuous dynamical system with a certain lower dimensional subspace called as Poincare section. This Poincare section is used to set the limit cycles for which the Poincare section lies. The Poincare section is described as follows:

The Newton-Raphson method is used for zero computation of periods in Poincare section. As poor the value of period is, newton-raphson sequence causes positive Poincare on χ 0 far away from χ 0 even if it is on the limit cycle.

D. Multiple Object Segmentation

In this phase after the ISAF field has been generated for an image N distinct initial states randomly in image domain can be placed which corresponds to the number of objects in an image. Then, these N states will move within the flow field and finally will move to the object’ boundaries. In this for each initial states Poincare section are defined and with the help of newton-raphson algorithm the fixed point for corresponding Poincare map is calculated (i.e. determines the N converged states on the boundaries) as well as simultaneously calculate the periods implicitly. The representation for the object’s boundaries with N converged states is:

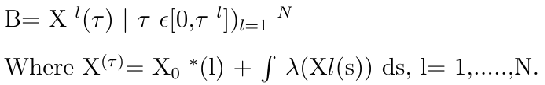Here B denotes the object boundaries with N converged states, X (τ) denotes the periods for l=1….N and N are the number of initial states on the boundary.

ALGORITHMS

1. ISAF Field generation:

This calculates the gradient & gradient magnitude for an observed image.

a) Input the value of sigma and maxedges.

b) Calculate the edge map

f=grad (Sigma (x, y)*I(x, y))

c) Calculate the value of g.

g[i]=Math.exp(-(fx[i]*fx[i]+ y[i]*fy[i])/(k*k))

d) Calculate the value of h = 1 - g

e ) Calculate the gradient magnitude terms u(x, y),v(x, y))

du /dt = g(|grad f|) Δ(u) - h(|grad f|)*(u - fx)

dv /dt = g(|grad f|) Δ(v) - h(|grad f|)*(v - fy)

f) Repeat the step 3 to 5 until maxegdes.

2. Within the framework of Dynamical systems:

a) Define the input frequency.

b) Set the initial time and final time.

c) Set the initial state of X0.

d) tspan = [t0, tfinal ]

//contains other specific points of integration.

e) Generate [t, x] by creating an Ordinary Differential Equation solver.

f) Plot the results.

3. Poincare section:

a) Initialize all the parameter for beginning of steady state.

b) Calculate the length of t and store it.

c) Calculate the Poincare section for each pixel(x,y) as

Poincare_x= [x (round (m*per), res: m, 1]

Poincare_y= [x (round (m*per), res: m, 2]

d) Plot the Poincare section functions.

DATASET

Any image can be applied as an input to the system. It can be any coloured or Gray-scaled image for which the gradient is calculated.

RESULTS

The proposed system can be applied to any image such as medical image, real image that is coloured or binary edged and also having deep concavities. In this, we will first place the initial states randomly in the image domain then by using the newton-raphson algorithm we will converge to the converged states on the boundaries as well as we will find the length of the objects known to be periods for converged states and finally, object boundaries will be represented by the integral equations. As compared to the previous contour methods, this method can locate exact boundary as well as can achieve multiple segmentation when applied to any image and will prove better than the traditional contour methods as the proposed method is capable of locating not only close but exact boundary in an image domain.

CONCLUSIONAND FUTURE WORK

With the help of the proposed system the boundary extraction is achieved as well as the object segmentation is achieved with the help of Poincare map method within the dynamical system. This method of boundary extraction and image segmentation is more efficient as compared to the traditional ACM’s. In this first the ISAF field is generated for the observed image which it generates a swirling component which acts as the limit cycles in dynamical system corresponding to the desired object.

Then a Poincare section and a Poincare map is generated for the generated ISAF field and the newton-raphson method is used to locate limit cycles and in the end the boundaries of the object are represented by integral equation. The system also achieves multiple boundary extraction by locating some initial points in the generated vector field. And again generating the Poincare map for each point and the newton-raphson will calculate the fixed point for the Poincare map on the object boundary. And then points are liked using the integral formula and extracting the edges on which they lie.

It can be the future scope of the method when the method is extended to 3-D object segmentation.

ACKNOWLEDGMENT

At the outset, I thank the Lord almighty for the grace, strength and hope to make my endeavor a success. I also express my gratitude to Prof. S. M. Rokade, Head of Department for his 9constant support and valuable suggestions without which the successful completion of this work would not have been possible. I specially thank Prof S. D. Jondhale my guide for his boundless cooperation and help extended for this work. I thank all others, and especially my classmates, friends and my family members who on or the other way helped me in the successful completion of this work.

References

M. Kass, A. Witkin, and D.Terzopoulos, “Snakes: Active contour models,” Int. J. Comput. Vis., vol.1, pp. 321–331,1987.
S. Osher and J. A. Sethian, “Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations,” J. Comput. Phys., vol. 79, no. 1, pp. 12–49, Nov. 1988.
V. Caselles, R. Kimmel, and G. Sapiro, “Geodesic active contours,” Int. J. Comput. Vis., vol. 22, no. 1, pp. 61–79, Feb./Mar. 1997.
C. Xu and J. L. Prince, “Snake, shapes and gradient vector flow,” IEEE Trans. Image Process., vol. 7, no. 3, pp. 359–369, Mar. 1998.
C. Xu and J. L. Prince, “Generalized gradient vector flow external forces for active contours,” Signal Process., vol. 71, no. 2, pp. 131–139, Dec. 1998.R. Nicole, “Title of paper with only first word capitalized,” J. Name Stand. Abbrev., in press.
N. Paragios and R. Deriche, “Geodesic active contours and level sets for the detection and tracking of moving objects,” IEEE Trans. Pattern Anal. ach. Intell., vol. 22, no. 3, pp. 266–280, Mar. 2000.
T. F. Chan and L. A. Vese, “Active contours without edges,” IEEE Trans. Image Process., vol. 10, no. 2, pp. 266–277, Feb. 2001
M. Gastaud, M. Barlaud, and G. Aubert, “Combining shape prior and statistical features for active contour segmentation,” IEEE Trans Circuits Syst. Video Technol., vol. 14, no. 5, pp. 726–734, May 2004.
B. Li and S. T. Acton, “Active contour external force using vector field convolution for image segmentation,” IEEE Trans. Image Process., vol.16, no. 8, pp. 2096–2106, Aug. 2007.M. Young, The Technical Writer’s Handbook. Mill Valley, CA: University Science, 1989.