Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580 Biya Motto Frederic1*, Ndzana Benoit2, and Asonganyi Defang Nkafu Austin3
1University of Yaoundé I, Science Faculty, Department of Physics, PO BOX: 812, Cameroon.
2Natioinal Advanced School of Engineering of Yaoundé, Electrical and Telecommunications Department, ACL Laboratory, P O BOX: 8390, Cameroon.
3Mekin Hydroelectric Development Corporation (HYDRO-MEKIN) P. O. BOX: 13155 Yaoundé – Cameroon.
Received: 27/05/2013; Revised: 22/06/2013; Accepted: 04/07/2013
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
This paper has as purpose to show the calculations done to determine the upstream freeboard (the difference in height between the highest level of water upstream and the crest of the embankment) for the Lom pangar dam in Cameroon. The submersion of an embankment due to waves could affect its lifespan and it is thus necessary to verify the height of the crest of the dam in a way that would protect it against a maximum increase of the water level.
freeboard, wind setup, fetch, wave run-up.
Lom Pangar is situated at the confluence of the Lom and Pangar Rivers in the Eastern Region of Cameroon about 420 km east of capital city Yaoundé. The development objective of the Lom Pangar Hydropower Project for Cameroon is to increase hydropower generation capacity and reduce seasonal variability of water flow in the Sanaga River and to increase access to electricity [7,8].
The objective of evaluating the freeboard is to provide needed assurance against overtopping resulting from the following: wind set-up and wave run-up, settlement, landslide and seismic motion, malfunction of some structures and other uncertainties in design construction and operation.Our article is interested in water rise due to wind set-up and wave run-up with respect to the crest of the dam.
The calculation of the freeboard in these situations must take into account two phenomena:
- The increase in water level due to wind (wind set-up), a phenomenon similar to that of tides,
- The appearance of waves generated by wind in deep water where h/L > 0.5, with h being the depth of the water and L the wavelength of the waves.
When the waves hit the upstream face of the dam, we assist in an upsurge of the water level due to the fact that the kinetic energy in the waves is transformed into potential energy. This increase in the height of the waves is called wave run-up.
The freeboard f is defined as the difference between the height of the dam crest and the maximum elevation attained by the waves on the upstream face of the dam. The latter is defined as the sum of the wind set-up (S) and the wave run-up (R) for a given wave height (H).
Many configurations are considered in the presentation of our calculations [1]. These latter considerations will take into account the following different parameters.
- Period of flood returns
- Intensity of the wind blowing in the reservoir
- Number of sluice gates that are open.
Figure 1: A model of the phenomenon caused by wind
The table below shows thedifferent configurations studied in the case of the embankment dam.
Table 1: The calculation of minimum freeboard for the embankment dam
The basic parameters necessary for the evaluation of the minimum freeboard are as follows:
- The fetch,
- The wind speed
The fetch represents the distance which separates the dam from the shore where the wind is blowing. The notion of effective fetch has been introduced to take into account the following phenomena:
- The wind direction which, in most cases, is unknown,
- The border of the reservoir is irregular.
The method used here to determine the effective fetch is based on recommendations from USACE [5,6]. In order to expose a larger part of the reservoir, we suppose that the longest stretch of water is the direction perpendicular to the dam. This length is called the effective fetch and denoted Fe.
The effective fetch method supposes that a directional diffusion of the wind in cosine from the 10th power, starting from the maximum frequency of the wave spectrum and taking into account the distance Fi which separates the border of the damevery 100.
The effective fetch is thus calculated as follows:
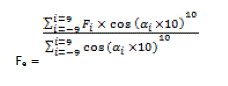eq 1
Fi : the distance separating the border of the reservoir of the dam associated to angle αi.
αi the entireangles associated to the distance Fi (αi = -9, -8, …,0,1,2,…,8,9)
The effective fetch has been calculated for a point on the centre of the dam.
Table 2: Distance to the dam - reservoir and the calculation of the effective fetch
Not having any data on the wind speed on site of dam, a minimum wind speed value of 80km/h on earth recommended by the USBR [4] has been adopted. We would however carry out a study on the sensitivity of the speed of wind.
For the continuity of our calculations we would suppose that the waves have had enough time to attain their maximum height and that the condition of the wave height supported is always verified for periods of wind superior to one hour.
The calculation for the height of the wave depends on the hypothesis of great depth which says that 99% of the energy transported by the wave is concentrated on a height of water at the point Lw/2 where Lw is the wavelength.
The freeboard is calculated by a method integrating the different parameters such as:
- The speed of wind on water at theproject site,
- The nature of the dam: a dam supports a wave run-up depending on how it is compacted,
- The slope and roughness for the upstream face of the dam,
- The value of the effective fetch.
The height of the wave is defined as a function of the wind speed and the effective Fetch.
The following formulas are based on the recommendations of the USACE [4]:
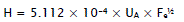eq 2
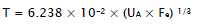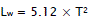eq 3
eq 3
With:
UA wind factor defined as follows: UA = 0.71× (Vw)1.23 [m.s-1]
Hs Significant height of wave [m]
T Wave period [s]
Fe effective fetch [m]
Vw windspeed defined 25 foot above water stretch [m.s-1]
Lw Wave length in deep water [m]
The waves generated by the wind under the hypothesis of great depth do not have the same height. Measures carried out in the sea and in the reservoir during tempests have shown that the characteristics of the wave spectrum are as follows:
H is defined as the average height of waves over the percentage of the highest waves. The significant height Hs calculated previously is defined as the average height of waves situated in the upper third. As we can see in table 3, thirteen percent of the waves go above this height. Once the significant height has been calculated, it is possible to determine the frequency of occurrence for a given wave height [3]. Historically, we usually work with the significant height.
Table 3: Characteristics of wave spectrum
The average of rise in water level is a result of the blowing of the wind. The value of the rise in water level is calculated by applying the Zuider Zee formula (Fell et al., 1992 [2]) as shown below:
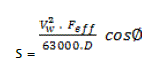eq5
With:
Vw wind speed [Km/h]
Feff effective fetch [Km]
φ Theangle which makes the line with the direction of wind [0]
D Average depth of the reservoir along the fetch line [m]
When Zreservoiris 674.5 m Cameroon geographic Level (CGL), the height of the water at toe of the dam is about 45m. An average depth of 30m has been retained in the ensuing calculations.
The impact height of a wave is a combination of an upsurge in water level and run-up height R associated to a wave height H in deep water.
The relationship R/H can be determined by means of the abacus of figure 2 (Fell et al., 1992 [2]), which permit us to distinguish the upstream slopes having a riprap thus provoking a greater dissipation ofenergy (present case) of impermeable slopes or weakly permeable slopes (slopes made with earth and deprived of upstream protection).
Figure 2: Determining the wave run-up height
For the same slope and the same downstream facing, the different values of the ratio R/H corresponding to different values which the ratio H/Lw can take.
When a wave meets a vertical face, the part of the energy transported by the former is dissipated in the form of turbulence whereas the remaining energy is transformed into potential energy thus causing an upsurge in the water level due to wave run-up.
The expression for the limit angle βof the breaking of the waves on an impermeable face is given by Iribarren and Nogales [3] (1949):
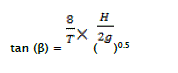eq7
The maximum elevation of the water level at the neighborhood of the upstream face is defined by the following formula:
f = S + R eq8
Where:
S is the wind set-up [m]
R is the wave run-up [m]
A sensibility study has been carried out for windspeed varying between 80Km/hto 120Km/h
Table 4 and 5 synthesize the results obtained for the laterite backfill embankment as well as the transition rock fill embankment.
Table 4: Laterite Embankment fill at 3.5/1 – calculation of the freeboard
Table 5: Transition embankment at 1.5/1 – Calculation of the freeboard
Table 6 synthesizes the results obtained for the RCC dam.
Table 6: The RCC dam – Calculation of freeboard
For each of the configurations considered, the criteria for expected minimum freeboard in table 1 are respected for all the dams considered.
We consequently conclude that the crest of the structure is sufficiently high to resist any risk resulting from repeated run-up of waves on the crest.