ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
A.Angelin1, B. Revathi2, T.Gayathri3, Mr.D.Balakumaran4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Wireless sensor network (WSN) consists of large number of small sensor nodes to monitor physical or environmental conditions. The WSN depends on two major criteria: reliability of links and power consumption. Power supply in sensor nodes are often battery powered. Hence frequent service or sometimes replacement of sensor nodes is necessary. Error correction codes (ECC) is an efficient method to minimize the transmitted power. For the minimization of the power consumption of sensor nodes and to increase the lifetime of nodes, a systematic approach in finding suitable error correction codes for wireless sensor networks is followed in this paper. Suitable error correction code is chosen based on the BER (Bit Error Rate) and power consumption. The ECC provides coding gain which results in energy conservation during transmission.
Keywords |
||||||||
| Error Control Codes, wireless sensor networks, bit error rate, signal to noise ratio, power consumption. | ||||||||
INTRODUCTION |
||||||||
| The development of wireless sensor networks have achieved to great heights due to the development of wireless communication systems, signal processing and digital electronics. The primary operations of the wireless sensor node are to sense, communicate and process [2], [5], [7]. The sensor nodes operate at four different modes which includes transmit state, receive state, idle state and sleep state. Even though there is a wide advancement in sensor networks, the major drawback of WSN is the overwhelming power consumption of the sensor nodes. The higher power consumption of sensor nodes results in the minimization of lifetime of the sensor node. It leads to the periodic replacement of the battery which is not an easy in case of WSN. The power consumption during communicating is significantly higher compared to the power consumption during sensing and processing. The power consumption during receive and idle state is relatively equal. While the sleep state, consumes significant amount of power when changing to transmit state. Channel impairments are caused due to the random noise and fading in the signal [5], [9]. The data which is corrupted, is either discarded and waits for transmission or uses Automatic Repeat request (ARQ) – which request retransmission on the receipt of the negative acknowledge (NACK). In this the energy is wasted in the network. One method of minimizing the power consumption in wireless sensor network is to use error control codes [2]. The forward error correction code is classified into two types: Block codes and Convolutional codes. | ||||||||
| The block code has k input bits and n output bits. When k bits are given as input then it forms 2k distinct messages. Hamming codes, Golay codes are some of the examples of block codes. In most of the applications convolutional codes are used. Applications like satellite and mobile communications, digital video use convolutional codes. Convolutional codes use memory registers. Turbo codes are the hybrid codes. Better performance is obtained on stronger codes with lower power requirements. It also requires complex decoders which consume high power. When the power consumption in the decoder is greater than the transmit power conservation, it would not be a well-organized method for energy conservation. However in case of turbo codes, we consider that decoding is done at the base station where there is no necessity of power utilization since the base station is equipped with enormous amount of power supply | ||||||||
CHANNEL CODING |
||||||||
| Channel coding [16] involves transformation of signal for the better communication performance Channel error correction codes is classified into two types 1. Backward Error Correction codes 2.Forward Error Correction codes. Backward Error Correction codes [19] are also known as Automatic Relay reQuest (ARQ). It uses a feedback from the destination to the source. Although ARQ is simple, there are some of the drawbacks. It increases the delay because it requires acknowledgement for the data that has been sent and delay exceeds if the retransmission requires. It performs better for smaller average packet error rate and it requires FEC for better performance. Applications of ARQ include LANs and transmission of data. | ||||||||
| FEC are of two types: block codes and convolutional codes. Linear block codes [16] has two properties 1. The zero vector is always a codeword 2. The sum of the any two codeword is also a codeword. It transforms a block of messages into longer sequences. The cyclic codes [16] are the subclasses of block codes. Feedback shift registers are used in implementing cyclic codes. The cyclic code follows the two properties: 1.cyclic property and linearity property. Convolutional codes operate on bit streams of arbitrary length. Viterbi algorithm is often used for decoding convolutional codes. Coding gain which is obtained by using error correction codes is defined as the difference between the SNR values of coded and uncoded system to achieve the same bit error rate. In this paper, we use four codes: hamming codes, golay code, RS code and turbo codes. Hamming codes are the classes of block codes. They are perfect codes with the error probability [16] | ||||||||
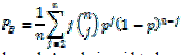 (1) (1) |
||||||||
| where p is the symbol error probability of the channel. A code is said to be perfect codes if it satisfies the hamming bound. Hamming bound [23] states that if C is the codeword of length n and d is the distance then, | ||||||||
| If n≠1 and d ≠1, then there exists a linear code C of length n and distance d with | ||||||||
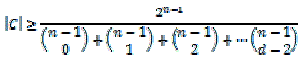 (3) (3) |
||||||||
| This is known as Gilbert-Varshamov bound [23]. Extended golay codes [16] are more efficient than hamming codes. These codes are also perfect codes. It has the minimum distance dmin of 8 and the code rate . The extended golay codes can correct up to triple errors and the bit error rate probability is given as [16] | ||||||||
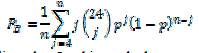 (4) (4) |
||||||||
| Reed-Solomon (RS) [16] are non-binary cyclic codes. It achieves the largest possible code minimum distance for any linear code. RS codes are useful for burst error detection and for channels that have memory. The bit error rate probability of RS code is given as | ||||||||
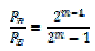 (5) (5) |
||||||||
| Designing an error correction code is always a tradeoff between energy and band-width efficiency. More errors are corrected by using lower rate codes. The system operates with a lower transmit power, when more error is corrected. But the lower code rate codes have excess of overhead and thus there is large bandwidth consumption. It also increases the decoding complexity [20]. | ||||||||
| Turbo codes [20] are the hybrid codes that have been developed for block codes and convolutional codes. Turbo codes are formed by the concatenating two encoders in parallel shown in figure 1. The two encoders are separated by the interleaver. The decoding techniques of turbo codes are MAP (Maximum a Priori) by BCJR and SOVA (Soft Output Viterbi Algorithm) which loses roughly around .7dB coding gain. | ||||||||
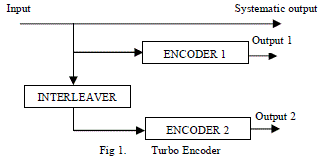 |
||||||||
OPTIMAL CODE SELECTION |
||||||||
| In this paper, we select the optimal code among the specified four codes. The block diagram is shown in figure 2. [1] The selection of error control codes depends on the specific applications. Various modulation techniques (e.g. BPSK,QPSK, MPSK, QAM, OQPSK etc) used is also considered while selecting the ECC. It also depends upon other sensor network constraints such as environmental conditions, channel fading, distance, and number of nodes used [4], [15]. The energy optimal ECC-modulation pair selected for various applications gain 50% of energy [4]. A maximum bit error rate (BER) to obtain quality of Service (QoS) is specified for every applications [14]. Error control codes are used to reduce the bit error rate within the limit. ECC also minimizes the energy while transmitting due to the coding gain. Based on the application, ECC and modulation are selected in the format selector. Energy of a single sensor node is calculated in the energy of the node block. In the energy simulation block, the energy consumed by the network is calculated. This process is repeated until the optimal ECC is selected. Finally we get the system with optimal energy which helps to increase the life time of the network. | ||||||||
| In this paper, we have considered various ECC performance evaluations in terms of their Bit Error rate versus signal to noise ratio curves all using BPSK modulation technique under additive white Gaussian channel noise (AWGN). | ||||||||
ENERGY MODELS |
||||||||
| A. Energy of the Sensor node | ||||||||
| The energy consumption of the sensor node deals with the two energy models [3]: 1. Radio energy model and 2. Computation energy model. In the radio energy model energy is consumed for the circuit and for transmitting the signal. The radio energy model per bit in transmitting M number of bits is given as [3] | ||||||||
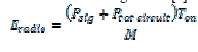 (6) (6) |
||||||||
| Where, | ||||||||
| : power consumed while transmitting the signal. | ||||||||
| power consumed by the circuit. | ||||||||
| duration for which the transceiver is ON | ||||||||
| The power required for transmitting the signal is expressed in Proakis [10] as follows | ||||||||
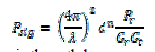 (7) (7) |
||||||||
| Where is the wavelength; is the distance; n is the path loss componet; is the received power; is the antenna gain of the receiver and is the antenna gain of the transmitter. The power consumed by total circuit is given by [3] | ||||||||
| Computation energy model deals with the energy consumed during the encoding and decoding process of various ECC. Consider is the energy consumed during the encoding and is the energy consumed during decoding, then the computational energy model per bit is given as [3]. | ||||||||
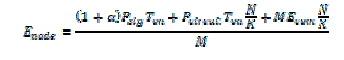 (9) (9) |
||||||||
| The sensor node energy per bit is the addition of the computation energy model and the radio energy model and is given as [3] | ||||||||
| B. Energy of the Network | ||||||||
| In cases like turbo codes where the transmitter energy is reduced considerably with the increase in the complexity of the decoder, we consider that the decoding is done at the base station where there is no scarcity of energy. The energy consumed by the overall sensor network is given by [2]. | ||||||||
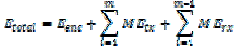 (11) (11) |
||||||||
| is the total energy of the network; Eenc is the encoding energy of the node; E(TX )is the transmitting energy of all the sensor nodes; ERX is the receiving energy of all the nodes[2]. | ||||||||
| Where M is the total number of bits that has been transmitted; energy consumed for a single bit transmission from the node; energy consumed for a single bit reception by the node. | ||||||||
SIMULATION ENVIRONMENT |
||||||||
| Network simulator version 2 (NS2) [21] is used to calculate the energy consumption of the sensor node and the energy consumption of the wireless sensor network. NS2 is used because it can evaluate the performance of the network and scale the protocols before they are being used. It also provides the environment to run large scale experiments which cannot be implemented in real experiments. The simulator is written in C++ and uses OTcl interpreter as the front end. The graphs shown in the fig 3, 4 are the performance evaluation of bit error rate to signal to noise ratio for various error correction codes are obtained using MATLAB. Suitable error correction code is chosen systematically based on the limits of BER (Bit Error Rate) for various application and power consumption. The various parameters for the simulation of energy consumption of the sensor node and the energy consumption of the network is shown in table I [1], [4] | ||||||||
| The comparison between the coded system using various ECCs and the uncoded system is done. In fig 3. it shows the performance of various ECCs that involves hamming codes, extended Golay codes and Reed Solomon codes in terms of bit error rate. In fig 4. the RS codes performance was simulated for various code rates [1], [2]. From fig 3. [1], [2] it shows that RS codes perform better than the Golay codes and hamming codes. The coding gain of the hamming code is of 1.4dB. From [25] it is clear that the turbo codes solve the problem of energy consumption by coding gain that saves the transmitter’s energy. | ||||||||
CONCLUSION |
||||||||
| One of the major constraints of wireless sensor network is the power consumption. Since the WSN is often battery powered and located in areas where the replacement of the nodes is quite difficult, minimization of the power utilization is necessary. ECC helps to minimize the power utilization using the coding gain. Since turbo codes have more complex decoder, we consider that the decoding is done at the base station [2]. Base station has surplus amount of power supply hence there is no need of power conservation. Moreover the decoding techniques of turbo codes with the low complexity decoder for WSN have been explained in [22]. Hence turbo codes are efficient compared to other codes. | ||||||||
Tables at a glance |
||||||||
|
||||||||
Figures at a glance |
||||||||
|
||||||||
References |
||||||||
|