ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
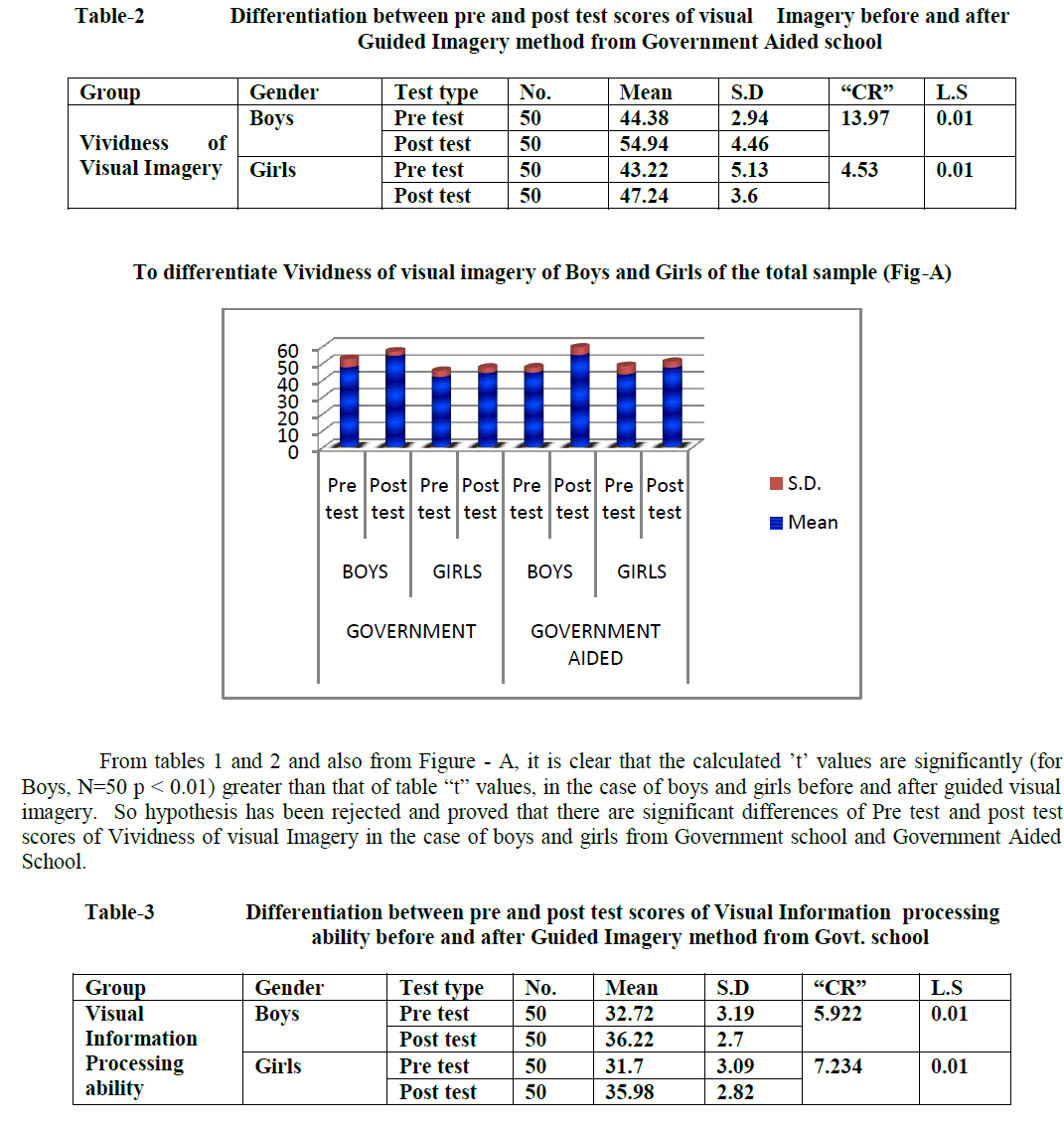
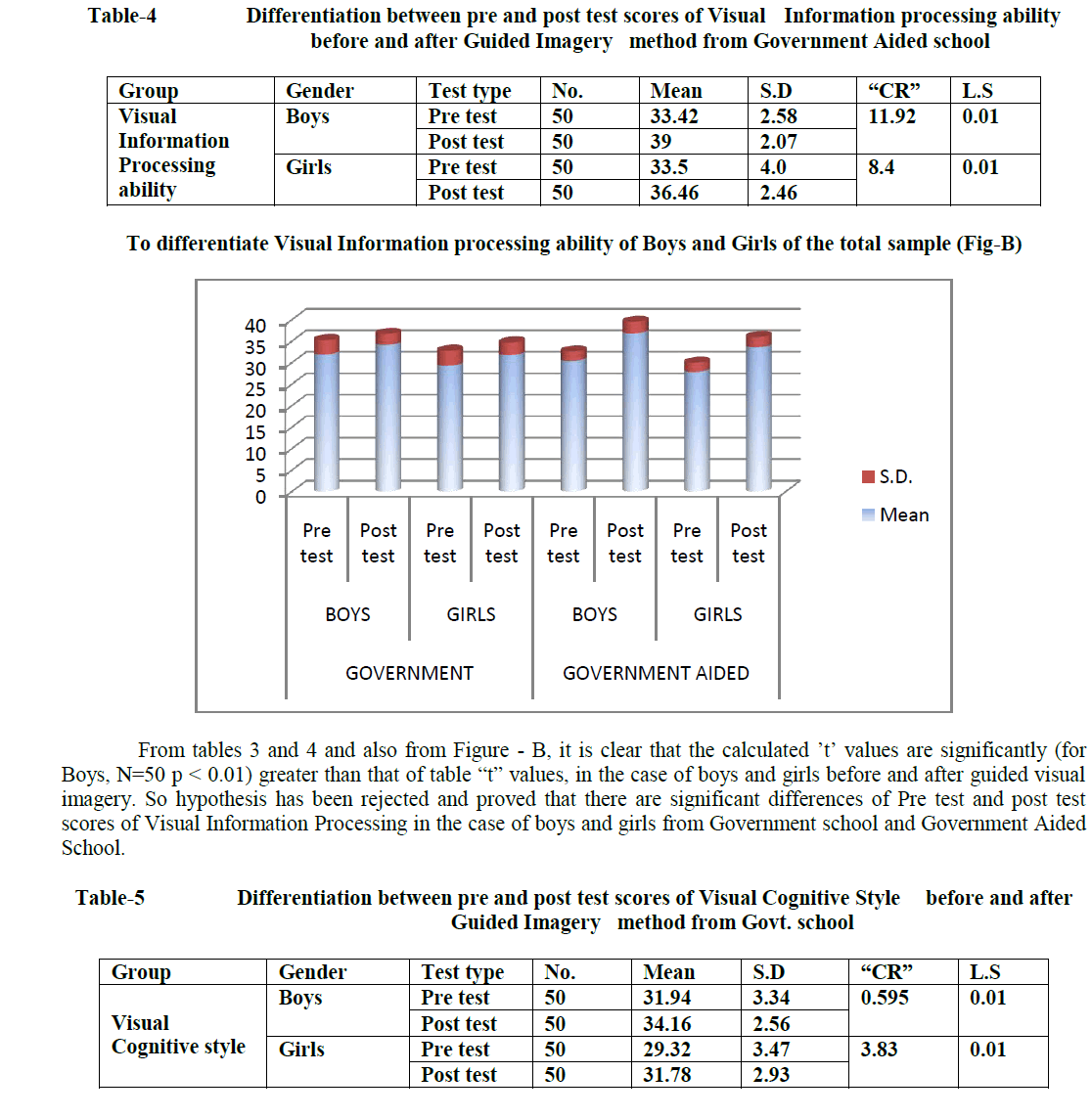
| C.Lavanya, M.Nandihini, R.Niranjana, C.Gunavathi Computer Science and Engineering, K.S.Rangasamy College of Technology, Tiruchengode, Tamilnadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Genes are encoding regions that form necessary building block inside the cell and show the way to proteins which are achieving a variety of functions. However, some genes may get mutated. Such genes are responsible for cancer occurrence. It can be discovered by closely examining samples taken from patients to identify faulty genes. Gene expression dataset usually comes with only dozens of tissues/samples but with thousands or even tens of thousands of genes/features. In this paper, we employ feature selection techniques for analyzing cancer microarray gene expression data. Feature selection technique is used to select the most possibly cancerrelated genes from huge microarray gene expression data. It aims to achieve improved classification performance. This can be achieved by the measures of T-Test, Chi-Square Test and Information gain. Cancer classification using microarray data poses another major challenge because of the huge number of genes compared to the number of tissue samples. Only a small number of genes in the microarray data which consisting of thousands of genes show strong correlation with the target phenotypes. This paper presents the Naive Bayes algorithm for the classification task. A comprehensive framework that incorporates feature selection and classification techniques is capable of successfully classifying new samples as infected or normal
Keywords |
| Gene Expression Data, Classification, Feature selection method, Naive Bayes algorithm |
INTRODUCTION |
| Data mining is the computational process of analysis of large quantities of data. It uses information from past data to analyze the outcome of a particular problem or situation that may arise. Data classification is the form of data analysis that extracts models of describing important data classes. Such models called classifiers, predict categorical class labels. Such analysis can help us with better understanding of data at large. The class label of each training label is provided a state called supervised learning that is the learning of the classifier of supervised in that it is told to a class each training tuple belong. In learning, training data are analyzed by classification algorithm in which test data are used to estimate the accuracy of classification rules. |
BASICS OF GENE EXPRESSION DATA |
| Gene expression is the process by which information from a gene is used in the synthesis of a functional gene product. These products are often proteins, but in non protein coding genes such as rRNA genes or tRNA genes, product is a structural or housekeeping RNA. Gene expression studies can also involve looking at profile or patterns of expression of several genes whether quantitating changes in expression levels or looking at overall patterns of expression, real time PCR is used by most scientists performing gene expression. Based on the levels of the gene expression data optimized genes are classified based on different classifiers. |
MICROARRAY DATA CLASSSIFICATION |
| The micro array data are images, which have to be transformed into gene expression matrices in which rows represent genes, columns represent various samples such as tissues or experimental conditions, and numbers in each cell characterizes the expression level of particular gene in the particular sample. Microarray based disease classification system takes labeled gene expression data samples and generates a classifier model that classifies new data samples into different predefined diseases. Microarray data classification is a supervised leaning task that predicts the diagnostic category of a sample from its expression array phenotype. |
 |
GENE EXPRESSION DATA SETS |
| The datasets considered in the simulation are Iris, yeast, Spellman dataset, breast cancer. All these data sets are publicly available and are two class gene expression |
 |
GENE SELECTION |
| In this study, a number of gene selection methods have been introduced to select informative genes. The different dataset genes are classified using classifier like SVM, Naive Bayesian and optimized genes obtained through feature selection methods like TTest, information gain and mutual information. |
FEATURE SELECTION METHODS |
| The importance of feature selection methods is selecting informative genes prior to classification of microarray data for cancer prediction and diagnosis. Feature selection method removes irrelevant and redundant features to improve classification accuracy. Feature selection methods can be categorized into filter, wrapper, and embedded or hybrid. The filter approach selects features without involving any data-mining algorithm. The filter algorithms are evaluated based on four different evaluation criteria namely, distance, information, dependency and consistency. The wrapper approach selects feature subset based on the classifier and ranks feature subset using predictive accuracy or cluster goodness. It is more computationally expensive than the filter model. |
T –TEST |
| To measure the relevance of a gene, the t-test is widely used, assuming that there are two classes of samples in a gene expression data set. When there are multiple classes of samples, the t-test is computed for one class versus all the other classes. It compares the actual difference between two means in relation to the variation in the data. T Test values are calculated as |
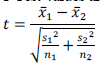 |
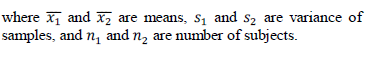 |
CHI-SQUARE TEST |
| Chi-square is a statistical test commonly used to compare observed data with data we would expect to obtain according to a specific hypothesis. This is designed specifically for multiple tests having at least two discrete outcomes (such as normal and mutated gene). The chi-square test is always testing what scientists call the null hypothesis, which states that there is no significant difference between the expected and observed result. The formula for calculating chi-square (x2) is: |
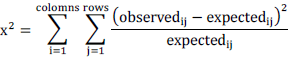 |
| A Chi Square Test is often used to measure a goodness of fit between an observed and expected distribution of values knowing how to perform a Chi Square test can be useful for testing probable to expected outcomes, fitting points to a curve, or testing a statistical hypothesis. |
INFORMATION GAIN |
| Information gain, of a term measures the number of bits of information obtained for category prediction by the presence or absence of the term in a document. Information Gain measures the decrease in entropy when the feature given is absent. This is the application of a more general technique, the measurement of informational entropy, to the problem of deciding how important a given feature is. Informational entropy, when measured using Shannon entropy, is notionally the number of bits of data it would take to encode a given piece of information. The more space a piece of information takes to encode, the more entropy it has. Intuitively, this makes sense because a random string has maximum entropy and cannot be compressed, while a highly ordered string can be written with a brief description of the string’s information. In the context of classification, the distribution of instances among classes is the information in question. If the instances are randomly assigned among the classes, the number of bits necessary to encode this class distribution is high, because each instance would need to be enumerated. |
| On the other hand, if all the instances are in a single class, the entropy would be lower, because the bitstring would simply say “All instances save for these few are in the first class.” Therefore function measuring entropy must increase when the class distribution gets more spread out and be able to be applied recursively to permit finding the entropy of subsets of the data. The following formula satisfies both of these requirements: |
| IG(X) = H(D)− H(D|X) where |
| H(D) = - Σ (ni/n) log(ni/n) i=1,…l and |
| H(D|X) = - Σ (|Xj|/n)H(D|X-Xj) |
| p±(S) is the probability of a training example in the set S to be of the positive/ negative class. We discretized continuous features using information theoretic binning. |
| For each dataset we selected the subset of features with non-zero information gain. Information Gain can be used only on discrete features and hence for numeric features discretization is necessary prior to computing Information Gain. Entropy-based discretization method is generally used for gene expression data. Similar, to t-Statistic, features are selected based on the larger values of Information Gain. |
CLASSIFIERS |
NAIVE BAYES CLASSIFIER |
| A Naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model". In simple terms, a naive Bayes classifier assumes that the presence or absence of a particular feature is unrelated to the presence or absence of any other feature, given the class variable. Naive Bayes is that it only requires a small amount of training data to estimate the parameters (means and variances of the variables) necessary for classification. Because independent variables are assumed, only the variances of the variables for each class need to be determined and not the entire covariance matrix. |
DISCUSSION AND CONCLUSION |
| We showed how combining a filtering technique for feature selection with SVM leads to substantial improvement in generalization performance of the SVM models in the five classification datasets of the competition. Another lesson learned from our submission is that there is no single best feature selection technique across all five datasets. We experimented with different feature selection techniques and picked the best one for each dataset. Of course, an open question still remains: why exactly these techniques worked well together with Support Vector Machines. A theoretical foundation for the latter is an interesting topic for future work. |
References |
|