ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| A.Ashok kumar1, Dr.P.Vivekanandan2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Complex networks, such as biological, social, and communication networks, often entail uncertainty, and thus, can be modelled as probabilistic graphs. In a clustering problem one has to partition a set of elements into homogeneous and well-separated subsets. From a graph theoretic point of view, a cluster graph is a vertex-disjoint union of cliques. The clustering problem is the task of making fewest changes to the edge set of an input graph so that it becomes a cluster graph. Problems of Probabilistic Graph Clustering are Similar to the problem of clustering standard graphs. Probabilistic graph clustering has numerous applications, such as finding complexes in probabilistic protein-protein interaction (PPI) networks and discovering groups of users in affiliation networks. The Probabilistic Graph is generated using the Probability of occurrence of the nodes in the affiliated network. Deterministic Graph is generated depending upon the active nodes in affiliated network. The proposed system establishes a connection between our objective function and correlation clustering to propose practical approximation algorithms for Probabilistic Graph problem. A benefit of proposed approach is that the objective function is parameter-free. Therefore, the number of clusters is part of the output. The Proposed method discovers the correct number of clusters and identifies established protein relationships.
INTRODUCTION |
| There is a growing awareness of the need for database systems to be able to handle and correctly process data with uncertainty. Conventional systems and query processing tools are built on the assumption of precise values being known for every attribute of every tuple. But any real dataset has missing values, data quality issues, rounded values and items which do not quite fit any of the intended options. Any real world measurements, such as those arising from sensor networks, have inherent uncertainty around the reported value. Other uncertainty can arise from combination of data values, such as record linkage across multiple data sources and from intermediate analysis of the data Given such motivations, Research is ongoing into how represent, manage, and process data with uncertainty. |
| One of the methods for finding clusters in the uncertain database is probabilistic graph clustering. This paper focuses on the problem of partitioning a probabilistic graph into clusters. The Proposed system treats every probabilistic graph G as a generative model for deterministic graphs. Each such deterministic graph is a possible world of G and is associated with a probability to be generated. Consider a deterministic graph G =(V,E) and a partitioning, C, of the nodes in V. A clustering objective function D(G,C) quantifies the cost of the clustering C with respect to G. The possible-world semantics dictate that the cost of a clustering C for a probabilistic graph G is the expected value of D(G,C), over all possible worlds of G (i.e., D(G, C) = E[D(G,C)]). Although this generalization is natural, it raises computational concerns. For instance, evaluating D(G, C) using the definition of expectation requires considering all, exponentially many, possible worlds of G. Further, the expectation of well-established clustering objective functions(e.g., the maximum cluster diameter), is infinite since, typically, there exist possible worlds where parts of the graph are disconnected. Therefore, new definitions of the clustering problem in probabilistic graphs are necessary. |
| We view clustering C as a cluster graph, i.e., a graph consisting of disconnected cliques. Our optimization function is the edit distance between G and cluster graph C. In other words, D(G,C) is the number of edges that we need to add and remove from G to get C. Given a probabilistic graph G, we define PCLUSTEREDIT as the problem of finding the cluster graph C that has the minimum expected edit distance from G. Our problem is a generalization of the CLUSTEREDIT problem introduced by Shamir et al for deterministic graphs. |
RELATED WORK |
| To the best of our knowledge, we are the first to define and study the problem of clustering probabilistic graphs using the possible-worlds semantics. However, uncertain data management and graph mining has motivated many studies in the data mining and database community. We highlight some of this work here. |
| Graph and probabilistic-graph mining. Clustering and partitioning of deterministic graphs has been an active area of research [1]. For an extensive survey on the topic see [4] and the references therein. Most of these algorithms can be used to handle probabilistic graphs, either by considering the edge probabilities as weights, or by setting a threshold value to the probabilities of the edges and ignoring any edge with probability below this threshold. The disadvantage of the first approach is that once probabilities are interpreted as weights, then no other weights can be taken into consideration (unless the probabilities are multiplied with edge weights—in which case this composite weight has no interpretation). The disadvantage of the second approach is that there is no principled way of deciding what the right value of the threshold is. Although both the above methodologies would result in an algorithm that would output some node clustering, this algorithm, contrary to ours, would not optimize an objective defined over all possible worlds of the input probabilistic graph. Further, various graph mining problems have been studied recently assuming uncertain graphs [2]. functions between nodes in probabilistic graphs that extend shortest path distances from deterministic graphs and c proposed methods to compute them efficiently. The problem of finding shortest paths in probabilistic graphs based on transportation networks has also been considered |
| The intersection between the above methods and ours is that all of them deal with probabilistic graphs. However, the graphclustering task under the possible worlds semantics has not yet been addressed by researchers in probabilistic graph mining. Data mining on uncertain data. Data mining over uncertain data has also received a lot of attention. Several classical datamining problems have been revisited in the context of uncertainty. Examples include clustering of relational data frequentpattern mining and evaluating spatial queries [3]. All these works are tailored to model uncertain multidimensional data where uncertainty is associated either with the location of the data points in the space or with the actual existence of the data point in the data set. One could think of defining probabilistic-graph clustering using the same ideas as those used for clustering uncertain multidimensional data. After all, the main idea there is to consider as an objective the expectation of standard clustering optimization criteria across all possible worlds [3]. It may be tempting to try and use the same definitions for probabilistic graphs, particularly since standard clustering objectives (e.g., k-center or k-median)can be optimized in deterministic graphs. However, there is a fundamental difficulty with such clustering definitions in the probabilistic-graph setting: since there are many worlds where parts of the graph are disconnected, the distance (proximity) of a node to any of the existing clustering centers can be infinity. Indeed, for nontrivial probabilistic graphs, there is always a nonzero probability of having a node with infinite distance to all the cluster centers. In that case, the optimization function becomes infinity. Therefore, new definitions of the clustering problem in probabilistic graphs are necessary. This paper addresses this challenge. |
| Probabilistic databases. Probabilistic databases is another active research area, mostly focusing on the development of methods for storing, managing, and querying probabilistic data There exists fundamental work on the complexity of query evaluation on such data [5], on the computation of approximate answers to queries and on efficient evaluation of top-k queries [4]. Although we borrow the possible-world semantics pioneered by the probabilistic-database community. |
PROPOSED METHODOLOGY |
| Probabilistic Graph clustering approach has problem of partitioning a probabilistic graph into clusters. This is a fundamental problem for probabilistic graphs, just it is for deterministic graphs. Partitioning a probabilistic graph into clusters has many applications such as finding complexes in protein-protein interaction networks and communities of users in social networks. A straightforward approach to clustering probabilistic graphs is to heuristically cast the probability of every edge into a weight and apply existing graph clustering algorithms on this weighted graph. This approach is problematic, not only there is no meaningful way to perform such a casting, but also there is no easy way to additionally encode normal weights on the edges. |
| There are many algorithms are used for the cluster identification and edit distance identification in large and uncertain databases. Some of the algorithms are Agglomerative, PCast, Reference, Furthest, Balls. The performance of those algorithms is comparatively lower than the proposed system for finding Edit distance and clusters in the uncertain and large databases.[4]. The disadvantages of existing system are, Probabilities are interpreted as weights, no other weights can be taken into consideration. There is no principled way of deciding what the right value of the threshold. Non zero probability node with infinite distance to all the cluster centers. The optimization function becomes infinity. |
| Clustering Probabilistic Graphs has many desirable features. First Objective function can be computed in polynomial time. The value of our objective function is never infinity. We establish a connection between our problem and correlation clustering. Our algorithms also provide approximation guarantees. Partition of the nodes of the probabilistic graph into groups. |
Algorithm |
| PKwikCluster algorithm |
| The quality of the solutions it produces in terms of both their edit distance and their structural characteristics compare favorably to the other algorithms. |
| Edit distance based |
| Given two deterministic graphs. We define the edit distance between G and Q, to be the number of edges that need to be added or deleted from G in order to be transformed into Q. |
Results |
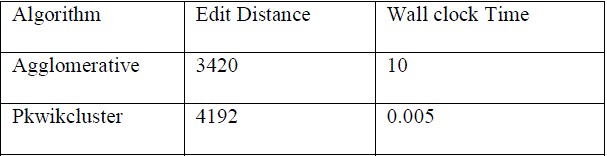
| TABLE 1 CORE Data Set: Summary of Results in Terms of Edit Distance and Wallclock Time of existing and proposed Algorithms. |
 |
| TABLE 2 CORE Data Set: Summary of Clustering Results of existing and proposed Algorithms. |
 |
CONCLUSION |
| It presents a thorough study of clustering probabilistic graphs using the edit distance metric. The main focus is on the problem of finding the cluster graph that minimizes the expected edit distance from the input probabilistic graph. The formulation adheres to the possible- worlds semantics. Also, the objective function does not require the number of clusters as input; the optimal number of clusters is determined algorithmically. The problem here is efficiently approximated, by establishing a connection with correlation clustering. In addition, various intuitive heuristics to address it is being proposed. Further, the framework to compute deviations of a random world to the proposed clustering and to test the significance of the resulting clustering to randomized ones is established. Also, our problem where the output clustering is itself noisy is addressed. The algorithms are tested on a real probabilistic protein-protein interaction network and on a probabilistic social network that we created from Facebook! Groups. The experimental evaluation demonstrated that the algorithms not only produce meaningful clustering with respect to established ground truth, but they also discover the correct number of clusters. Finally, it is demonstrated that they scale to graphs with number of nodes and that they produce statistically significant results. number of clusters. Finally, it is demonstrated that they scale to graphs with number of nodes and that they produce statistically significant results. |
References |
|