International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Common fixed point theorems for self maps on a fuzzy metric space involving integral type in equalities

K.P.R.Sastry1, G.A.Naidu2, N.Umadevi3
 8-28-8/1, Tamil Street, Chinna Waltair, Visakhapatnam-530017, India1
Department of Mathematics, Andhra university, Visakhapatnam-530003, India2
Department of Mathematics, Raghu Engineering College, Visakhapatnam-531 162, India3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Malhotra [7] proved a common fixed point theorem in fuzzy metric spaces for occasionally weakly compatible mappings with integral type in equality by reducing its minimum value. In this paper we prove a common fixed point theorem in fuzzy metric spaces for occasionally weakly compatible mappings with integral type inequality involving some special type of Lebesgue integrable functions.

Keywords
Fuzzy metric space, occasionally weakly compatible (owc) mappings, common fixed point.
Mathematical Subject Classification (2010): 47H10, 54H25

INTRODUCTION
Fuzzy set was introduced by Zadeh [15].Kramosil and Michalek [6] introduced the notion of a fuzzy metric space, George and Veermani [4]modified the notion of fuzzy metric spaces with the help of continuous t-norms. Grabiec[3],Subramanyam[13], Vasuki[14], Pant and Jha [9]obtained some analogous results proved by Balasubramaniam [1] et al. Subsequently, it was developed extensively by many authors and used in various fields. Jungck [5] introduced the notion of compatible maps for a pair of self maps.George and Veermani [4], Sessa [11] initiated the tradition of improving commutative condition in fixed point theorems by introducing the notion of weak commuting property. Further Jungck and Rhoades [5] gave a more generalized condition defined as compatibility in metric spaces. Jungck and Rhoades [5] also introduced the concept of weakly compatible maps.Malhotra [7] proved a common fixed point theorem in fuzzy metric spaces for occasionally weakly compatible mappings with integral type in equality by reducing its minimum value. In this paper we prove a common fixed point theorem for selfmaps on fuzzy metric spaces for occasionally weakly compatible mappings with integral type inequality involving some special type of Lebesgue integrable functions (Definition [2.1]).
Definition 1.1 :( Zadeh.L.A. [14]) A fuzzy set A in a nonempty set X is a function with domain X and values in 0,1 .
Definition 1.2: ( Schweizer.B. and Sklar. A. [9]) A function ∗ ∶ 0,1 × 0,1 → 0,1 is said to be a continuous t-norm if ∗ satisfies the following conditions:
 
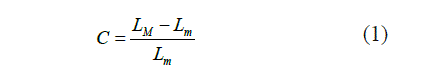Definition 1.3: (Kramosil. I. and Michalek. J. [5]) A triple (X, M,*) is said to be a fuzzy metric space (FM space, briefly) if X is a nonempty set, * is a continuous t-norm and M is a fuzzy set on X2 × [0, ∞) satisfying the following conditions:
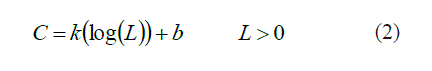Then M is called a fuzzy metric space on X.
The function M(x, y, t) denotes the degree of nearness between x and y with respect to t.
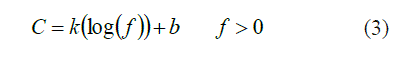Definition 1.6: (George.A. and Veeramani.P. [3]) Let (��, ��,∗) be a fuzzy metric space.
Then,
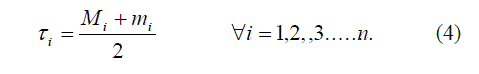Definition 1.7: (Malhotra.S.K.Naveen Verma and Ravindra Sen [6]) Two self maps f and g of a set ��are occasionally weakly compatible (owc) iff there is a point �� in �� which is a coincidence point of �� and �� at which �� and �� commute.
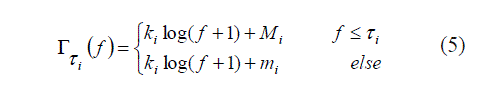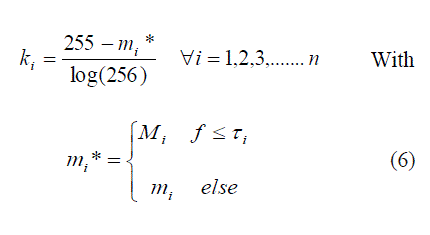Malhotra et.al.[7] proved a common fixed point theorem for four self maps on a fuzzy metric space which satisfy an inequality involving a function ∅ ∈ Φ.
Theorem 1.11: (Malhotra et.al.[7]) Let (��, ��,∗) be a complete fuzzy metric space and let F, G, S and T are self–mapping of X. Let the pairs {F,S} and {G ,T} be owc . If there exists �� ∈ (0,1) such that

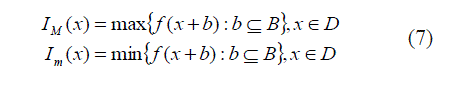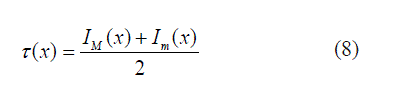II. MAIN RESULT
In this section we introduce a special class of Lebesgue integrable function and use this notion to prove a fixed point theorem.
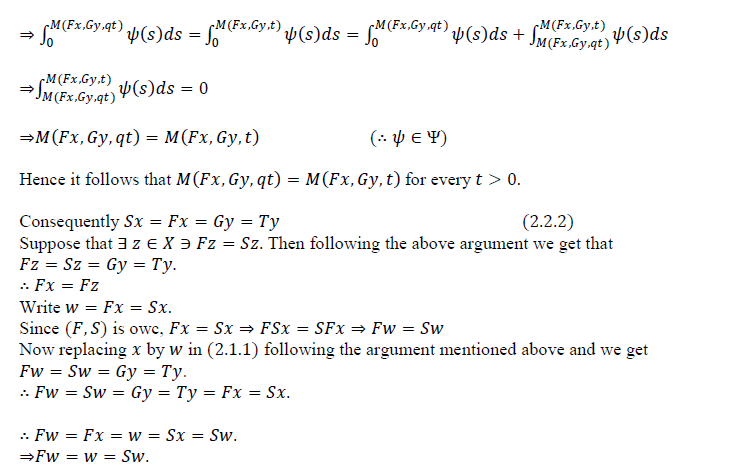Hence �� is a common fixed point of �� and ��. From (2.2.2) we have ���� = ���� = ��,followingthe above argument follows that ���� = ���� = ��. Thus �� is a common fixed point of ��, ��, �� and ��.
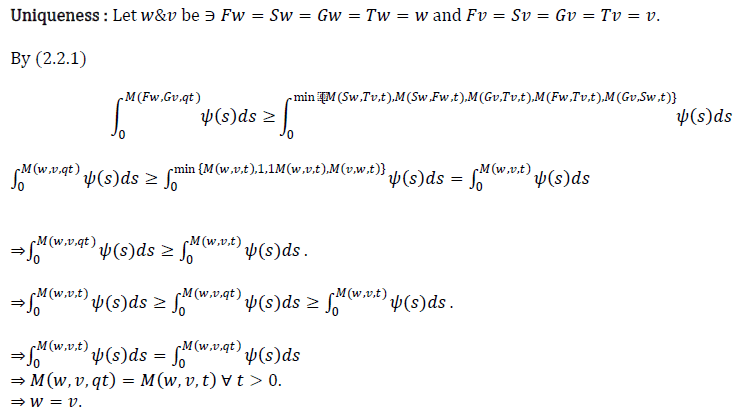Hence common fixed point of F, G, S and T is unique.
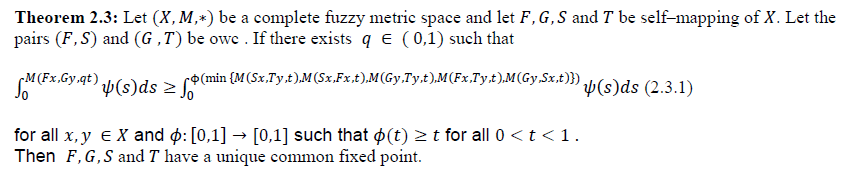Proof : By (2.3.1)
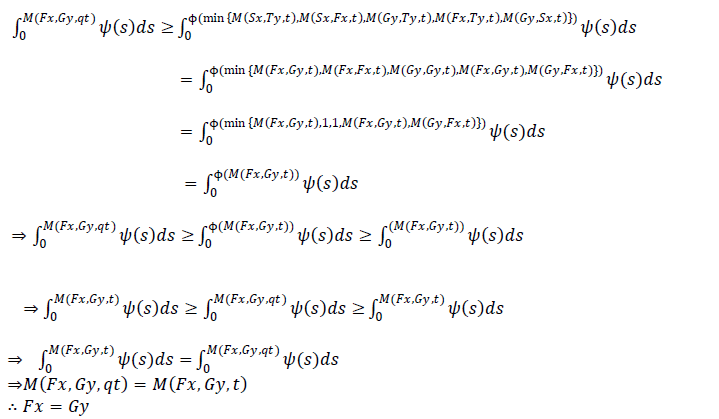Hence result follows from theorem (2.2)
Hence result follows from theorem (2.2)

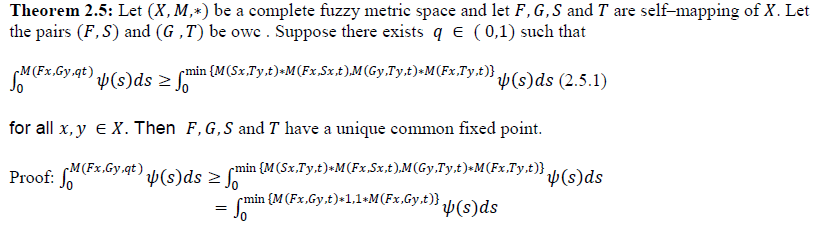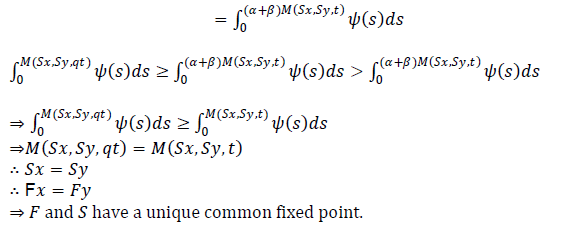ACKNOWLEDGEMENT
The third author (N.U) is grateful to Raghu Engineering College authorities for giving permission and the management of SITAM for giving facilities to carry on this research.
 

References
  1. Balasubramaniam, P., Muralisankar, S., Pant, R.P., Common _xed' points of four mappings in a fuzzy metric space, J. Fuzzy Math., 10(2) (2002), 379-384.
  2. Cho. Y.J. , H.K. Pathak , S.M. Kang , J.S. Jung “Common Fixed Points of compatible maps of type (A) on fuzzy metric spaces” , Fuzzy Sets and Systems 93 (1998), 99-111.
  3. Grabiec .M. “Fixed points in fuzzy metric spaces”, Fuzzy Sets and Systems 27 ( 1988) , 385-389.
  4. George.A and Veeramani.P, On some results in fuzzy metric spaces, Fuzzy Sets and Systems, 64(1994), 395-399.
  5. Jungck.G and Rhoades.B.E, Fixed points for set valued functions without continuity, Indian J. Pure Appl. Math., 29(1998), 227-238.
  6. Kramosil.I and Michalek.J, Fuzzy metric and statistical metric spaces, Ky-bernetika, 11(1975), 336-344.
  7. Malhotra.S.K,Navin Verma,Ravindra Sen, “Occasionally weakly compatible mappings and fixed point theorem in fuzzy metric spaces satisfying integral type inequality.” Internationl journal of statisstika and mathematika,vol2,issue3,2012,pp21-26.
  8. Mishra.S.N, Sharma.N and S. L. Singh, Common fixed point of maps on fuzzy metric spaces, Internat. J. Math. Math. Sci., 17(1994), 253-258.
  9. Pant. R.P., K. Jha, “A remark on common fixed points of four mappings in a fuzzy metric space”, J Fuzzy Math. 12(2) (2004) ,433-437.
  10. Schweizer.B and Sklar.A,Probabilistic Metric Spaces, North Holland, Ams-terdam, 1983.
  11. Sessa.S, “On weak commutativity conditionof mapping in fixed point consideration”. Publ. Inst.Math(Beograd) N.S.,32(46),(1982),149-153.
  12. Singh.B and Jain.S. Weak compatibility and fixed point theorems in fuzzy metric spaces,Ganita, 56(2)(2005), 167-176.
  13. Subramanayam. P.V., “Common fixed points theorem in fuzzy metric spaces”, InformationScience 83(1995) 105-112.
  14. Vasuki.R. “Common fixed points for Rweakly commuting Maps in fuzzy metric spaces”.Indian J .Pure Appl. Math 30 (1999) ,419-423.
  15. Zadeh.L.A, Fuzzy sets, Infor. and Control, 8(1965), 338-353.