Comparative Analysis of Advanced Algorithms for Feature Selection

Abstract

Feature Selection is the preprocessing process of identifying the subset of data from large dimension data. To identifying the required data, using some Feature Selection algorithms. Like ReliefF, Parzen-ReliefF algorithms, it attempts to directly maximize the classification accuracy and naturally reflects the Bayes error in the objective. Proposed algorithmic framework selects a subset of features by minimizing the Bayes error rate estimated by a nonparametric estimator. A set of existing algorithms as well as new ones can be derived naturally from this framework. As an example, we show that the Relief algorithm greedily attempts to minimize the Bayes error estimated by the k-Nearest-Neighbor (kNN) method. This new interpretation insightfully reveals the secret behind the family of margin-based feature selection algorithms and also offers a principled way to establish new alternatives for performance improvement. In particular, by exploiting the proposed framework, we establish the Parzen-Relief (PRelief) algorithm based on Parzen window estimator. The RELIEF algorithm is a popular approach for feature weight estimation. Many extensions of the RELIEF algorithm are developed. Because of the randomicity and the uncertainty of the instances used for calculating the feature weight vector in the RELEIF algorithm, the results will fluctuate with the instances, which lead to poor evaluation accuracy. To solve this problem, a feature selection algorithm parzen+reliefF based algorithm is proposed. It takes both the mean and the variance of the discrimination among instances and weights into account as the criterion of feature weight estimation, which makes the result more stable and accurate. And the main idea is how to estimate the performance of the both algorithms, for this we are using two algorithms for calculating the quality of the generated out puts. They are Leader and sub-leader algorithm and Davies– Bouldin index (DBI) algorithm. Both are clustering algorithms. Which are used for knowing the cluster quality and cluster similarity.

Keywords

Feature Selection; Knn, Parzen, ReliefF

INTRODUCTION

Gauthier et.al [1] said in “Risk Estimation and Feature Selection” For classification problems, the risk is often the criterion to be eventually minimized. It can thus naturally be used to assess the quality of feature subsets in feature selection. However, in practice, the probability of error is often unknown and must be estimated. Also, mutual information is often used as a criterion to assess the quality of feature subsets, since it can be seen as an imperfect proxy for the risk and can be reliably estimated. In this paper, two different ways to estimate the risk using the Kozachenko-Leonenko probability density estimator are proposed. The resulting estimators are compared on feature selection problems with a mutual information estimator based on the same density estimator. Along the line of our previous works, experiments show that using an estimator of either the risk or the mutual information give similar results.

G. Holmes et.al [2] explained that in order to obtain useful results using supervised learning of real-world datasets it is necessary to perform feature subset selection and to perform many experiments using computed aggregates from the most relevant features. It is, therefore, important to look for selection algorithms that work quickly and accurately so that these experiments can be performed in a reasonable length of time, preferably interactively. This paper suggests a method to achieve this using a very simple algorithm that gives good performance across different supervised learning schemes and when compared to one of the most common methods for feature subset selection. Feature subset selection is generally achieved against some form of objective function. In our case we choose classification accuracy as an objective function; our goal being to improve (or not dramatically reduce) classification accuracy while reducing the number of features in the original dataset. The objective function is used by a search strategy to find the “best” subset. If there are d features then the size of the search space of all possible features is 2d. It is not practical to exhaustively search this space and so some form of hill-climbing or optimization technique is used to guide the search. Subsets found using non-exhaustive search strategies do not guarantee to find optimal solutions, and that is the sense in which “best” subsets are found. It is the search strategy that accounts for the cost of performing feature subset selection. This cost and the accuracy of the resulting subset of features are useful measures for comparing the performance of different algorithms.

Peng-Feizhu et.al mentioned in [3] that Feature selection is viewed as an important preprocessing step for pattern recognition, machine learning and data mining. It is used to find an optimal subset to reduce computational cost, increase the classification accuracy and improve result comprehensibility. In this paper, a weighted distance learning approach is introduced to minimize Leaving-One-Out classification error using a gradient descent algorithm. The quality of features is evaluated with the learned weight and the features with great weights are considered to be useful for classification. Experimental analysis shows that the proposed approach has better performance than several state-ofthe art methods. We propose a feature selection technique for nearest neighbor classification via minimizing the leaveone- out NN error estimation of misclassification probability, which is called MLOONNE. Classification error rate measures are called “wrapper methods” and they are employed in . Classification error holds a relationship with predictive accuracy of a classifier, which is often used as a validation criterion, as the sum of predictive accuracy and error rate is 1.Roberto and Enrique in used a fuzzy sigmoid function to approximate the step function to make leaveone- out (LOO) NN error estimation continuous for optimization. In our work, we use the LOONN error estimation as the evaluation function and get a weight vector of features using a gradient decent algorithm. Then features are ranked according to the learned weight vector and features with greater weights are more useful for classification. In essence, we aim to find an optimal feature space in which we can obtain the least LOO NN error estimation, which means the improvement of the overall accuracy and dimension reduction. It is obvious that the proposed technique is one of the filter methods.

Yuxuan SUN et.al said in [4] proposed the RELIEF algorithm is a popular approach for feature weight estimation. Many extensions of them RELIEF algorithm are developed. However, an essential defect in the original RELIEF algorithm has been ignored for years. Because of the randomicity and the uncertainty of the instances used for calculating the feature weight vector in the RELEIF algorithm, the results will fluctuate with the instances, which lead to poor evaluation accuracy. To solve this problem, a novel feature selection algorithm based on Mean-Variance model is proposed. It takes both the mean and the variance of the discrimination among instances into account as the criterion of feature weight estimation, which makes the result more stable and accurate. Based on real seismic signals of ground targets, experiment results indicate that the subsets of feature generated by proposed algorithm have better performance. As a part of any feature selection method, there are several factors that need to be considered, the most important are: the estimation measure and the search strategy.

FEATURE SELECTION

This Discriminative feature selection by non parametric way with cluster validation is advisable to apply to the dataset preprocessing techniques to reduce the number of attributes or the number of examples in such a way as to decrease the computational time cost. These preprocessing techniques are fundamentally oriented to either of the next goals: feature selection (eliminating non-relevant attributes) and editing (reduction of the number of examples by eliminating some of them or calculating proto types). Our algorithm belongs to the first group. Feature selection methods can be grouped into two categories from the point of view a method’s output. One category is about ranking feature according to same evaluation criterion; the other is about choosing a minimum set of features that satisfies an evaluation criterion.

In this work we are using Discriminative optimal criterion (DOC), DoC is pragmatically advantageous because it attempts to directly maximize the classification accuracy and naturally reflects the Bayes error in the objective. To make DoC computationally tractable for practical tasks, we propose an algorithmic framework, which selects a subset of features by minimizing the Bayes error rate estimated by a nonparametric estimator. A set of existing algorithms as well as new ones can be derived naturally from this framework. As an example, we show that the Relief algorithm greedily attempts to minimize the Bayes error estimated by the k-Nearest Neighbor (kNN) method. This new interpretation insightfully reveals the secret behind the family of margin-based feature selection algorithms and also offers a principled way to establish new alternatives for performance improvement. In particular, by exploiting the proposed framework, we establish the Parzen-Relief (P-Relief) algorithm based on Parzen window estimator, and the MAP-Relief (M-Relief) which integrates label distribution into the max-margin objective to effectively handle imbalanced and multiclass data.

Feature selection is an important issue in pattern recognition and machine learning which helps us to focus the attention of a classification algorithm on those features that are the most relevant to predict the class. Theoretically, if the full statistical distribution were known, using more features could improve results. However, in practical a large number of features as the input of induction algorithms may turn them inefficient as memory and time consumers. Besides, irrelevant features may confuse algorithms leading to reach false conclusions, and hence producing even worse results. So it is of fundamental importance to select the relevant and necessary features in the preprocessing step. Obviously, the advantages of using feature selection may be improving understandability and lowering cost of data acquisition and handling. Because of all these advantages, feature selection has attracted much attention within the Machine Learning, Artificial Intelligent and Data Mining communities. As a part of any feature selection method, there are several factors that need to be considered, the most important are: the estimation measure and the search strategy.

Typical estimation measures can be divided into: filters and wrappers. Filter based feature selection methods are in general faster than wrapper based methods. As one of the filter based feature selection methods, the RELIEF algorithm is an effective, simple, and widely used approach to feature weight estimation. The weight for a feature of a measurement vector is defined in terms of feature relevance. In , a probabilistic interpretation of RELIEF is made, which states that the learned weight for a feature is propositional to the difference between two conditional probabilities. These two probabilities are of the value of a feature being different conditioned on the given nearest miss and nearest hit, respectively. Thus, RELIEF usually performs better than the other filter based approaches due to the feedback of the nearest-neighbor classifier;

In addition, RELIEF is often more efficient than the wrapper approach because RELIEF determines the feature weights through solving a convex optimization problem. However, the RELIEF algorithm has a relatively distinct defect that the feature weight may fluctuate with the instances. And in the majority of cases, the instances acquired are at random. Moreover, according to the RELIEF algorithm, the frequency in sampling is also with uncertainty. Therefore, RELIEF algorithm is unstable and reduces the accuracy of expected results. In this paper, a novel reliefF feature selection algorithm based on Mean-Variance model is proposed. Both the mean and the variance of the samples discrimination are considered as the criterion of feature weight estimation. In this way, the results are more stable and accurate. Finally, the experiments of the real seismic signals of ground targets are operated whose results indicate that the subsets of feature generated by proposed algorithm have better performance..

RELEIF-F ALGORITHM

Proposed algorithm structure

The original relief can deal with nominal and numerical attributes. However, it cannot deal with incomplete data and is limited to two-class problems. Its extension, solve these and other problems, is called ReliefF. The ReliefF (Relief-F) algorithm is not limited to two class problems, is more robust and can deal with incomplete and noisy data. Similarly to Relief, ReliefF randomly selects an instance Ri (line 3), but then searches for k of its nearest neighbors from the same class, called nearest hits Hj (line 4), and also k nearest neighbors from each of the different classes, called nearest misses Mj(C) (lines 5 and 6). It updates the quality estimation W[A] for all attributes A depending on their values for Ri, hits Hj and misses Mj(C) (lines 7, 8 and 9). The update formula is similar to that of Relief (lines 5 and 6 on Figure 1), except that we average the contribution of all the hits and all the misses. The contribution for each class of the misses is weighted with the prior probability of that class P(C) (estimated from the training set). Since we want the contributions of hits and misses in each step to be in [0;1] and also symmetric (we explain reasons for that below) we have to ensure that misses’ probability weights sum to 1. As the class of hits is missing in the sum we have to divide each probability weight with factor 1¡P(class(Ri)) (which represents the sum of probabilities for the misses’ classes). The process is repeated for m times. Selection of k hits and misses is the basic difference to Relief and ensures greater robustness of the algorithm concerning noise. User defined parameter k controls the locality of the estimates. For most purposes it can be safely set to 10. To deal with incomplete data we change the diff function. Missing values of attributes are treated probabilistically.

Algorithm representation

 The Input :for each training instance a vector of attribute values and the class value

 Output : the vector w of estimations of the qualities of attributes.

1.set all weights w[A]:=0.0;

2.for i:=1 to m do begin

3.randomly select an instance ;

4.find k-nearest hits

5.for each class C class() do

6.from class C find k nearest misses (c);

7.for A:=1 to a

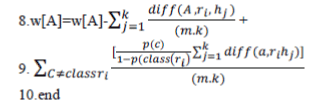Bayes Error Estimation

The Bayesian estimation is a framework for the formulation of statistical inference problems. In the prediction or estimation of a random process from a related observation signal, the Bayesian philosophy is based on combining the evidence contained in the signal with prior knowledge of the probability distribution of the process. Bayesian methodology includes the classical estimators such as maximum a posteriori (MAP), maximum-likelihood (ML), minimum mean square error (MMSE) and minimum mean absolute value of error (MAVE) as special cases. The hidden Markov model, widely used in statistical signal processing, is an example of a Bayesian model. Bayesian inference is based on minimization of the so-called Bayes’ risk function, which includes a posterior model of the unknown parameters given the observation and a cost-of-error function. Introduction to the basic concepts of estimation theory, and considers the statistical measures that are used to quantify the performance of an estimator. We study Bayesian estimation methods and consider the effect of using a prior model on the mean and the variance of an estimate. The estimate–maximize (EM) method for the estimation of a set of unknown parameters from an incomplete observation is studied, and applied to the mixture Gaussian modeling of the space of a continuous random variable. This chapter concludes with an introduction to the Bayesian classification of discrete or finite-state signals, and the K-means clustering method.

Bayesian theory is a general inference framework. In the estimation or prediction of the state of a process, the Bayesian method employs both the evidence contained in the observation signal and the accumulated prior probability of the process. Consider the estimation of the value of a random parameter vector θ, given a related observation vector y. From Bayes’ rule the posterior probability density function (pdf) of the parameter vector θ given y, fΘ |Y (θ | y) , can be expressed as

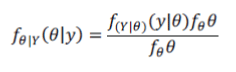Where for a given observation, fY(y) is a constant and has only a normalizing effect. Thus there are two variable terms in Equation (4.1): one term fY|Θ(y|θ) is the likelihood that the observation signal y was generated by the parameter vector θ and the second term is the prior probability of the parameter vector having a value of θ. The relative influence of the likelihood pdf fY|Θ(y|θ) and the prior pdf fΘ(θ) on the posterior pdf fΘ|Y(θ|y) depends on the shape of these function, i.e. on how relatively peaked each pdf is. In general the more peaked a probability density function, the more it will influence the outcome of the estimation process. Conversely, a uniform pdf will have no influence. where the terms in the exponential function have been rearranged to emphasize the illustration of the likelihood space in Figure 1.

RESULTS AND DISCUSSIONS

Here we open our project into net beans IDE, and run our project, then we get one new window with some buttons and console space. And this window contains buttons like browse, built Data set, Normalize, select measures, ReliefF+knn, Parzen+ReliefF, execute, do cluster, and report. In this Browse button is used for to take input for the algorithm, and next we built our project and next we perform normalization operation on our data set for better outputs because normally data set having some missing values, un relevant values and multi class problems so we need to perform this normalization. And next we select type of measurement we want to perform on the data set for assuming the near hit and near miss. Next we select the algorithm, which we want to perform on the data set. After that execute button, and do cluster buttons. Next we get the total project results we are having the report button. 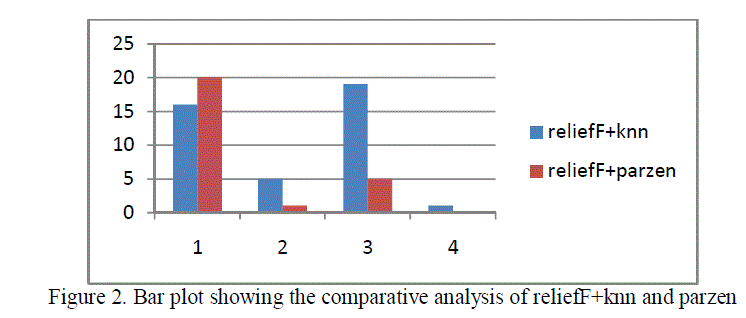Finally it generates the report about output as shown in the Fig.2 through 4. The graph shows, discrimination between reliefF+knn and parzen+relief. In this we are showing the no of features selected by using two algorithms with respect to similarity threshold value.

CONCLUSION

In this work,we are comparing the two feature weighting algorithms. So the selected relevant features are showing in clusters by using some clustering algorithms for better validation. limitations of the well known clustering techniques for large data sets and the details of the proposed clustering method, Leaders–Subleaders, have been presented. Our experimental results on numerical data sets show that the Leaders–Subleaders algorithm performs well. Hierarchical structure with required number of levels can be generated by the proposed method to find the subgroups/subclusters within each cluster at low computation cost. The representatives of the subclusters help in improving the CA (classification accuracy). Davies-Bouldin index showed a good performance to the results were equivalent, even with the different radius.

Figures at a glance

Figure 1

References

G. Carneiro and N. Vasconcelos, “Minimum Bayes Error Features for Visual Recognition by Sequential Feature Selection and Extraction,” Proc. Computer and Robot Vision Conf. (CRV ’05), pp. 253-260, 2005 M.A. Hall and G. Holmes, “Benchmarking Attribute Selection Techniques for Discrete Class Data Mining,” IEEE Trans. Knowledge and Data Eng., vol. 15, no. 6, pp. 1437-1447, Nov./Dec. 2003. E. Choi and C. Lee, “Feature Extraction Based on the Bhattacharyya Distance,” Pattern Recognition, vol. 36, no. 8, pp. 1703-1709, 2003. M. Dash and H. Liu, “Feature Selection for Classification,” Intelligent Data Analysis, vol. 1, nos. 1-4, pp. 131-156, 1997. K. Fukunaga and D.M. Hummels, “Bayes Error Estimation Using Parzen and k-NN Procedures,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. PAMI-9, no. 5, pp. 634-643, Sept. 1987. R. Gilad-Bachrach, A. Navot, and N. Tishby, “Margin Based Feature Selection—Theory and Algorithms,” Proc. 21st Int’l Conf. Machine Learning (ICML ’04), 2004. I. Guyon and A. Elisseeff, “An Introduction to Variable and Feature Selection,” J. Machine Learning Research, vol. 3, pp. 1157- 1182, 2003.