Comparative Analysis of Fragment based and
Exemplar based Inpainting Techniques

J. N. Kazi; Y.M. Patil

Comparative Analysis of Fragment based and Exemplar based Inpainting Techniques

J. N. Kazi¹ , Y.M. Patil²

Lecturer, Dept. of Electronics & Telecommunication, Shivaji University, Kolhapur, Maharashtra, India¹
Assistant Professor, Dept. of Electronics & Telecommunication, Shivaji University, Kolhapur, India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Inpainting is an art of modifying the digital image in such a way that the modifications/alterations are undetectable to an observer who is unknown of the original image. Applications of this technique include restoration of damaged photographs & films, removal of superimposed text, removal/replacement of unwanted objects. After the user selects a region to be inpainted the algorithm automatically fills in these holes by data sampled from remainder of the image. In past the problem of inpainting was addressed by two classes of algorithms (i) “diffusion based inpainting” and (ii) “texture synthesis”. Further extensive research has undergone in this field which resulted in variety of inpainting techniques. In this paper we will compare Fragment based [2] and Exemplar based [1] inpainting techniques.

Keywords

Exemplar, Inpainting, Texture synthesis, Object removal, Fragment.

INTRODUCTION

In real world so many times it is needed to have a system to recover the damaged photographs, artwork design, drawing etc. That means removal of portions of an image is an important tool in photo editing and film post-production. The unknown regions can be filled in by various interactive procedures such as clone brush strokes, and compositing processes. Such interactive tools require meticulous work driven by a professional skilled artist to complete the image seamlessly. This process is time consuming and leads manual errors in reconstruction. the problem of image completion was addressed by two sets of algorithms which are (i) inpainting [Bertalmio et al. 2000 [5]]- which works well in reconstructing linear structures such as small scratches, and (ii) texture synthesis [Efros and Leung 1999 in [7]]; Wei and Levoy 2000 [6]; Efros and Freeman 2001 [4]] which works well for repetitive two dimensional textures. The objective of image inpainting technique is to reconstruct both structure and texture of damaged image in a visually plausible manner.

In this paper we will compare “Fragment based” and “ Exemplar based” inpainting techniques in terms of efficiency, accuracy and time consumption.

EXEMPLAR BASED REGION FILLING ALGORITHM

The proposed algorithm uses isophote driven image sampling process. The algorithm takes the known image patches i.e. exemplars and propagates them into the missing regions. To handle the missing region with composite textures and structures, patch priority is defined to encourage the filling order of patches on the structure.

First, given an input image I, the user selects a target region Ω to be removed and filled. The source region Φ is defined as the entire image minus target region (I- Ω) see fig 1. The source region provides samples used in the filling process. The contour of the target region is denoted by δΩ which is also referred as “fill front”. The size of template window Ψ must be specified. A default window size is 9 x 9 pixels but in practice require the user to set it to be slightly larger than the largest “texel” in the source region

Once these parameters are determined the algorithm proceeds automatically. The heart of this algorithm is priority/ patch ordering mechanism that allows exemplar based approach to handle the structural features of an input image. Priority is composed of two terms- Confidence term denoted by C(P) and the data term D(P)both are defined over pixels.

ÃÂ¯ÃâÃÂ· C(p) = ( Sum{q \in Ψp \intersect (I-Ω)}C(q) ) / ( area of patch )

ÃÂ¯ÃâÃÂ· D(p) = abs( Isophote(p). Normal(p) ) /alpha

Confidence term is a measure of reliable information surrounding the pixel P. Confidence tends to decay as the centre of the fill region is approached. Confidence is used to capture the texture property but it ignores structural information in the image because of which if priority only consisted the confidence term, the patches would be selected in an “onion peel” manner which may lead to visible artefacts such as unrealistically broken structures.

The data term D(P) is the function of how strong an isophote hits the boundary/contour δΩ at each iteration, it captures the "strength of flow" of an edge. It encourages the linear structures to be synthesized first and therefore propagated securely into the target region. The proposed algorithm computes the priority by considering both confidence term C(P) and data term D(P) in order to get good results in images containing both texture and structure information. The algorithm iterates the following three steps until all pixels have been filled.

A Computation of patch priorities:

The strategy of the proposed algorithm is to perform synthesis task through a best first filling that depends upon the priorities assigned to each patch on the fill front. Patches those are on the continuation of strong edges and those which are surrounded by high confidence values play an important role in priority computation.

Considering a patch Ψp centered at point P for some P ÃÂÃâ δΩ as shown in fig.1, the priority P(P)is defined as the product of two terms

P(_P)=C(_P)D(_P)

The confidence term C(_P) and the data term D(_P) are defined as follows:

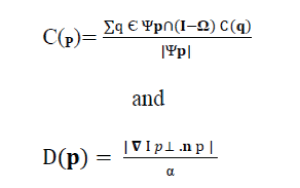Where |Ψp| is the area of the patch,α is the normalization factor (e.g. α=255 for a typical gray level),n p is a unit vector orthogonal to front δΩ in the point P and ÃÂ¢ÃâÃÂ´ denotes the orthogonal operator. The priority P(P) is computed for every border patch , with a distinct patches for each pixel on the boundary of the target region. During initialization the function C(P) is set to C(P)=0 for all pixels belonging to target region Ω and C(P)=1 for all pixels belonging to source region (I- Ω)i.e. Φ.

B Propagating Texture and Structure information:

Once all the priorities on the fill front are computed, the target patch ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ with highest priority is found and then it is filled with data sampled from the source region Φ. The algorithm propagates image texture by direct sampling of the source region. Then the patch from the source region which is most similar to the target patch ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ is searched, which is defined as follows:

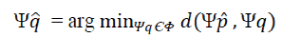Where the distance d(Ψ a, Ψb) between two generic patches Ψ a and Ψb is simply defined as the sum of squared differences (SSD) of the already filled pixels in two patches. pixel colors are represented in CIE Lab color space.

After finding the exemplar patch ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ , the value of each pixel to be filled is p′ | p′ ÃÂÃâ ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ ∩ Ω is copied from its corresponding position inside ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ this achieves the propagation of both structure and texture information from the source region Φ to the target region Ω, one patch at a time.

C Updating Confidence values:

After the target patch ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ is filled with new pixel values, the confidence C(P) is updated in the area occupied by ΨÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ as follows:

Above equation allows to measure the relative confidence of patches on the fill front, without image specific parameters. As filling proceeds, confidence values decay, indicating that the color values of pixels near the centre of the target region are less sure.

D Pseudo code description of region filling algorithm:

Extract manually selected initial front δΩ°

Repeat following steps until the region is completely filled

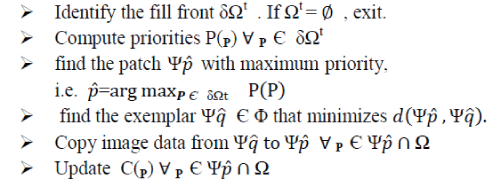E. Implementation details:

Now let us focus on a single iteration of this algorithm to show how structure and texture are adequately handled by exemplar based synthesis. Suppose that the square template ΨP ÃÂÃâΩ .centred at the point P [Fig.2 (b)] is to be filled. The best-match sample from the source region comes from the patch Ψq ÃÂÃâ Ω. , which is most similar to those parts that are already filled in Ψp. In the example in Fig. 2(b), we see that if Ψp lies on the continuation of an image edge, the most likely best matches will lie along the same (or a similarly colored) edge [e.g., Ψq’ and Ψq’’ in Fig. 2(c)]. All that is required to propagate the isophote inwards is a simple transfer of the pattern from the best-match source patch [Fig. 2(d)].

FRAGMENT BASED IMAGE INPAINTING

Given an image and an inverse matte the goal of algorithm is to complete the unknown regions based on the known regions.

We assume that foreground elements or background regions are roughly marked with an image editing tool, or a more accurate α channel is extracted using a matting tool. This defines an inverse matte α¯ that partitions the image into three regions: the known region,

where α¯ i =1; unknown region, where α¯ i =0; and, optionally, a gray region, where 0 <α¯ i < 1 for each pixel i, and “inverts” the common definition of trimaps that are generated in the process of pulling a matte and foreground elements from an image [Chuang et al. 2002]. We require a conservative inverse matte that, at least, contains the entire extracted region. As in digital image matting, the regions of the inverse matte are not necessarily connected. The inverse matte defines a confidence value for each pixel. Initially, the confidence in the unknown area is low. However, the confidence of the pixels in the vicinity of the known region is higher. The confidence values increase as the completion process progresses.

The approach to image completion follows the principles of figural simplicity and figural familiarity. Thus, an approximation is generated by applying a simple smoothing process in the low confidence areas. The approximation is a rough classification of the pixels to some underlying structure that agrees with the parts of the image for which we have high confidence. Then the approximated region is augmented with familiar details taken by example from a region with higher confidence.

All of these processes are realized at the image fragment level. A fragment is defined in a circular neighborhood around a pixel. The size of the neighbourhood is defined adaptively, reflecting the scale of the underlying structure. Image completion proceeds in a multiscale fashion from coarse to fine, where first, a low resolution image is generated and then the results serve as a coarse approximation to the finer level For every scale neighbourhoods are considered in level sets from high to low confidence. Figure 3 shows the confidence and colour values at different time steps in each scale.

At each step, a target fragment is completed by adding more detail to it from a source fragment with higher confidence. Typically, the target fragment consists of pixels with both low and high confidence. The pixel values which are based on the approximation generally have low confidence, while the rest of the fragment has higher confidence. For each target fragment the algorithm searches for a suitable matching source fragment, to form a coherent region with parts of the image which already have high confidence. The search is performed under combinations of spatial transformations to extend the training set and make use of the symmetries inherent in images. The source and target fragments are composited into the image. The algorithm updates the approximation after each fragment composition. As fragments are added, the mean confidence of the image converges to one, completing the image. A high-level description of this approach appears in Figure 4. In the pseudo code, the following terms are emphasized: (i) approximation, (ii) confidence map, (iii) level set, (iv) adaptive neighbourhood,(v) search, and (vi) composite. These are the building blocks of our technique. In the following sections we elaborate on each in detail.

A Pseudocode Representation

Input: image C, inverse matte α¯ (∃ pixel with α¯ < 1)

Output: completed image, α¯ = 1

Algorithm:

ÃÂ¯ÃÆÃË for each scale from coarse to fine approximate image from color and coarser scale

ÃÂ¯ÃÆÃË compute confidence map from α¯ and coarser scale

ÃÂ¯ÃÆÃË compute level set from confidence map

ÃÂ¯ÃÆÃË while mean confidence < 1−ÃÂ¢ÃâÃÂ» ÃÂ¢ÃâÃÂ» for next target position p

ÃÂ¯ÃÆÃË compute adaptive neighborhood N(p)

ÃÂ¯ÃÆÃË search for most similar and frequent source match N(q)

ÃÂ¯ÃÆÃË composite N(p) and N(q) at p,

ÃÂ¯ÃÆÃË updating color and α¯ compute

ÃÂ¯ÃÆÃË approximation, confidence map and update level set

Comparison between “Fragment based” and “Exemplar based” inpainting

In this section we will compare “Fragment based” and “Exemplar based” image inpainting techniques, results of the two techniques are compared in terms of their efficiency and time taken for inpainting.

As it can be seen that both techniques work noticeably well in object removal but Fragment based inpainting technique tends to introduce some edge blur see Fig 4(b) where as Exemplar based inpainting has resulted in blur free output image, also the time taken for inpainting by Exemplar based method is less compared to Fragment based method.

CONCLUSION

The paper compares “fragment based” and “Exemplar based ” inpainting techniques in terms of their efficiency and time taken for inpainting. The former attempts to synthesis missing regions from coarse to fine levels by assigning fragments (i.e. circular regions) with higher Confidence; and the later searches for most similar patches (Exemplars) to fill the target region. It is found that both techniques work noticeably well in removal of object from still images ; but fragment based method introduces little blur while inpainting the edge where as “Exemplar based” inpainting technique produces blur free output and also takes less time for inpainting as compared to Fragment based method..

FUTURE SCOPE

Further work can be done in order to improve the speed efficiency of the inpainting techniques also the work can be extended to the object removal form videos.

Tables at a glance

Table 1

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

References

A. Criminisi, P. Perez and K. Toyama. “Region filling and Object Removal by Exemplar-based image Inpainting”, IEEE trans. On Image Processing, Vol. 13, No. 9, Sept 2004
I. Drori, D. Cohen-Or, and H. Yeshurun, “Fragment-based image completion,”in ACM Trans. Graphics (SIGGRAPH),vol. 22, San Diego,CA, 2003, pp. 303–312.
Chuang, Y.-Y., Agarwala, A., Curless, B., Salesin, D. H., AND Szeliski, R. 2002. Video matting of complex scenes. ACM Transactions on Graphics, 21, 3, 243– 248.
A. Efros and W. T. Freeman, “Image quilting for texture synthesis and transfer,” in Proc ACM Conf. Computer Graphics (SIGGRAPH), Aug. 2001, pp. 341–346.
M. Bertalmio, G. Sapiro, V. Caselles, and C. Ballester, “Image inpainting,” in Proc. ACM Conf. Comp. Graphics SIGGRAPH), New Orleans, LA, July 2000, http://mountains.ece.umn.edu/guille/inpainting htm, pp. 417–424.
L.-W. Wey and M. Levoy, “Fast texture synthesis using tree-structured vector quantization,” in Proc. ACM Conf. Computer Graphics (SIGGRAPH), 2000.
A. Efros and T. Leung, “Texture synthesis by nonparametric sampling,” in Proc. Int. Conf. Computer Vision, Kerkyra, Greece, Sept. 1999, pp. 1033–1038.