International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparative Analysis of Methods to Denoise CT Scan Images

Tarandeep Chhabra 1, Geetika Dua2, Tripti Malhotra3
  1. Student, Dept. of ECE, Doon Valley Institute of Engineering & Technology, Karnal, India 1
  2. Student, Dept. of ECE, IIT, Ropar, India 2
  3. Assistant Professor, Dept. of ECE, Doon Valley Institute of Engineering & Technology, Karnal, India3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Medical images are generally noisy due to the physical mechanisms of the acquisition process. In CT Scan there is a scope to adapt patient image quality and dose. Reduction in radiation dose (i.e the amount of X-rays) affects the quality of image and is responsible for image noise in CT. Most of the denoising algorithms assume additive white Gaussian noise but however most medical images may contain non Gaussian noise like poisson noise in CT. This paper contains the comparative analysis of a number of denoising algorithms namely wiener filtering, wavelet decomposition, anisotropic diffusion, anisotropic diffusion in wavelet domain, wave atom decomposition, median filtering and NL-means filtering. Then, some quantitative performance metrics like PSNR, SNR, MSE, S/MSE and MAD are computed. This comparison helps in the assessment of image quality and fidelity. We conclude that the anisotropic diffusion in wavelet domain is the most efficient method in removing poisson noise from CT Scan images.

Keywords
Computed, tomography, noise, reduction, filtering, wavelet, anisotropic, SNR, MSE.

INTRODUCTION
Ct scan stands for computed tomography. It basically uses x-rays to obtain structural and functional information about the human body. In ct, the image quality is influenced by many technical parameters. One of the most important parameter is the radiation dose. The quality of image increases with the significant amount of radiation dose [1]. But an increased amount of x-rays being absorbed by the human body increases the chances of cancer. So we need to reduce the radiation dose which is responsible for image noise in ct. So for proper analysis and diagnosis, it is required to reduce the image noise. Noise removal therefore plays a vital role in medical imaging applications in order to enhance and recover the analysis details that may be hidden in the data. For this purpose filtering is thus applied to clear such images. Any noise reduction algorithm aims to enhance the fidelity of an image which actually means removing the random and uncorrelated structures and retaining the resolution. Denoising of image data has been an active area of research and different methods such as median filtering, wiener filtering, use of nlm filter, wavelets decomposition, wave atom, bilateral filtering, isotropic, anisotropic diffusion, etc have been used.

METHODS TO REDUCE NOISE IN CT SCAN IMAGES

A. Median Filter
Linear filters are generally used to reduce noise in CT images. Here, the neighboring pixels represent the additional samples of the same value as that of reference pixel. In linear filters the convolution process is used for implementing the neighboring kernels as neighborhood function. But this may lead to the blurring of edges. To overcome such a problem non-linear filters are used for noise reduction. These filters help to preserve edges. Median filter is an example of non-linear filters. In median filter, the ranking of the neighboring pixels is done according to the intensity or brightness level and value of the pixel under evaluation is replaced by the median value of surrounding pixel values.
image
Neighborhood values:
115,119,120,123,124,125,126,127,150
Median value= 124
Median filter can therefore effectively denoise medical images. The images distorted or blurred by shot or impulse noise can excellently denoised using this filter. Median filters have many advantages over smoothening filters [9]:
 In median filter the output values consist of only those present in the neighborhood (median value) so there is no reduction in contrast across the steps.
 The boundaries are also not shifted when median filter is used.
 The edges are minimum degraded and hence median filter can be repeatedly applied.

B. Wavelet Decomposition
The term Wavelet means a short wave like oscillation. Its amplitude value starts from zero, increases, again degrades to give zero value.
Wavelet transform is actually a mathematical technique which is used to synthesize a signal in time domain. It can be combined with any unknown signal to analyze that signal [8]. Then the transform of each segment is computed. At high frequencies this transform gives poor frequency but good time resolution, and vice-versa.
In wavelet transform the analysis of data variables is done in both time and frequency domain. In DWT a signal is represented in terms of displacement functions φ and scale functions ψ.
In DWT the signal can be decomposed into several levels and then these levels are analyzed independently. Signal decomposition (using orthogonal wavelets) can be shown by the equation:
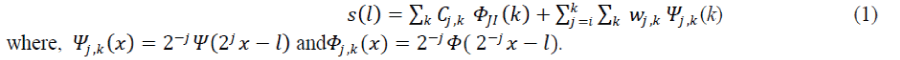image
Threshold is applied to the wavelet coefficients for noise reduction. Threshold is further of two types:
(i) Soft threshold
(ii) Hard threshold
Soft and hard threshold can be given as:
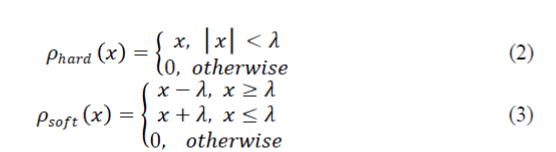image
Further, there are a number of basis functions that can be used as mother wavelet for wavelet transformation. Commonly used wavelet functions are haar, daubechies, coiflet, symmlet ,etc. the wavelets are chosen based on their shape and their ability to analyse the signal in a particular application.

C. Wave atom Transform
Wave atoms are used for harmonic computational analysis. These are a variant of 2D wavelet packets that retains an isotropic aspect ratio [6]. They have a sharp frequency localization that cannot be achieved using a filter bank based on wavelet packets. Wave atoms obey the parabolic scaling law : wavelength ͂ (diameter)2. The name “wave atom” comes from the property that they provide an optimally spars representation of wave propagator with applications to fast numerical solvers for wave equation.

D. Wiener Filter
Wiener filters are basically the optimum linear filters which involves linear estimation of a desired signal sequence from another related sequence while solving the linear filtering problem certain important parameters like mean and correlation functions of useful signal and unwanted additive noise are assumed. Now the aim is to design a linear filter whose input is the noisy data and output is required to minimize the effect of noise[10]. The filter optimization problem is to minimize the value of MSE that is defined as mean square value of error. It is the difference between the desired and the actual filter output. The resulting solution (for stationary inputs)is called the wiener filter. However, wiener filter is inadequate for non stationary inputs because in such a case the optimum filter has to assume a time varying form. In wiener filter, the performance function is given as:
image
This is called “mean square error criterion”

E. Anisotropic Diffusion
Diffusion filtering of an image is similar to the physical diffusion process which provides equilibrium while following the law of conservation of mass. The image intensity can be seen as „concentration‟. The noise can be seen as noise inhomogenities. The inhomogenities can be smoothened by „diffusion‟. Diffusion filtering is digital image processing is mainly of two types: linear and non linear. Since the diffusion process relates a concentration gradient with a flux, linear isotropic diffusion is that in which these quantities are parallel [2]. Linear isotropic diffusion is used for image smoothening. The main disadvantage is that it blur the important features like edges. In nonlinear diffusion the concentration gradient and flux are not parallel and the filter coefficients change in response to differential structures within the image[3].
The first inhomogeneous diffusion model (anisotropic diffusion) was given by Perona and Malik [7]. Their idea was to vary the noise removal in nearly homogeneous regions while avoiding any alteration of the signal along significant discontinuities. The discontinuities are edges in images that arise due to the sharp changes in image intensity. The change in intensity I over time was defined as[7]:
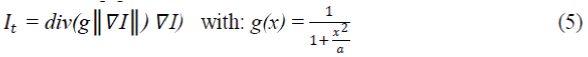image
where g is the conduction function.

F. Anisotropic Diffusion in Wavelet Domain
Various wavelet shrinkage algorithms denoise image by reduce wavelet coefficient. These algorithms using statistical properties of wavelet coefficients, but seldom use the neighbor or local information. On other hand, image anisotropic diffusion using neighbor information and adjust diffusion conductivity by edge magnitude, but can‟t distinguish edges produced by noise and image structures. It is naturally that we expect by combines these two techniques produced better result than either.
Anisotropic diffusion was performed in stationary wavelet domain. The overall framework of proposed denoising is shown in the figure below:
„I‟ is input noisy image, „SWT‟ and „ISWT‟ means stationary wavelet transform and inverse stationary wavelet transform, „D‟ and „A‟ means detail and approximate wavelet coefficients, including multi-scale coefficients. „D'‟ is denoised wavelet coefficients after anisotropic diffusion. At last, „ I ' ‟ is final denoised image.

G. NLM Filter
The aim of any denoising method is to recover the original image from a noisy environment,
v(i) = u(i) + n(i)
where v(i) is the observed value, u(i) is the actual or the true value and n(i) is the noise perturbation at a pixel i. Several methods can be used to denoise and recover the true image u. One such method is to use NLM (non- local means) filter[4]. The NL- means algorithm is defined by the formula:
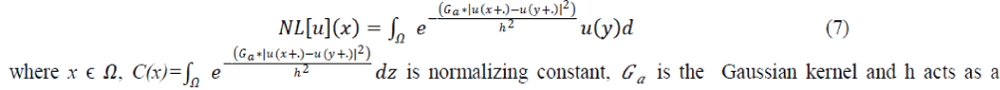`image
filtering parameter.
According to this formula the denoised value at x is the mean of all the values at all the points whose Gaussian neighborhood is as the neighborhood of x.

COMPARISON PARAMETERS
The final step is to compute comparison parameters to compare the results of all above described techniques.

A. Mean Square Error (MSE)
Mean square error is a dominant quantitative performance metric in the field of image processing. It is used for the assessment of image quality and fidelity. The cumulative squared error that occurs between compressed and original form of image is termed as MSE. It is mathematically defined as:
image
where m is the number of rows in the image, N(i,j) is noisy image and DN(i,j) is denoised image.

B. Peak Signal To Noise Ratio
PSNR is mathematically described as:
image
where R is the maximum fluctuation in the input image data type. For example, if the input image has a double precision data type, R=1[6]. The PSNR value approaches infinity as the MSE approaches zero. Higher value of PSNR represents higher image quality. Small value of PSNR represents high numerical differences between images.

C. Signal To Noise Ratio
The signal-to-noise ratio is a technical term used to characterize the quality of the signal detection of a measuring system. It is mathematically described as:
image
where x is the noise free simulated images and �� is noisy or denoised image.

D. Signal To Mean Square Error
Signal to mean square error is the ratio of signal power to mean square error where mathematical representation of MSE is given in equation (8).

E. Mean Absolute Difference
Mean is the average calculated by adding up some numbers and dividing by how many they are. Absolute is the number in which we don‟t bother to look at the positives or negatives. We just assume them as positives.
„Mean absolute difference‟ is a common measure of how much a set of observations differs from the average (without bothering whether it is above or below average).

RESULTS AND DISSCUSSION
This paper contains the results, obtained after following the wiener filtering, wavelet decomposition, anisotropic diffusion, anisotropic diffusion in wavelet domain, wave atom decomposition, median filtering and NL-means filtering. Further, comparison parameters like PSNR, MSE, SNR, S/MSE and MAD are computed and compared.

CONCLUSIONS
In this paper, we demosntrated the image denoising results obtained from various denoising alorithms namely median filtering, wavelet decomposition, anisotropic diffusion, anisotropic diffusion,in wavelet domain, waveatom decomposition, weiner filtering and NL-m filtering. By investigating the comparison parameters, it is clear that anisotropic diffusion technique in wavelet domain is promising. This method smoothes the noise while preserving the important features like edges. It includes the benefits of both the techniques namely anisotropic diffusion and wavelet decomposition. This techniques provides the maximum PSNR, SNR, S/MSE and minimum MSE and MAD. So, from the comparative analysis of all the above described denoising algorithms it is clear that anisotropic diffusion method when used in wavelet domain is best among all discussed above.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 4 Figure 5 Figure 6
Figure 4 Figure 5 Figure 6
 

References
  1. Micheal F. McNitt-gray, “Tradeoffs in CT Image Quality and Dose”, the C.V. Mosby company,london.
  2. Adrienne M. Mendrik, “Noise Reduction in Computed Tomography Scans Using 3-D Anisotropic Hybrid Diffusion with Continuous switch”, IEEE Transactions on medical imaging, VOL.28, pp.10, OCTOBER 2009.
  3. S.K. Weeratunga, “A comparison of PDE-based non-linear anisotropic diffusion techniques for image denoising”, SPIE Electronic Imaging, Santa Clara,january 2003.
  4. Antony Buades, “A non-local algorithm for image denoising”.
  5. Alian Hore, “Image quality metrics: psnr vs ssim”,2010 international conference on pattern recognition.
  6. Geetika Dua, “Denoising MRI images using Wavw Atom Transform”, International Conference on sports biomechanics, Emerging Technologies and Quality Assurance in Technical Education,2012.
  7. Mathieu Desbrun, “anisotropic feature preserving denoising of height fields and bivariate data.
  8. http://users.rowan.edu/~polikar/WAVELETS/WTpart3.html
  9. Sin HOONG Teoh, “exploreation of current trend on median filtering methods utilized in digital grayscale image processing”, IJMMM 2013 VOL1(1):50-54 ISSN:1793-8198.
  10. Suresh Kumar, “Performance comparison median and wiener filter in image denoising”, IJCA Journal Number 4,article 7, year of publication 2010.
  11. Kazubek, “Wavelet domain image denoising by thresholding and wiener filtering”, IEEE Volume-10,Issue 11, Nov 2003 265 Vol.3.