Comparative Response Analysis through
Optimized Transfer Function Generation for
Two Standard Dexterous Arm Model

Swati Barui; Payel Biswas; Santu Gharai

Comparative Response Analysis through Optimized Transfer Function Generation for Two Standard Dexterous Arm Model

Swati Barui ¹, Payel Biswas², Santu Gharai³

Asst. Prof, Dept. of ECE, Narula Institute of Technology, Kolkata, India ¹
Asst. Prof, Dept. of ECE, Narula Institute of Technology, Kolkata, India ²
M Tech Scholar, Dept. of ECE, Narula Institute of Technology, Kolkata, India ³

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The recent developments of dexterous arm are remodeled with different implementations of biomedical control engineering. Realization of artificial limb to restore the originality of concerned for overall function of the living system is the science popularly known as prosthetic and dexterity is the ease of hand movement.A prosthetic limb needs to be well connected to the original connecting organ for faithful function of overall system. Hence, the limb should be capable of processing various intelligences as obtainable from the total living system. Researches are going on for the improvement of stability of some existing standard prosthetic arm model. In this study, an approach is taken to establish the gain of two reference transfer functions through Hurzwitz matrix construction for comparative result analysis.

Keywords

Dexterity,Control model,Hurzwitz matrix,Comparative Analogy.

INTRODUCTION

Dexterity, adroitness in using the hands or body, is the prime or essential aspect in modelling dexterous hand. A prosthesis ,prosthetic, or prosthetic limb is an artificial device extension that replaces a missing body part [1]. One of the advanced concept of designing of prosthetic arm is proposed by the concept of a virtual prosthetic control system of prosthetic arm presented by the analysis of a grasp motion. The concept of the artificially generated limb connected to the nervous system to be in immediate contact to the concerned limb and lastly to brain system able to make the overall control of the total living system was introduced in the new prospective [3]. In the present work two transfer functions corresponds to two standard dexterous models are taken to get the optimum gain by constructing the Hurzwitz matrix.Then a comparative study with step response analysis is done to achieve the better model.

LITERATURE SURVEY

The first practical prosthesis system was demonstrated in Hanover, Germany-the developments were slow. Increasing use of prosthetic control started in North America in the late 1970s, in children in Sweden since 1976 and in the United Kingdom since 1978. Now a day it is felt that construction of the prosthesis is a satisfactory solution in providing the patient with as much light hand and arm mobility as possible for providing proper dexterity [2]. In 21st century the design and construction to the Hand prosthesis has shown great progress. Among this kind of prosthesis some are commercially available like well-known Otto Bock Sensor Hand, the Utah Arm and the I-Limb Hand from touch bionics are among the others [3].

A typical close-loop system block diagram of prosthetic arm with body interfacing is shown in fig.1. The entire system is composed of subsystems based on the simple feedback control system.The desired position and the sensed position generates an error signal to the nervous system. The electromyography (EMG) signal impulses are picked up by special sensor and an amplifier produces a voltage to drive the motor. The output of the motor circuit is the velocity of the limbs in one dimension that incorporates the limb position [4,7].

CONTROL MODEL ANALYSIS

Control model analysis is constructed for two reference cases and block diagram representation and standard transfer functions are shown below:

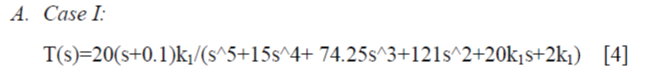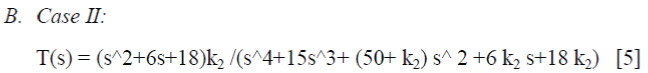The two standard transfer functions are represented in block diagram form as shown in fig. 2 and fig. 3.

APPROACH TO FIND THE VALUE OF GAIN

A. General Flow Chart

The flowchart to find out the Gain of the above transfer functions through Hurwitz matrix formation is shown below .It describes the steps successively to get the Gain of the concerned transfer functions.

In mathematics, a Hurwitz matrix, or Routh-Hurwitz matrix, is a structured real square matrix designed with coefficients of a real polynomial.

Hn is the Hurwitz n*n matrix where 1st and 2nd rows are the even and odd co- efficients of D(s) respectively and in the remaining rows 1st and 2nd rows values will be repeated by shifting one position [6].

Bn is the n*n matrix where the first row of the Hurzwitz matrix is replaced by the coefficients of N(s)N(-s), while the remaining rows are unchanged [6].

From the above process we have obtained K1=10.07 and K2=194.615 respectively.

COMPARATIVE RESULT ANALYSIS

The relative step response analysis for the above mentioned two transfer functions is done to establish the system stability. The different parameters of these responses are also verified to analyse the optimum case.

A. CASE I

For k1=10.07, the step response shows below:

The step response shown in fig. 5 passes through unit value. So, the system is stable. The control parameters values for this case are enlisted in table I.

B. CASE I

For k2= 194.615, the step response shows below:

The step response shown in fig. 6 passes through unit value. So, the system is stable. The control parameters values for this case are enlisted in table II.

The step responses shown in fig.5 and fig.6 prove both the systems are stable.In comparison, the control parameters values depicted in table I and table II show that the 2nd transfer function is better in terms of rise time,settling time. Hence,the 2nd model is the more optimum one in this study.

CONCLUSION

This work implies the analysis for the optimum transfer function formation of prosthetic arm control model with the support of control technology. The focus is made for finding the appropriate gain value through optimal control technique.As a result, the 2nd transfer function is more effective because of its fastest response .In future, the controllability, and the adaptability aspect will introduced in this system. Also discrete domain analysis and the hard ware implementation will be the future developmental approach. The work will build a shape for the welfare of society with the development aspect of handicap human beings.

ACKNOWLEDGMENT

We want to convey our sincere thanks to Dr. Biswarup Neogi for his valuable suggestions and time for the entire work.We are grateful to Narula Institute of Technology and ECE department for their support.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3

Figure 4	Figure 5	Figure 6

References

Datta D, Brain N, “Clinical application of myo electrically-controlled prostheses” Crit Rev Phys Rehabil Med, vol. 4, no. 3-4, pp. 215- 239,1992.
Scott RN, Parker PA, “Myoelectric prostheses: State of the art”, J Med Eng Technol, vol. 12(4), pp. 143-151, Jul-Aug 1988.
Neogi B., Ghosal S., Darbar R., Ganguly S., Brahma B., “Approach towards the characteristic interpretation of Electromyography (EMG) signal with clinical study”, Recent Advances in Intelligent Computational Systems (RAICS), IEEE, pp. 788-791, Sept. 2011.
Biswarup Neogi, Sourav Mandal, Swati Banerjee, Achintya Das and D.N.Tibarewala,” Design Of Prosthetic Arms Control Transfer Function With The Analysysis In Digital Domain Inroducing Simulation Aspect”, International J. of Engg. Research & Indu. Appls. (IJERIA) ISSN 0974-1518, Vol.3, No. I , pp 260-274, 2010.
Swati Banerjee, Soumyendu Bhattacharjee ,Avishek Nag, Sreya Bhattacharyya,Dr. Biswarup Neogi, “Discrete Domain Analysis Of Dexterous Hand Model By Simulation Aspect”, C3IT-2012, Procedia Technology Vol.4 pp. 878 – 882, 2012.
Guang-Ren Duan ,Ron J. Patton, “A Note on Hurwitz Stability of Matrices”, Volume 34, Issue 4, pp. 509–511, April 1998.
Neogi Biswarup & Das Achintya ,(2008) “Recursive Method Introduce In Prosthetic Control Transfer Function” , ICSCI 2008 International Conference on Systemics, Cybernetics and Informatics, Vol.1 of 2, pp. 346-350, 2008.