Comparative Study of Different Variable
Truncated Multipliers

Athira Prasad; Robin Abraham

Comparative Study of Different Variable Truncated Multipliers

Athira Prasad¹, Robin Abraham²

Ilahia College of Engineering and Technology, Kerala, India¹
Ilahia College of Engineering and Technology, Kerala, India ²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Multipliers play a significant part in the DSP architecture. Truncation helps in the reduction of power consumption by disabling a portion of the partial product. In this paper different multipliers are made to truncate the partial products variably using a control bit and then compared for power and delay. The comparison results show that the Dadda multipliershows a small improvement in power and Baugh Wooley multiplier is better in terms of delay

Keywords

Truncated Multiplier,Baugh Wooley Multiplier, Variable Truncation, Dadda Multiplier

INTRODUCTION

Multipliers have become inevitable with the advancement of communication. Inorder to enable the implementation of complex algorithms in DSP architectures the advancing VLSI play a significant role. High speed, Low power consumption, layout regularity, reduction in area, time and delay are the major concerns while implementing multipliers which represent the backbone of a DSP system.

Multipliers developed are mainly of fixed width ie; for a N x N bit multiplication, the output attained is 2N bit product. Thus we know that we can have only a fixed width output and cannot control the length of the bits. Inorder to control the length of the bits according to the precision, required for the application, we can make the fixed width multipliers to variable truncated multipliers.

Truncation is the process of disabling or skipping a portion of the partial product to reduce the consumption of power. This process is merely a cut-off digit.In this paper different fixed width parallel multipliers are modified to multipliers with variable truncation and they are compared for power, and delay.

The Paper is designed as follows. Section II presents the Baugh Wooley multiplier, section III presents the modified Baugh Wooley multipliers which has slight modification from the earlier described Baugh Wooley multiplier. Section IV presents the dadda multiplier and Section V briefly describes the comparisons and simulation results of the different variable multipliers.The final section VI represents the conclusion.

BAUGH WOOLEY MULTIPLIER

A. Two’s Complement Multiplication

This requires an N-bit fractional multiplicand and an N-bit fractional multiplier as the inputs of the multiplier.Consider

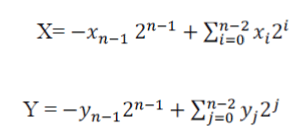Where X and Y are the multiplier and multiplicand and xi, yiÃÂÃÂµ 0,1.

The 2N-bit product will be maintained in full precision as

P = X x Y

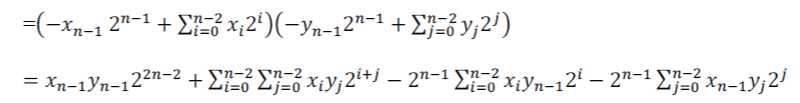Applying Baugh Wooley algorithm [7] to the partial product matrix generates results of all-positive partial product bits in a final matrix such as

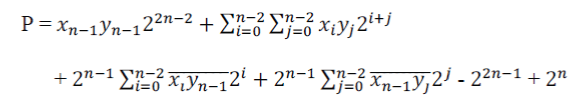When the partial product matrix of the parallel multiplier is obtained, the final product result can be generated by combining the partial product. The basic structure for a 5 x 5 bit multiplier is shown in Fig.1.

B. Truncated Multipliers

Truncated Multiplier has the advantage of reducing power consumption in the DSP systems[5],[6]. It is most commonly used in systems where least significant part of partial product can be skipped or disabled which leads to low power consumption, area and timing. Here the partial product is split into two sections namely the Least Significant Part (LSP) and Most Significant Part (MSP)[8]. The LSP is disabled or avoided to get the truncated output. The product of a full-width Multiplier can be described as Pfull = SMSP + SLSP, where SMSP represents the sum of the partial product bits belonging to the MSP and SLSP is the sum of the bits belonging to LSP. Generally, the output of the fixed-width N x N truncated multiplier is represented as Pfull-rounded = tN (SMSP + SLSP + LSB/2), where LSB represents the Least Significant Bit and tN (x) represents the truncation of an operand x by eliminating its lowest bits. Bits are discarded to maintain bit-width of N-bits

C. Variable Truncated Multiplier

Variable Truncated Multiplier [1] effectively helps in adjusting the output width of the multiplier. This follows a column based strategy which flexibly truncates the partial product as per the requirement thus controlling the power and time constraints. Truncation may be different for different applications. This architecture is flexible and work differently for different applications. The applications may differ from each other as some may require a high precision output and some others may require low power, time or area. Thus Variable Truncated Multiplier can be employed as a general purpose multiplier. The concept of the Variable Truncated Multiplication for an 8 x 8 bit multiplier is illustrated in Fig.2. The general representation of the resultant of variable truncated multiplier isP_VTM=2 where represents the control bit and represents the partial product matrix. Partial product terms for the Baugh Wooley implementation is

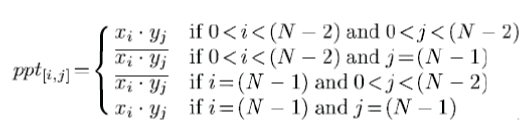Where xiand yj represents the input bits of the multiplier, X and Y. In this the 2-input AND gate is replaced with the 3-input AND gate in which the third input is the control bit t_i+j . This helps in attaining column-wise controllability which inturn makes the fixed-width multiplier a variable multiplier. To obtain a full precision multiplier all the bits within t is made to be 1 i.e. the control bit t = 0x7FFF and inorder to obtain a half partial product matrix the value of t = 0x7F00.

MODIFIED BAUGH WOOLEY MULTIPLIER

Conventional Baugh Wooley architecture makes use of AND and NAND gates. This gates can be replaced with OR and NOR gates [4] which is possible by applying the DeMorgan’s theorem.

DeMorgan’s law states that (A+B) = (A.B)

(A.B) = (A+B)

By applying the DeMorgan’s law we find that the inputs given for the OR operation is the complement of that given for the AND operation. Fig. 3 shows the modified structure of Baugh Wooley architecture. This multiplier is made variable by adding a control bit similar to that used in the variable Baugh Wooley architecture. The two input OR and NOR gates makes use of a bit the control bit which helps in controlling the truncation. When compared to AND/OR gates which make use of 6 transistors for the architecture, the NAND/NOR gates use only 4 transistors.

DADDA MULTIPLIER

Dadda multiplier, which consists of three stages,belongs to the group of fastest multipliers. The first stage generates the partial product matrix using N2 AND gates. The 8 x 8 Dadda Multiplier dot diagram is represented in Fig.4. Each dot denotes the partial products [2],[3]. The partial product is reduced to a height of two in the second stage. This stage uses thecolumn compression procedure. When the matrix is being reduced to two, a 2N-2 adderis used to obtain the final product.The steps involved in the Dadda multiplier is the same as that is used in the conventional Dadda multiplier. In the modified Dadda multiplier a control bit is added to obtain variable truncation. The procedure involved in obtaining the result is as follows

ÃÂ¯ÃâÃÂ· Let k1 = 2 and repeat kj+1 = floor (1.5 x kj) for increasing values of j. kj is the height of the matrix for the jth stage. This step is continued until the largest j is reached where there exists at least one column in the present stage of the matrix with more dots than kj. Using this equation we get k1=2, k2=3, k3=4, k4=6, k5=9 and so on.

ÃÂ¯ÃâÃÂ· Every column having heights greater than kj, are reduced to a height of kj using either half adder or full adder.

ÃÂ¯ÃâÃÂ· The reduction procedure comes to halt if the height of the matrix becomes two.

COMPARISON AND SIMULATION RESULTS

Baugh Wooley Multiplier, Modified Baugh Wooley Multiplier, Dadda Multiplier modified to variable truncated multipliers were compared for their power and delay and the result is shown in Table I. The simulation was performed using ModelSim SE PLUS 6.2b and synthesis results were obtained from Xilinx 12.3.

CONCLUSION

In this paper various fixed width multiplier architectures were made variable truncating multipliers. The comparison results show Dadda multiplier exhibits a small improvement in power and Baugh Wooley multipliers exhibit smaller delay.

Tables at a glance

Table 1

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

Manuel de la Guia Solaz, Richard ConwayandWeiHan,”A Flexible Low Power DSP With a Programmable Truncated Multiplier” IEEE transactions on circuits and systems—I : regular papers, vol. 59, no. 11, November 2012
M. Schulte, J. Stine, and J. Jansen, “Reduced power dissipation through truncated multiplication,” in Proc. IEEE Alessandro Volta Memorial Workshop Low-Power Design, 1999, pp. 61–69.
W. J. Townsend, E. E. Swartzlander, Jr., and J. Abraham, “A comparison of Dadda and Wallace multiplier delays,” in Proc. SPIE Symp.Adv. Signal Process. Algorithms, Archit., Implementations, San Diego,CA, 2003, vol. 5205.
Ronak Bajaj, Saransh Chhabra, Sreehari Veeramachaneni and M B Srinivas,”A Novel, Low-Power Array Multiplier Architecture”, International Institute of Information Technology-Hyderabad and Birla Institute of Technology and Sciences (BITS) Pilani, Hyderabad Campus
P.C.Franklin, M.Ramya,”Resource Efficient Reconfigurable Processor for DSP Applications,”International Journal of Innovative Research in Science, Engineering and Technology,Volume 3, Special Issue 3, March 2014
L.-D. Van and J.-H. Tu, “Power-efficient pipelined reconfigurable fixed-width baugh-wooley multipliers,” IEEE Trans. Comput., vol. 58, no. 10, pp. 1346–1355, Oct. 2009.
Baugh-Wooley Multiplier. [online]. Available : http://www.ece.uvic.ca/~fayez/courses/ceng465/lab_465/project2/multiplier.pdf
Truncated Binary Multipliers with minimum mean square error:analytical characterization,circuit implementation and applications byValeriaGarofalo,[online].Available:http://www.fedoa.unina.it/3904/1/Garofalo_Thesis.pdf.