ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Shweta Khare1, Vijay Prakash Singh2 , Sunil Kumar Soni3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper a mathematical method is presented to express the outage probability for a desired radio signal received from a mobile transmitter in the presence of single or multiple interfering signals with rician and Rayleigh fading. In contrast to previously reported analysis, this paper compares the outage probability & signal power at different fading environment. This is useful in determining the spectrum efficiency and performance of (interferencelimited) radio networks for cellular telephony, two-way paging, and another mobile data networks. For this analysis the interference may be single or multiple. In this paper we focus on the different parameters for output value of the different signals.
Keywords |
||||||
| Outage probability, Rician Channel, Rayleigh Channel, Interferences. | ||||||
INTRODUCTION |
||||||
| In mobile communication , the quality of service is often expressed in terms of the outage probability experienced by subscribers near the boundary of the service area of a base station. Due to limited spectrum availability, radio networks become more and more limited by mutual interference between subscribers. Received signal at the receiver is affected due to reception of no. of multipath signals. These Signals are Rician-faded & the co-channel interferers are modeled to be Rayleigh-faded. This paper is based on the consideration that a direct line-of-sight signal component exits in withincell transmission, while the interferers are assumed to be Rayleigh-faded because a direct LOS path between co-channel cells is improbable to exist. Closed-form outage probability statements are derived for both single and multiple interferences. | ||||||
| The performance analysis of mobile systems is reported in numerous research papers. Since microcells provide enhanced spectrum efficiency and economical power of handhelds, recently researchers have turned their attention to work over outage probability and spectrum efficiency of microcellular radio . In the outage probability is evaluated, assuming the desired signal as Rician fading, and considering interfering signals as Rayleigh distributed without in view of the path-loss law. The spectrum efficiency is calculated in [7], considering both desired and interfering signals as Rician faded. | ||||||
SYSTEM MODEL |
||||||
| We assume the limiting source of performance degradation [1]; therefore, for simplicity, we reject the thermal noise in our system model and consider only an interference limited environment. The transmitted signals from the desired and the interfering subscriber are, | ||||||
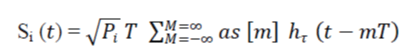 |
||||||
| where hT is transmitter pulse response, 1/T is the data transmission rate, and Ps and Pi are the transmitting powers of the desired and the ith interfering signals, respectively | ||||||
OUTAGE PROBABILITY FOR RICIAN FADING ATMOSPHERE |
||||||
| Outage probability is a key figure of merit in wireless communications. In interference-limited systems, outage probability is commonly defined as the probability that the signal-to-interference ratio (SIR) of a received signal is below a given threshold. In this part, we obtain a closed-form expression for this case. | ||||||
Derivation of Outage Probability for Rician Fading Channels |
||||||
| Let ïÿýïÿýïÿýïÿý (k = 0,……, L) be a set of independent complex Gaussian random variables, with mean value ïÿýïÿýïÿýïÿý and variance ïÿýïÿý0 2 . Let ïÿýïÿý0 represent the desired Rician signal and ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý=1 represent the sum of L Rician interferers. The outage probability for L interferers is expressed as | ||||||
| Where | ||||||
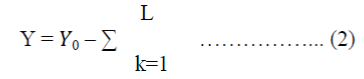 |
||||||
| And Y0=|x0|2 and Yk = RI|Xk|2; k =1, …….……L. | ||||||
| Here, RI is the signal to interference protection ratio. To derive P(outage|L) given in (1), it is necessary to find the probability density function of Y . For this, it is convenient to find the characteristic function of Y. Turin has evaluated the characteristic function of a set of N complex Gaussian random variables. In our case, we need to adopt Turin’s result, but only for each of the (k = 0….…L), we have | ||||||
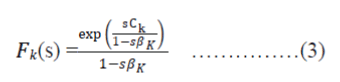 |
||||||
| Where C0 =|m0|2, 0=0 Ck,= RI|Xk|2, βk =RI , k= 1,……,L. It is noted that C0 and β0 respectively, the average power of the specular and diffused components of the desired Rician signal, whereas Ck and βk are, respectively, the average power multiplied by the protection ratio of the specular and diffused components of the interferer. Now, assuming that all the signals Xk are independent the characteristic function, F(s) of Y is given by | ||||||
| If we assume further that all the interferers have the same mean mk = mI and the same variance k = which also implies that the Rice factor of each of the interfering signals is the same, kI = |mI|2/ , then | ||||||
| The pdf of the sum of the interferers YI = ΣLk=1Yk where is defined in (2), can be obtained as the inverse Fourier transform of [ Fk[(s)L]. The inverse Fourier transform of was obtained by Bello , who applied the result of Campbell and Foster. The result is shown below: | ||||||
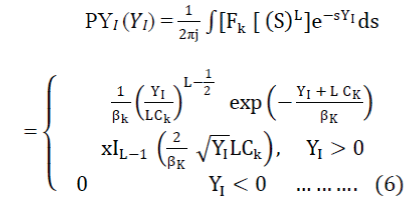 |
||||||
| The pdf of the desired signal is a special case of (6), with L = 1 and K = 0: | ||||||
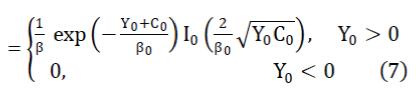 |
||||||
| Where (xïÿýïÿý) is the modified Bessel function of the first kind and order m. The pdf of Y and p(Y), defined in (2), can be found by convolving (6) and (7). The outage probability is then | ||||||
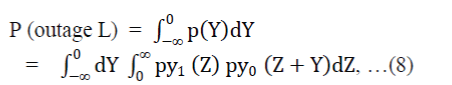 |
||||||
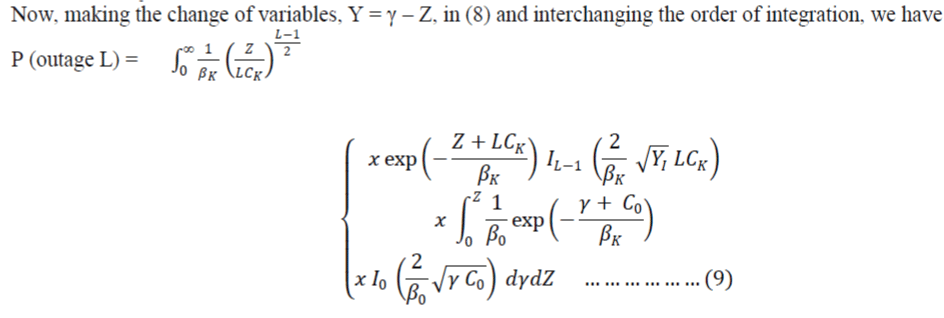 |
||||||
| Again, making the change of variables | ||||||
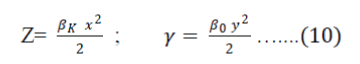 |
||||||
| In (9) by defining the parameters | ||||||
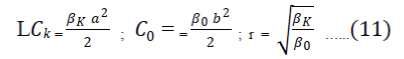 |
||||||
| Where a2/2 = kIL and b2/2 =k 0 = Rice factor of the desired signal, we arrive at | ||||||
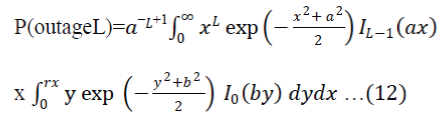 |
||||||
| The double integral is a special case of the integral evaluated by Price [9, eq. (2.5)]. Using [9, eq. (3.23)] and [9, eq. (3.24)], the new closed-form expression of the outage probability for the Rician fading channel is found to be | ||||||
| P (outage L) | ||||||
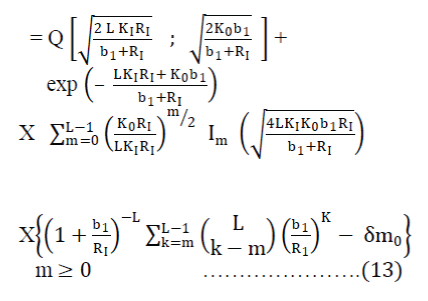 |
||||||
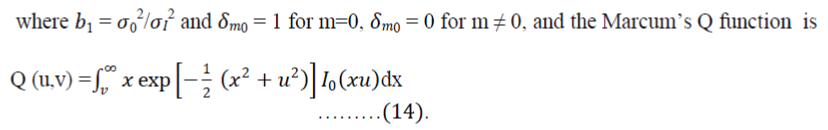 |
||||||
DERIVATIONAL RESULTS FOR DIFFERENT CASES |
||||||
| 1) In first case if we assume that Desired Signal is the Rayleigh Signal and Single Rician Interferer, and L = 1 and 0 = 0 then according to equation (13) | ||||||
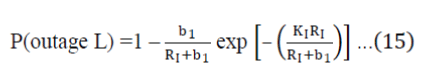 |
||||||
| 2) In second case if we assume that Desired Signal is the Rician Signal and Single Rayleigh Interferer, and kI= 0 and L =1, then according to equation (13) | ||||||
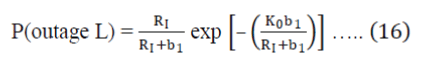 |
||||||
| 3) In third case if we assume that Desired Signal is the Rician Signal and Single Rician Interferer and L =1, then according to equation (13) | ||||||
| P (outage L) | ||||||
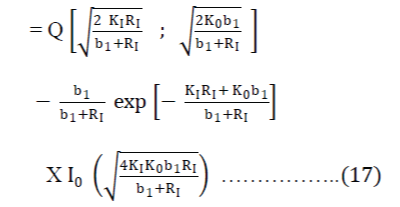 |
||||||
| In equation (13), we have assumed that all the interferers have the same mean mk = mI and k = 1,...,L. If all the interferers have distinct means , but with identical variance the Rice factors of the L interferers are distinct with Kk= mk and k = 1,…,L.. | ||||||
| In equation (6) and (9), we now have the parameter =1 instead of . Note that this holds, even when some of the interferers are Rayleigh-faded, i.e., Kk = 0, for certain k . Consequently, the outage probability for the case, where all the interferers have distinct means with the parameter LKInow being substituted by Σ Lk=1 Kk. We can see that the outage probability for this case is dependent on the sum of LOS power components of the L Rician interferers. | ||||||
COMPUTATIONAL RESULTS FOR DIFFERENT CASES |
||||||
| Figs. 1 and 2 show the outage probability graphs as a function of the signal-to-interference power ratio (SIR), and defined as | ||||||
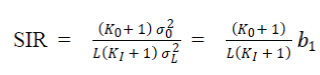 |
||||||
| It is to be noted that when comparing the curves of single and multiple interferers, for a given SIR, and given and and the value of L is then fixed. Therefore, for the larger L value, the corresponding is smaller. This means that the power of the single interferer is distributed among the L interferers. In fig 1, Outage probability curves for RI= 5 and for various values of K0,KI and L are shown. | ||||||
| By comparing the curves for K0 =KI = 10, with L = 1 and L = 6, it can be seen that when the power of a single interferer is distributed among L interferers, a lower P (outage/L) can be expected. At the other extreme, when the desired signal is Rayleigh-faded and the interferer is Rician faded (k0= 0and KI=5) the P (outage/L) is much larger than the other previous curves. | ||||||
| Fig. 2 shows the effect of different RI and L on the outage probability for Rayleigh signal. According to graph the outage probability increases as RI increases. It can also be seen that a larger L gives a smaller outage probability, as observed in Fig. 1. | ||||||
| Fig. 3 shows the effect of different RI and L on the outage probability at KI=0 for Rician signal. According to graph the outage probability is similar to the Fig. 2. | ||||||
CONCLUSIONS |
||||||
| In this paper, a novel exact derivation has been presented to compute outage probabilities due to interference in mobile radio channels with Rayleigh/ Rician fading, We have also presented different graph form of outage probability for the Rician and Rayleigh fading environment without considering any type of shadowing effect on microcellular mobile radio systems. The effect of Signal to Interference ratio (SIR), Protection ratio (RI), Rice factor of signals K, and number of cochannel interferes L on the outage probability have been investigated. New Rician/Rayleigh outage probabilities graphs for different values of protection ratios are presented and discussed. The results are almost same as previous results by this technique. | ||||||
Figures at a glance |
||||||
|
||||||
References |
||||||
|