International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparison of Conventional Controller with Model Predictive Controller for CSTR Process

S.Allwin1, S.Biksha natesan2, S.Abirami3, H.Kala4, A.Udhaya prakash5
  1. Assistant professor, Department of ICE, Saranathan Engineering College, Trichy, Tamilnadu, India3, 4
  2. UG Student, Department of ICE, Saranathan Engineering College, Trichy, Tamilnadu, India1, 2, 5
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

We designate PID (Proportional Integral Derivative) controller in industries for various process control applications. It provides control action to the discrepant values from the desired values in process output. CSTR (Continuous Stirred Tank Reactor) is the most important process which plays a significant role in process and chemical industries. We have to control various process variables like temperature, concentration, flow, pressure etc. in this process. Hence we need appropriate control action to maintain this process in the desired condition. We use PID controller which yields an overshoot and long settling time, which exacerbate the process. Hence it is not well suited for many complex processes in industries. So we are going for a better type of controller, known as MPC (Model Predictive Control). It is very accurate and reliable in controlling the process variable. MPC has the ability to anticipate the future events and takes action accordingly. In this manuscript comparison of PID controller with MPC is made and we examine the best controller for this CSTR temperature control process.

Keywords
Continuous Stirred Tank Reactor, MPC controller, PID controller, CSTR temperature control process.

INTRODUCTION
Normally CSTR process is very complicated in nature and deals with multiple aspects in industries [1]. It consists of more than one process variables and manipulated variables. All the variables in this process are correlated. Any changes in the single variable lead the system to undesirable behaviour [4]. We have to control all the variables based on their relationship between them for controlling the system in a desired value. In industries, they use cascade controller for getting more accurate control action for this process [6]. PID controller plays a crucial role in industries [2]. Due to its demerits we are going for new type of controllers.
Designing a controller to this process is very complicated and big challenge for engineers [10]. Many process and chemical industries uses this CSTR process. There they have to use lots of controller for maintaining the process in desired condition. So we need to use more than one sensor for measuring each parameter from this process. The measured physical variable in this process can be used for designing the controller [8]. In this paper, we are going to find out which controller is going to give an appropriate control action for this CSTR temperature control process. By comparing the controllers one with another, we can finalise the result based on the performance index and time domain specifications [3]. Every controller behaves on its own way in maintaining the process into a desired value.
In the previous paper, they told that we get good performance for the CSTR temperature control process using 2 DOF PID [2]. They are using 2DOF PID controller for this process. It gives satisfactory result to the engineers. In another paper they told that they are getting better solution for the CSTR temperature control process by using polymath programming [3]. They finalised the result using this polymath programming method.

CSTR PROCESS
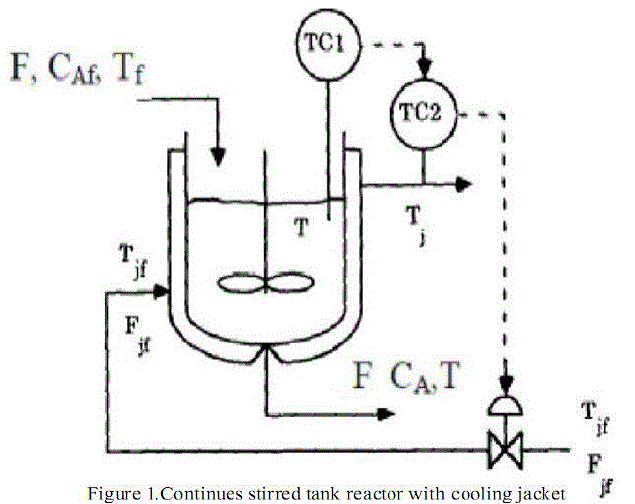
Continuous stirred tank reactor (CSTR) is a one which is used in various chemical and process industries [3]. It is also called as vat or back mix reactor [5]. The reactants are continuously fed into the reactor. The reactant is mixed perfectly for getting product in chemical industries. For getting perfect reaction by this process, we must control all the process parameters in desired values [6].
We are going to derive the mathematical model of the CSTR temperature control process. Here the reactor surrounded by a jacket with coolant with lower temperature than reactor, which is used to diminish the temperature of the reactor [1]. The flow of coolant around the jacket determines the process temperature. Here controlled variable is temperature of process and only manipulated variable is flow of coolant in the jacket.

PROCESS PARAMETER
All the systems are identified based upon their behaviour of various dynamic inputs applied to it. The dynamic behaviour of the system for various inputs is known as SI (System Identification). From the true behaviour of the system for various inputs, we can derive the mathematical model of the system [7]. For deriving the mathematical model of the system, first we have to choose process variable from the process and then we need to write mass and energy balance equation from the given setup. Mathematical model theoretically represents the behaviour of the system for different inputs. It helps us to steady about the behaviour of the system theoretically before implementing it [9]. Engineers design the controller for the system by using its mathematical modelling. Another way of finding system behaviour is pragmatic designing [7]. We get the behaviour of the system by designing the system pragmatically. As per our anticipation about the process response for various inputs using mathematical modelling, we get the same desired response for implementation of the process pragmatically for the same inputs [8]. This process consists of more than one process variable. So it is a second order system, the basic second order equation is,
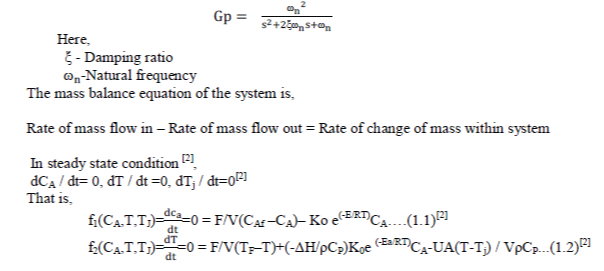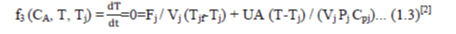image
image
Reactor parameter’s value:[1]
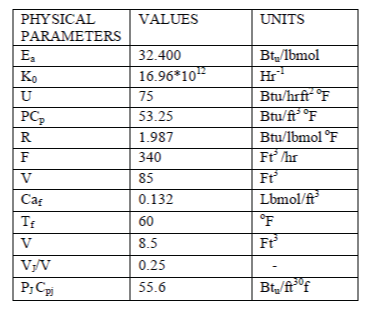image
These are all the values taken from the model of the CSTR temperature control process. By substituting these values in general equation we get the resultant equation from the above derivation in the form of state model [1],
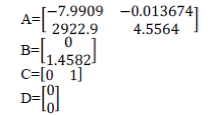image
By using state space model to transfer function conversion statement in MATLAB, we get the transfer function [t / tf] of this process [1].
image
This is the mathematical model of our CSTR temperature control process, which has been derived from the pragmatic modelled system.

CONTROLLER DESIGNING
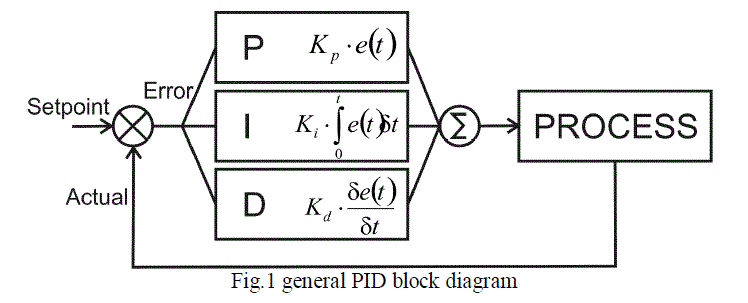
A.PID CONTROLLER:
Simulation of the CSTR temperature control process has been done by using its mathematical modelling in MATLAB. The image of the simulated block diagram of the CSTR temperature control process consists of step input, PID controller, system and scope for visualize the output response.
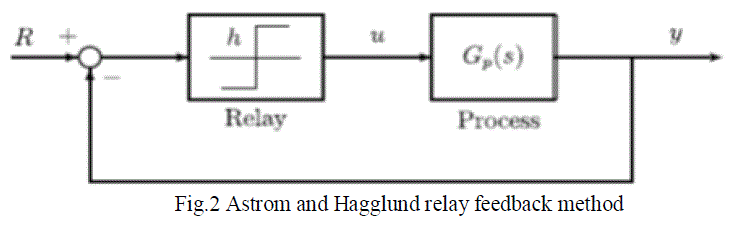
The designing of control parameters for this process is done by various methods. For designing the controller we need to know about the system response. We apply Astrom and Hagglund relay feedback logic to find the system response [1]. We have to replace the PID controller with relay for finding the Kp and Pu.
We find the Kp and Pu values by using this relay feedback logic in MATLAB for tuning the controller.
This figure 1.3 represents the model of for Astrom and Hagglund relay feedback logic. Here the relay is used for maintain the process variable in the set point. It will hold until the process variable reaches its set value. After exceeding the desired value it switches the process variable to its negative set value and begins to hold its activity. This process repeats continuously for a long time in the same interval. Whenever there is a small error in the system or the output lags input by π radians, the system will start to oscillate with period of Pu.
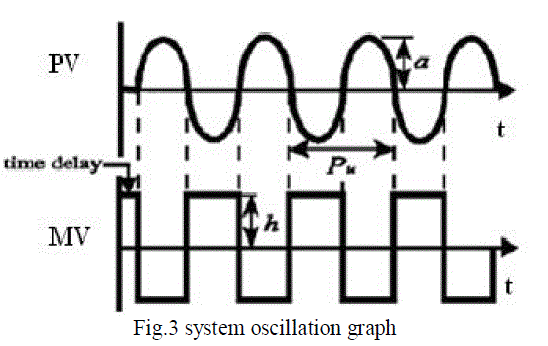
Figure 1.4 shows that how to get the Kp and Pu values from the response curve. Here ‘a’ is amplitude of process response curve, Pu is a period of process variable oscillations and h is magnitude of manipulating variable. We take the Ku and Pu values from the response curve. The period of oscillation is 2 sec and gain is 1.4. By using these values we design the controller.
Ziegler-Nichols Tuning method:
This method is a trial and error tuning method based on sustained oscillations which was first proposed by Ziegler and Nichols (1942). This is probably the most widely used method for tuning of PID controller and is also known as online or continuous cycling or ultimate gain tuning method. Having the ultimate gain and frequency (Ku and Pu) and using table 1.1, the controller parameters can be obtained.
By using this formula, we can find the control parameter. Put this values in general controller equation.
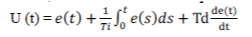image
After substituting these values in equation, we simulate the process in MATLAB. It gives the response to the discrepant values of the given CSTR temperature control process.
Chien-Hrones-Reswick Auto tuning Method:
It is another method of designing a PID controller. It is an efficient method and is used to get the precise control action to error value. It has four types of formula for designing a controller. By knowing the value of dead time and time constant we calculate the controller parameters. The following tables show the Chien-Hrones-Reswick recommendations for each tuning formula:
Where TP is the time constant and is the dead time.
Where TP is the time constant and is the dead time.
Where TP is the time constant and is the dead time.
Where TP is the time constant and is the dead time
After substituting the controller parameter values in the general equation, we have simulated the setup.
Tyreus-Luyben Tuning Chart:The Tyreus-Luyben procedure is quite similar to the Ziegler-Nichols method but the final controller settings are different. Also these methods only propose settings for PI and PID controllers. These settings are based on ultimate gain and period is given in the table 1.6.
After finding the controller parameter, we substitute those values into the general equation, then simulate the process in the MATLAB which gives us the response curve.
From the above strategy we finalised the best controller for our process. But we already know that, PID controller has overshoot and long settling time.Hence now we are going for new type of digitalised controller, known as MPC (Modern Predictive Control).
B. Model Predictive Control:
Modern predictive control is a digital control which is used in chemical and process industries for solving complicated processes since 1980’s. It needs process parameters to control the process in desired value, which has been obtained pragmatically by modelling the process. It keeps future time slots into an account and allows the current time slot to be optimized. MPC can anticipate future events and takes control actions accordingly. But PID controllers and others cannot predict the future events.
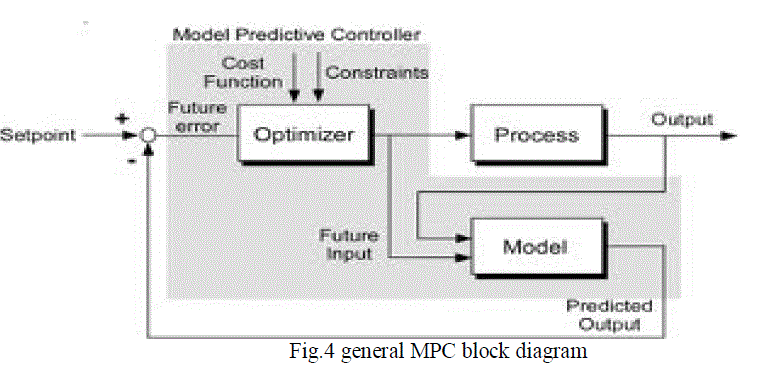
Model Predictive Control (MPC) is a multivariable control algorithm that uses:
an internal dynamic model of the process
a history of past control moves and
an optimization cost function J over the receding prediction horizon,
The optimization cost function is given by:
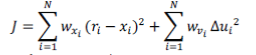image
th controlled variable (e.g. measured temperature
th reference variable (e.g. required temperature)
th manipulated variable (e.g. control valve)
weighting coefficient reflecting the relative importance of
weighting coefficient penalizing relative big changes in
This is the block diagram of modern predictive controller used in MATLAB for simulating the mathematical model of the process. We configure MPC depends upon the process parameters. It gives as a satisfactory control action to the process compared with conventional controller. MPC has better control ability over the deviation of the process variable.

RESULTS AND DISCUSSIONS
From the above controller designing method, we got various types of response for each controller. These responses provide us a sufficient knowledge about the response of the system for different controller. We tabulated the time domain specifications and performance index values below.
TIME DOMAIN SPECIFICATIONS:
Above table1.7 shows the performance of the different controller action upon our CSTR process. Different controller has different settling time and overshoot. From these results we find out which controller will be best for our process. From these values we find that Z-N based PID controller is well suited for our CSTR process among the conventional controller. But we are considering the model predictive controller, it will be the best one for our process. It has short settling time and lower overshoot percentage.
PERFORMANCE INDICES:
In this time domain specification and performance criteria, we select the best controller by considering the minor overshoot and settling time into an account. The comparative analyses of diverse controllers are shown in below figure. This performance index gives as the possibilities of error during the process for different controller. Minimum ISE and ITAE value gives the better controller action for the process.
Comparison chart has different controller performance and its step response. From this chart we identified that MPC controller has better performance over our process. Compared with other conventional controller, MPC has minimum overshoot and settling time.

CONCLUSION
From the above discussion, we identified the best controller for CSTR temperature control process to be MPC. For controlling temperature in a constant value it is very complicated in industries. MPC controller leverages these difficulties by bringing the process variable to the desired set point as quickly as possible. Even though MPC controller is not suitable for a simple system, it is good for a complicated system like our CSTR temperature control processes. MPC controller has a 0% overshoot and minimum settling time as compared with other conventional controller that we used in this process. So we can consolidate the performance of all of these responses and we finalised the result as MPC is the best controller for our CSTR temperature control process.

Tables at a glance
Table icon Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4 Table 5
Table icon Table icon Table icon
Table 6 Table 7 Table 8
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References