International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparison of Digital Image watermarking Methods DWT & DWT-DCT on the Basis of PSNR

Navnidhi Chaturvedi1, Dr.S.J.Basha2
 M.Tech Scholar, Lakshmi Narayin College of Technology, RGPV University, Indore, Madhya Pradesh, India1
Department of ECE, Lakshmi Narain College of Technology, Indore, Madhya Pradesh, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The authenticity & copyright protection are two major problems in handling digital multimedia.The Image watermarking is most popular method for copyright protection by discrete Wavelet Transform (DWT) which performs 2 Level Decomposition of original (cover) image and watermark image is embedded in Lowest Level (LL) sub band of cover image. Inverse Discrete Wavelet Transform (IDWT) is used to recover original image from watermarked image. And Discrete Cosine Transform (DCT) which convert image into Blocks of M bits and then reconstruct using IDCT. In this paper we have compared watermarking using DWT & DWT-DCT methods performance analysis on basis of PSNR, Similarity factor of watermark and recovered watermark.

Keywords
DWT, DCT, Cover Image, Watermark, Watermarked Image

INTRODUCTION
Digital Image Watermarking is a technique which provide solution for Copyright, image authentication and other issuesWatermarking deals with decomposing original image called Cover image using some wavelet Transforms[1] and embedding watermark into one of the sub band (LL,LH,HL,HH) the obtained image is called watermarked image (Stego Image) this image have transmitted throught Channel Where various noise Affect watermarked Image [2],[3],[4].At receivers Side embedded watermark has extracted from watermarked image[5].For watermark embedding Discrete Wavelet Transform(DWT) has used, DWT is a Wavelet Transform which use Dydic Filters to decompose M×N Image in to N-Levels, we can embed watermark into one of the sub band, For Extraction of Watermark Inverse Discrete Wavelet Transform (IDWT) is used[6] Commonly used frequency-domain transforms include the Discrete Wavelet Transform (DWT), the Discrete Cosine Transform (DCT) and Discrete Fourier Transform (DFT). However, DWT[7] has been used in digital image watermarking more frequently due to its excellent spatial localization and multi-resolution characteristics, which are similar to the theoretical models of the human visual system[8]. Further performance improvements in DWT-based digital image watermarking algorithms could be obtained by combining DWT with DCT[9]. The idea of applying two transform is based on the fact that combined transforms could compensate for the drawbacks of each other, resulting in effective watermarking. In this paper, we will describe a digital image watermarking algorithm based on comparing two methods; DWT and DWTDCT. Watermarking is done in DWT by level1 decomposition & calculating the wavelets coefficients of carefully selected DWT lowest sub-bands, in case of DWT-DCT method level1 decomposition of cover image & calculating the wavelets coefficients of carefully selected DWT lowest sub-bands followed by the application of the DCT transform of Watermark on the selected LL sub-bands.Analysis of Image has based on Performance Parameters like Signal to Noise Ratio (SNR) of original & watermarked Image[7] Peak signal to Noise ratio(PSNR) & Daubichis 3 wavelet has used to analyze watermarking [15].

II-DISCRETE WAVELET TRANSFORM (DWT)
Discrete Wavelet transform (DWT) is a mathematical tool for hierarchically decomposing an image. It is useful for processing of non-stationary signals. The transform is based on small waves, called wavelets, of varying frequency and limited duration. Wavelet transform provides both frequency and spatial description of an image. Unlike conventional Fourier transform, temporal information is retained in this transformation process. Wavelets are created by translations and dilations of a fixed function called mother wavelet. This section analyses suitability of DWT for image watermarking and gives advantages of using DWT as against other transforms. For 2-D images, applying DWT corresponds to processing the image by 2-D filters in each dimension. The filters divide the input image into four non-overlapping multi-resolution sub-bands LL1,LH1, HL1 and HH1. The sub-band LL1 represents the coarse-scale DWT coefficients while the sub-bands LH1, HL1 and HH1 represent the fine-scale of DWT coefficients. To obtain the next coarser scale of wavelet coefficients, the sub-band LL1 is further processed until some final scale N is reached. When N is reached we will have 3N+1 sub-bands consisting of the multi-resolution sub-bands LLN and LHx, HLx and HHx where x ranges from 1 until N. Due to its excellent spatiofrequency localization properties, the DWT is very suitable to identify the areas in the host image where a watermark can be embedded effectively. In general most of the image energy is concentrated at the lower frequency sub-bands LLx and therefore embedding watermarks in these sub-bands may degrade the image significantly.Embedding in the low frequency sub-bands, however, could increase robustness significantly. On the other hand, the high frequency sub-bands HHx include the edges and textures of the image and the human eye is not generally sensitive to changes in such sub-bands. This allows the watermark to be embedded without being perceived by the human eye.

III- DISCRETE COSINE TRANSFORM (DCT)
The DCT transform: The discrete cosine transforms is a technique for converting a signal into elementary frequency components [9]. It represents an image as a sum of sinusoids of varying magnitudes and frequencies. With an input image, x, the DCT coefficients for the transformed output image, y, are computed according to Eq. 1 shown below. In the equation, x, is the input imagehaving N x M pixels, x(m,n) is the intensity of the pixel in row m and column n of the image, and y(u,v) is the DCT coefficient in row u and column v of the DCT matrix.
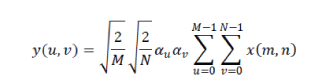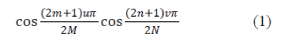image
image
Where alpha u and alpha v are given by:
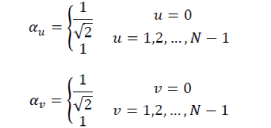image
The image is reconstructed by applying inverse DCT operation according to Eq. 2:
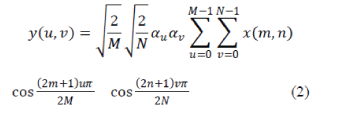image
The popular block-based DCT transform segments image non-overlapping blocks and applies DCT to each block. These results in giving three frequency sub-bands: low frequency sub-band, mid-frequency sub-band and high frequency sub-band. DCT-based watermarking is based on two facts. The first fact is that much of the signal energy lies at low-frequencies sub-band which contains the most important visual parts of the image. The second fact is that high frequency components of the image are usually removed through compression and noise attacks. The watermark is therefore embedded by modifying the coefficients of the middle frequency sub-band so that the visibility of the image will not be affected and the watermark will not be removed by compression.
a) Algorithm for DWT Gray Image Watermarking:
1. Watermark Embedding:
Watermark Embedding Process consist of decomposing Original 256×256 image into 1-level sub bands using DWT which generate Four sub-bands (LL, LH, HL, HH) out of which LL (Lowest Level) has selected for watermark embedding as it contain maximum energy .The Watermark of 128×128 is embedded into LL, Obtained image is called Watermarked Image, Figure (1) shows watermark embedding process.
2. Watermark Extraction:
Watermark extraction is a process of removing watermark from watermarked image its opposite process of Watermarking ,Inverse Discrete Wavelet Transform is used for Extraction of Watermark with Daubechies (db1)filter as shown in Figure (1).The Watermarked image is again decomposed using level 1 IDWT then DWT of image is obtained, DWT image is compared with Original image and watermark is extracted from watermarked image.
b) Algorithm for DWT-DCT watermarking
In this algorithm for watermark embedding and extraction two popular methods are combined DWT & DCT this method is explained below:
1. Watermark Embedding :
Watermark Embedding Process in DWT-DCT mehod is somehow same as DWT method of decomposing Original 256×256 image into 1-level sub bands using DWT which generate Four sub-bands (LL, LH, HL, HH) out of which LL (Lowest Level) has selected for watermark embedding as it contain maximum energy .The DCT of Watermark 128×128 is calculated and then DCT transformed watermark is embedded into LL, then Inverse DWT is calculated of obtained image, obtained image is called Watermarked Image, in order to convert time to spatial domain Figure (2) shows watermark embedding process.
2. Watermark Extraction .
For extracting watermark DWT of watermarked image is calculated and as this detection is non blind detection original and watermarked are correlated so obtain Watermark
c) Parameters Used:
For analysis of Best method out of DWT & DWT-DCT we have used PSNR and MSE ,Similarity Factor.
1. Peak Signal to Noise Ration (PSNR): PSNR is the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. Because many signals have a very wide dynamic range, PSNR is usually expressed in terms of the logarithmic decibel (dB) scale.
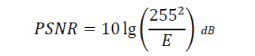image
Where E is Mean Square Error , f(i,j) is pixal value of original image f’(i,j) of watermarked image and its logarithmic unit is dB Given by Formula:
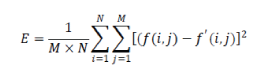image
2. Similarity Factor (SF): Similarity Factor is measure of the similarity of pixel intensities between the original image and the watermarked image. This helps us to calculate the changes in the perceptual quality of the image more precisely. The formula for SIM is shown below:
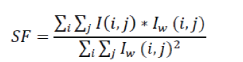image
Where I(I, j) is the original image and Iw (i, j) is the watermarked image. The similarity factor should be equal to 1.

IV- SIMULATION & RESULTS
1. DWT method:
The watermark Embedding and Extraction process has been shown in figure (1) & figure(2), Algorithms for Watermark Embedding use original (256×256) gray Image called “Cameraman” and watermark Image is also gray image (128×128) called “ watermark”. The Scaling Factor (α) of DWT lies between 0.01 to 0.09 and Quality Factor (Q) lies between 1 to 9 as shown in table (1).
Figure (5) shows the original image (gray) cameraman which is 256×256.the watermark used for embedding is shown in figure (6).
Figure (6) is a watermark image of size 128X128.which embedded in to LL sub band after decomposing. The watermarked image & extracted watermark is shown in figure (7).
2. DWT-DCT method
The watermark Embedding and Extraction process has been shown in figure (8) & figure(9), Algorithms for Watermark Embedding use original (256×256) gray Image called “Cameraman” and watermark Image is also gray image (128×128) called “ autumn”. The Scaling Factor (α) of DWT lies between 0.01 to 0.09 and Quality Factor (Q) lies between 1 to 9 as shown in table (1).
Figure (8) shows the original image (gray) cameraman which is 256×256.the watermark used for embedding is shown in figure (9).
Figure (9) is a watermark image of size 128X128.which than this watermark is DCT transformed & embedded in to LL sub band after decomposing. DCT transformed & The watermarked image & extracted watermark is shown in figure (10).

V-CONCLUSION
To siimullatte rresulltts we have used MATLAB @R2009b iin tthiis paperr we have comparred DWT& DWT--DCT metthod whose vallue fforr PSNR iis 58..39dB fforr DWT--DCT metthod and 51..466dB fforr DWT metthod so,, we have conclluded tthatt DWT--DCT metthod iis bestt ttechniique fforr llevell one watterrmarrk embeddiing.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5


Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10


Figure 11
Figure 1
 

References
  1. Nagaraj V.Dharwadkar & B. B. Amberker International Journal of Image Processing Volume (4): Issue (2) 89
  2. Determining the Efficient Subband Coefficients of Biorthogonal Wavelet for Gray level Image Watermarking International Journal of Image Processing Volume (4): Issue (2)
  3. Chu, W, 2003. "DCT-Based Image Watermarking Using Subsampling," IEEE Trans. Multimedia, 5(1): 34-38.
  4. Lin, S. and C. Chin, 2000. "A Robust DCT-based Watermarking for Copyright Protection," IEEE Trans. Consumer Electronics, 46(3): 415-421.
  5. Deng, F. and B. Wang, 2003. "A novel technique for robust image watermarking in the DCT domain," in Proc. of the IEEE 2003 Int. Conf. on Neural Networks and Signal Processing, vol. 2, pp: 1525-1528.
  6. Wu, C. and W. Hsieh, 2000. "Digital watermarking using zero tree of DCT," IEEE Trans. Consumer Electronics , vol. 46, no. 1, pp: 87-94.
  7. Digital Image Steganography:Survey and Analysis of Current Methods Abbas Cheddad, Joan Condell, Kevin Curran and Paul Mc
  8. Kevitt Zhang Guangnan, Wang Shushun. A Blind Watermarking Algorithm Based on DWT for Color Image.