International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparison of Matching Algorithms for MST Radar Data

S.DIVAKAR 1, DR. R.V.S.SATYANARAYANA 2
  1. 1M.Tech student, Department of ECE, SVU college of Engineering, Tirupati, Andhra Pradesh, India
  2. 2Professor, Department of ECE, SVU college of Engineering, Tirupati, Andhra Pradesh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Atmospheric Signal processing has lot of scope for development of new and efficient tools for Cleaning of the spectrum, detection and estimation of the desired parameters. The purpose of this project is to study the data processing techniques and the matching algorithms for the MST Radar. This project deal with signal and data processing techniques. The proposed algorithms estimate the similarities between the signatures. We evaluated the following algorithms SAD (Sum of Absolute Difference), SSD (Sum of Squared Difference), ED (Euclidean Distance) and Correlation.

Keywords
MST Radar, SAD, SSD, ED

INTRODUCTION
Radar systems send out modulated waveforms using antennas in order to transmit electromagnetic energy into a specific volume of space to search for targets. Objects (i.e. targets) within a certain volume will reflect part of the energy (radar returns or echoes) back to the radar. From these radar returns, the radar receiver then extracts information such as velocity and range, angular position, and other identifying characteristics. If relative motion exists between target and radar, the shift in the carrier frequency of the reflected wave (Doppler Effect) is a measure target’s relative (radial) velocity and may be used to distinguish moving targets from stationary objects.
1.1. Atmospheric Radar Principle:
It uses the principle of back scattering mechanism. The target of interest for the Atmospheric radars is the clear air echoes without ionisation. The primary mechanism of backscatter from the clear atmosphere is the radio refractive index fluctuation experienced by an electromagnetic wave due to the presence of localised scattering centres known as refractive index irregularities that are flowing in the background mean flow.

MST RADAR
A Mesosphere, Stratosphere, Troposphere (MST) Radar was constructed at Gadanki (13.50N, 79.20E) in south eastern part of India. MST Radar uses radio wave signals to investigate the atmospheric changes. The name itself is reflecting that it observes the changes in Mesosphere, Stratosphere, Troposphere layers of the earth atmosphere. The MST Radar makes use of the scattering and reflection from the variations of humidity, temperature and electron density, induced by the turbulence and fluctuations in the refractive index of the atmosphere.
The MST Radar is capable of providing estimates of the atmospheric parameters with very high resolution and on a continuous basis. It can operate at any time throughout the day. The main advantage with this is the providing continuous data. MST Radar uses the echoes obtained over the height range of 1-100 Km to study winds, turbulence. The main specification of the system is displayed in the Table 1. The Indian MST Radar has been operational for scientific studies of the atmosphere in the height range of 2-20 km. (troposphere and lower stratosphere), 60-90 km (mesosphere), 100-150 km (E region) and 150- 800 km (F region). India has been operating 53 MHz atmospheric radar (Mesosphere, Stratosphere and Troposphere radar) for studying structure and dynamics of lower, middle and upper atmosphere.

MATCHING ALGORITHMS
The fundamental computational operation performed by the radar system is to match an incoming live signature against a library of pre-recorded signatures. In order to evaluate different algorithms efficiently, we utilize the data collection mode of the radar for the three wind signatures. Each algorithm computes a single match value when executed on a library signature and live signature pair. The wind corresponding to the library signature that exhibits the best match with the live signature is selected. We evaluate the following algorithms.
3.1. Sum of Absolute Differences (SAD): The total difference between the two signatures is calculated by adding the absolute value of differences between the samples. The match with the smallest total difference is taken as best. The algorithm for SAD is shown in Fig 1.
3.2. Sum of Squared Differences (SSD): The total difference between the two signatures is calculated by adding the square of differences between the samples. The match with the smallest total difference is taken as best. The algorithm for SSD is shown in Fig 2.
3.3. Euclidean Distance (ED): The total distance between the two signatures is calculated by taking the square root of the sum of squared differences. The match with the smallest total difference is taken as best. The algorithm for ED is shown in Fig 3.
3.4. Correlation (C): The correlation between the two signatures is calculated by taking the average pairwise product of the samples. The match with the maximum correlation is taken as the best. The algorithm for Correlation is shown in Fig 4.

RESULTS
4.1. Power spectrums with Doppler shift of the MST Radar Data of 24/07/2013 at 3:33:30PM:
The quadrature signal components are converted from time domain to frequency domain by using Fourier transform with appropriate sampling frequency that is with Nyquist rate. From this, the power spectrum will be computed by squaring the magnitude spectrum. Further analysis will be taken from the power spectral only.The below Figures 5-10 are the power spectrums in different directions taken. The vertical axis contains the Range in Km, while the horizontal axis represents the Doppler Shift in Hz.
4.2. Moments Calculation:
The whole signal processing is done to extract the spectral zeroth, first and second moments and from the moments the total power, Doppler shift and spectral width will be obtained. From these the Doppler velocity will be computed. The Equations (1)-(3) represents the total power, Doppler shift and spectral width of the signal respectively.
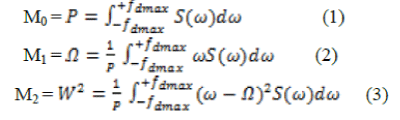image
The Figures 11(a)-(c) represents the total power, Doppler shift, and spectral width of the signal respectively.
4.3. Comparison of Matching Algorithms: The results of this evaluation are depicted in Figure 12. The vertical axis contains the percentage of correct matches, while the horizontal axis represents the varying number of signatures being averaged.

CONCLUSIONS
In this paper, the following proposed matching algorithms SAD (Sum of Absolute Difference), SSD (Sum of Squared Difference), ED (Euclidean Distance) and Correlation are evaluated for the MST Radar data. According to the Results, the algorithm with the best performance is the SAD algorithm which exhibits maximum accuracy. The SSD and ED algorithms exhibit moderate performance, and the Correlation algorithm performs poorly.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 11 Figure 12 Figure 13
Figure 11 Figure 12 Figure 13
 

References
  1. Anandan, V. K., “Atmospheric Data Processor – Technical and User reference manual, National Atmospheric Research Laboratory, Gadanki.
  2. Briggs, B. H., “Radar observations of atmospheric winds and turbulence: a comparison of techniques”. Journal of Atmospheric and Terrestrial Physics, vol.42, 823-833, 1980.
  3. Briggs, B.H., “The analysis of spaced sensor records by correlation techniques”, Handbook for MAP, Vol.13, and Ground based techniques, 166-186, University of Illinois,
  4. Doviak, R.J., and Zrnic.D.S, “Doppler radar and Weather Observations”, Acadamic Press, London 1984.
  5. Barth,M.F., R.B.Chadwick, D.W.van de Kamp, 1994:“Data processing algorithms used by NOAA‟s wind profiler demonstration network”, Ann.Geophysicae, volume 12, 518-528.
  6. Balsley, B.B. (1995), “Development of generic radar equations for wind profiling, in Diagnostics tools in atmospheric physics”, Proceedings of the international school of Physics, Enrico Fermi, Course CXXIV 22 Jun - 2 Jul., 1993, pp 69-78, IOS Press, Amsterdam.
  7. Rao. P.B., A.R. Jain, P. Kishore, P. Balamuralidhar, S.H. Damle and G. Viswanathan (1995), “Indian MST radar 1.System description and sample vector wind measurements in ST mode”, Radio Science, vol. 30, pp. 1125 - 1138.
  8. JurgenRottger (1989), “The Instrumental Principles of MST Radars and Incoherent Scatter Radars and The Configuration of Radar System Hardware”, vol.30, pp. 54-113.
  9. Sarkar, B.K., P.B. Tole, and A. Agarwal (1988), “Feeder network for the Indian MST radar”, in Handbook for MAP, edited by C.H. Liu and B. Edwards, vol.28, pp. 523-527,SCOSTEP Sect., Urbana, Illinois.