ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
I. Catherine Divya1, Dr. S. Nagalakshmi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In recent years, the electrical power demand has grown rapidly and electricity utilities are in need to serve more demand and also to maintain system security. FACTS devices reduce the flows of heavily loaded lines, maintain the bus voltages at desired levels.This paper applies Min Cut algorithm and Differential Evolution (DE) algorithm to select Optimal location of TCSC, SVC for Security Constrained Optimal Power Flow (SCOPF) under normal and n-1 contingency operating condition for pool model of deregulated power system. The proposed method includes the installation cost of FACTS devices which helps the system operators to operate the system in a more economic way. To validate the proposed approach simulations are performed on IEEE 6 bus test system. The results indicate that for optimal location and control of FACTS devices, DE algorithm is more efficient with and minimum active power generating cost as compared to Min Cut algorithm.
Keywords |
||||||||||||||||||
| Differential Evolution (DE) algorithm, Flexible Alternating Current Transmission Systems(FACTS), Min Cut algorithm, Security Constrained Optimal Power Flow (SCOPF), Static Var Compensator(SVC), Thyristor Controlled Series Compensator(TCSC). | ||||||||||||||||||
INTRODUCTION |
||||||||||||||||||
| The secured operation of power system has become an important and critical issue in today’s large, complex, and load-increasing systems. Commonly, power systems are planned and operated based on the n-1 security criterion, which implies that the system should remain secure under all important first contingencies. Hence there is a need to design the system to meet the n-1 security criterion which is conservative and costlier [1]. Better system operating conditions are achieved when sufficient security and economy are accounted which is known as Security Constrained Optimal Power Flow (SCOPF).The SCOPF is an extension of OPF problem which takes into account constraints arising from the operation of the system under a set of postulated contingencies. The SCOPF problem is a nonlinear, non-convex, large-scale optimization problem, with both continuous and discrete variables [2,3]. | ||||||||||||||||||
| As a solution to this problem, either the existing transmission lines must be effectively utilized, or new transmission lines should be added to the existing system. Environmental right-of-way and cost problems are major hurdles for power transmission network expansion. Hence there is an interest for better utilization of existing power system capabilities. Flexible AC Transmission Systems (FACTS) devices have gained a great interest in transmission system due to recent advances in power electronics. | ||||||||||||||||||
| this work optimal location of TCSC and SVC is obtained by using Mincut algorithm and Differential Evolution Algorithms. Hence Security Constrained Optimal Power Flow (SCOPF) is achieved. | ||||||||||||||||||
LITERATURE SURVEY |
||||||||||||||||||
| Various methods have been used to determine the optimal location and control of FACTS devices in transmission system for pool model. Sensitivity based approach was proposed to locate Thyristor Controlled Series Compensator (TCSC) and Unified Power Flow Controller (UPFC), considering voltage and angle sensitivities with respect to changes in the system load [4]. Continuation Power Flow (CPF) was used for obtaining the size and locations of the series compensators to increase the security of the system. This study identifies critical lines that can initiate cascading line outages and optimal location and parameter settings of series and shunt compensators [5]. Mixed Integer Linear Programming (MILP) based Optimal Power Flow (OPF) methods were used to determine the optimal location of Thyristor Controlled Phase Shifting Transformer (TCPST) for pool model [6].Population based computational intelligent techniques such as Genetic Algorithm (GA), Evolutionary Programming (EP) and Particle Swarm Optimization (PSO) were used to determine optimal location of FACTS devices for pool model. GA was utilized to simultaneously search for locations, types, and parameter settings of FACTS devices, subject to thermal and voltage limits [7]. GA was also utilized to determine the optimal location and settings of FACTS devices [8, 9]. EP was proposed to obtain optimal placement of multi-type FACTS devices for simultaneously maximizing the total transfer capability whereas minimizing the total system real power loss and the results are better when compared to loss sensitivity index method [10]. The optimal location for single and multi-type FACTS devices to improve system security was determined using PSO [11].Min cut algorithm was used to obtain optimal location of TCSC [12]. | ||||||||||||||||||
| In this paper Min Cut algorithm and Differential Evolution (DE) algorithm are applied to select proper location of FACTS device for SCOPF under normal and n-1 contingency operating condition for Pool model of deregulated power system. The objective of the paper is to obtain SCOPF solution under normal operation and n-1 contingency condition through the optimal utilization of FACTS device. The performance of Differential Evolution is validated by comparing the results with Min cut Algorithm. | ||||||||||||||||||
MODELING OF FACTS DEVICES |
||||||||||||||||||
| A. Modeling of TCSC | ||||||||||||||||||
| TCSC consists of series compensating capacitor shunted by thyristor controlled reactor. It is modeled as a controllable reactance, inserted in series with the transmission line to adjust line impedance and thereby control power flow to increase the network security as shown in Fig.1 [13]. | ||||||||||||||||||
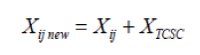 (1) (1) |
||||||||||||||||||
| reactance after the location of TCSC | ||||||||||||||||||
| reactance of the transmission line | ||||||||||||||||||
| reactance of the TCSC | ||||||||||||||||||
| B. Modeling of SVC | ||||||||||||||||||
| SVC is modelled as shunt connected static VAR generator or absorber, QSVC whose output is adjusted to exchange capacitive or inductive compensation and is inserted directly to the load bus as shown in Fig. 2 [14]. | ||||||||||||||||||
| The objective function is to minimize the active power generating cost, which is expressed as: | ||||||||||||||||||
| Where, | ||||||||||||||||||
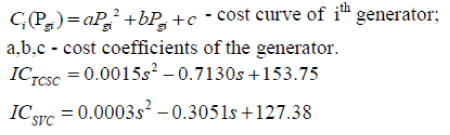 (4) (4) |
||||||||||||||||||
 |
||||||||||||||||||
COMPUTATIONAL INTELLIGENT TECHNIQUES |
||||||||||||||||||
| A. Min cut algorithm | ||||||||||||||||||
| Mechthild Stoer and Frank Wagner presented an algorithm for finding the minimum cut of an undirected edgeweighted graph. It is simple in every respect. It has a short and compact description, is easy to implement, and has a surprisingly simple proof of correctness. Its runtime matches that of the fastest algorithm known. The runtime analysis is straightforward. Min cut algorithm is remarkably simple deterministic with the fastest running time. It reduces the complexity of the algorithm of by avoiding the unnecessary simulated decomposition of the edge set. This enables us to give a comparably straightforward proof of correctness avoiding, for example, the distinction between the unweighted, integer-, rational-, and real-weighted case. This algorithm generalizes our simple approach to the minimization of sub modular functions [15]. | ||||||||||||||||||
| Implementation of Min Cut algorithm involves the following steps: | ||||||||||||||||||
| 1. Find any path from the origin node to the destination node. If there is no more such path, exit. | ||||||||||||||||||
| 2. Determine f, the maximum flow along this path, which will be equal to the smallest flow capacity on any arc in the path (the bottleneck arc). | ||||||||||||||||||
| 3. Subtract f from the remaining flow capacity according to the direction from the origin node to the destination node for each arc in the path. | ||||||||||||||||||
| 4. Go to Step 1. | ||||||||||||||||||
| On termination, the sum of the flows along the paths found during step1 gives maximum total flow between the origin and destination nodes. | ||||||||||||||||||
| The proposed work has two step approach first, the optimal location of the FACTS device in the network must be ascertained by Min Cut and DE algorithms and then, the SCOPF with FACTS devices under normal and contingency operating condition is solved. | ||||||||||||||||||
| B. Differential Evolution Algorithm | ||||||||||||||||||
| Storn presented classical DE algorithm in 1997 which consists of four steps namely initialization of population, mutation, crossover or recombination and selection. | ||||||||||||||||||
| 1) Initialization | ||||||||||||||||||
| DE searches for global optimum point in a D-dimensional real parameter space. The population members are randomly initialized using Equation (14). | ||||||||||||||||||
| where Np - population size; D – dimension; Xi,j (0) - initially generated target vector rand [0,1] - uniformly distributed random number between 0 and 1; i - number of population; j - number of variables; Xjmax - maximum value of the individual; Xjmax - minimum value of the individual. Considering the variables that should be optimized (i.e., the location and the parameter setting of FACTS device). These parameters are randomly initialized within feasible ranges. | ||||||||||||||||||
| 2) Mutation | ||||||||||||||||||
| Mutation is a change or perturbation with a random element. The difference of any two of these three vectors is scaled by a scaling factor F and the scaled difference is added to the third one to obtain the donor vector using Equation (15). | ||||||||||||||||||
| 3) Crossover | ||||||||||||||||||
| To enhance the potential diversity of population, a crossover operation is performed after generating the donor vector through mutation. The trial vector is determined using Equation (16) | ||||||||||||||||||
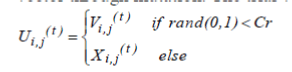 (16) (16) |
||||||||||||||||||
| 4) Selection | ||||||||||||||||||
| The next step is to select target vector or trial vector using the Equation (17) for next generation. | ||||||||||||||||||
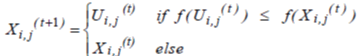 (17) (17) |
||||||||||||||||||
| where f (.) - fitness function | ||||||||||||||||||
| If the trial vector yields an equal or lower value of fitness function, it replaces the corresponding target vector in next generation; otherwise the target vector is retained in the population. Hence, the population gets either better or remains the same in fitness status, but never deteriorates. Stop the process and print the best individual if the stopping criterion is satisfied, else go back to mutation. | ||||||||||||||||||
RESULTS AND DISCUSSION |
||||||||||||||||||
| Differential Evolution algorithm for the optimal location of the TCSC and SVC to obtain secured optimal power flow has been implemented on IEEE 6 bus test system. A. IEEE 6 bus system | ||||||||||||||||||
| There are 11 lines in IEEE 6 bus system. Total system load is 210 MW, the network and load data for IEEE 6 bus system are taken as given in MATPOWER 4.1. | ||||||||||||||||||
| Scenario 1: Under normal operating condition | ||||||||||||||||||
| In order to verify the effects of optimal location of FACTS devices four cases were investigated. | ||||||||||||||||||
| Case 1: OPF without TCSC & without considering line limits | ||||||||||||||||||
| Case 2: OPF without TCSC considering line limits | ||||||||||||||||||
| Case 3: OPF with TCSC considering line limits | ||||||||||||||||||
| Case 4: OPF with SVC considering line limits | ||||||||||||||||||
| From these OPF results shown in Table 1 and Table 2, it is understood that when line limits are not considered the cost is less but 2-4 line gets overloaded. The overload on this line was eliminated by SCOPF solution with considering line limits consequently fuel cost is increased from 3126.36($/hr) to 3143.97($/hr) as shown in Table 1. Placement of FACTS devices at optimal location reduces the flows of heavily loaded lines and maintains the minimum cost of active power generation. | ||||||||||||||||||
| From Table 3, it is understood that the line 1-4 and 2-6 are neighbourhood lines of the over loaded line 2-4. Among these two lines 1-4 is the best location of placing TCSC since it gives minimum cost of active power generation as shown from the results of Min Cut algorithm. The loading of the line 2-4 has now reduce | ||||||||||||||||||
| From Table 4, it is understood that when DE algorithm is applied to obtain the optimal location, the result obtained is line 2(1-4) which is the optimal location of placing TCSC. In addition to that parameter setting of TCSC has found by the DE algorithm and minimum cost of active power generation has obtained. It shows that effectiveness of DE such as less computation time and minimum active power generating cost by the placement of TCSC at optimal location and its parameter setting. Optimal location of SVC and Parameter setting of SVC has found by the proposed method. By placing SVC at optimal location (bus 5) the active power generating cost has further reduced from 3115.84($/hr) to 3102.08($/hr). | ||||||||||||||||||
| From Table 5 it is understood that while placing TCSC at line 2(1-4) with the parameter setting obtained, the loading of the line 2-4 has now reduced to 98.23% from 99.03%.while placing SVC in bus 5 the loading of line 2-4 has further reduced to 84.48%. DE algorithm has found optimal location directly from the computation as shown in Table 6. However the number of branches which need to be investigated to determine the location of TCSC has reduced from 3 branches to single branch. | ||||||||||||||||||
| From Fig.3 and Fig.4, it is understood that in both the cases DE convergences faster with optimal value of objective function. | ||||||||||||||||||
| Scenario 2: Under contingency operating condition | ||||||||||||||||||
| In a power system, if a line is faulted, its power flow will be shared among other lines of the system. This will lead to possible overloading of some of the lines. Among 11 lines in IEEE 6 bus System, three lines are more important lines that have larger effect on remaining system. The effect of outage of each of these three lines on remaining of the system was investigated. If there is congestion in the network, then installation of TCSC, SVC takes place in such a way that the OPF solution obtained without any overloads. From Table 6, it is understood that line 2-4 is getting overloaded in most of the cases. The secured OPF solution while placing TCSC, SVC was listed in Tables 7 to 9.Over load in line 2-4 is eliminated with the installation of TCSC, which is given in Table 8. In Table 7 and Table 9 optimal generation profile for DE algorithm with TCSC and SVC is given. | ||||||||||||||||||
CONCLUSION |
||||||||||||||||||
| Installation of TCSC and SVC devices in a power system improves the system security under normal and contingency operating conditions. The effectiveness of TCSC and SVC devices greatly depends on where the devices are located. In this paper one of the efficient computational intelligence techniques, DE has been successfully used to the problem under consideration. Minimization of active power generation cost is considered as optimization criterion. The proposed method finds the most suitable locations to install TCSC and SVC for reducing the over loading of lines during normal and contingency operating conditions. The simulation is carried out on IEEE 6 bus test system validates the effectiveness of this work. Simulation results show that using TCSC and SVC in the optimal location with the optimal parameter setting can significantly improve the security power systems under single line contingencies. | ||||||||||||||||||
Tables at a glance |
||||||||||||||||||
|
||||||||||||||||||
Figures at a glance |
||||||||||||||||||
|
||||||||||||||||||
References |
||||||||||||||||||
|