COMPARISON OF NONLINEAR MEDIAN FILTERS: SMF USING BDND AND MDBUTM

Sakhare V. C.; V. Jayashree

COMPARISON OF NONLINEAR MEDIAN FILTERS: SMF USING BDND AND MDBUTM

Sakhare V. C.¹, V. Jayashree²

Assistant Professor, Department of Textiles, Textile and Engineering Institute, Ichalkaranji, Maharashtra, India
Associate Professor, Department of Electronics & Telecommunication,Textile and Engineering Institute, Ichalkaranji, Maharashtra, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Digital images are often corrupted by impulse noise which has two models namely, random valued impulse noise and salt & pepper noise. In this paper performance of two modified median filters viz., Switching Median Filter (SMF) using Boundary Discriminative Noise Detection (BDND) algorithm and Modified Decision Based Unsymmetric Trimmed Median (MDBUTM) filter for the removal of impulse noise was tested & compared using Peak Signal to Noise Ratio (PSNR), Image Enhancement Factor (IEF), number of Correctly Detected Corrupted (CDC) pixels, Miss Detected (MD) pixels, False Alarm (FA) pixels and execution time. These two filters basically identify corrupted pixels from noisy image and then filter only those corrupted pixels. In SMF, BDND algorithm is used to determine two boundaries to identify corrupted pixels, and then modified adaptive filter is used to replace corrupted pixels. MDBUTM filter deems pixels having values ‘0’ or ‘255’ as corrupted and replaces these pixels either by trimmed median or by mean of neighborhood pixels. The performance of filters is tested on gray scale images corrupted with variable percentage of salt & pepper noise and random valued impulse noise. Qualitative and quantitative result analysis show that for salt and pepper noise performance of MDBUTM filter and SMF using BDND was found to be nearly equal at all noise densities. For random valued impulse noise, performance of SMF using BDND was found to be better than that of MDBUTM filter. However SMF using BDND requires more time for execution due BDND algorithm.

Keywords

Impulse noise, MF, SMF, MDBUTM, BDND, IEF.

I. INTRODUCTION

Images are often corrupted by the impulse noise. Impulse noise is caused by malfunctioning pixels in camera sensors, faulty memory locations in hardware (faults in data acquisition system) and transmission in a noisy channel [1]. It could severely degrade the image quality and cause some loss of information. So it is important to filter such noise in images before some subsequent image processing such as edge detection, image segmentation and object recognition in the image

There are two models of impulse noise, namely, random valued impulse noise and salt and pepper noise. Random valued impulse noise produces impulse (noisy or corrupted pixel) whose gray level lies within a predetermined range. For example, if gray level exceeds a value LMAX, it is positive or high intensity impulse (LMAX to 255); if gray level is less than LMIN, it is a negative or low intensity impulse (LMIN to 0). For images corrupted with salt and pepper noise, the impulse can take only maximum (255) and minimum (0) values in the dynamic range. The objective of filtering is to remove the impulses so that the noise free image is fully recovered with minimum signal distortion.

Though noise removal can be achieved by using a number of existing filtering techniques but the linear filtering techniques are not effective in removing impulse noise. This has lead to use nonlinear filtering techniques such as median filter [2]. Standard median filter is a robust nonlinear filter which works in the rectangular window area. This filter replaces center pixel of the current window with the median of pixels of the current window. However, this median filtering approach is applied to each pixel unconditionally, that is, without considering whether it is uncorrupted or corrupted. As a result, the image details contributed from the uncorrupted pixels are also subjected to the unnecessary filtering which causes image quality degradation. The disadvantage of this filter is that it is effective only at low noise densities. An intuitive solution to overcome this problem is to implement an impulse-noise detection mechanism prior to filtering such that only those pixels identified as “corrupted” would undergo the filtering process, while those identified as “uncorrupted” would remain intact. Such numbers of variants of nonlinear median filters incorporating different noise detection and filtering schemes are proposed by various researchers. These variants of median filter can be classified in three groups namely Adaptive Median Filter (AMF), Switching Median Filter and Decision Based Median Filter (DBMF). The rest of paper is structured as follows. Section II takes review of AMF, SMFs and DBMFs. Section III provides theoretical background for SMF using BDND and MDBUTM filter which are compared in this paper. Section IV describes experimental procedure. Results are presented in section V and finally conclusion is drawn in section VI.

II. RELATED WORK

AMF works in rectangular window area. It replaces only noisy pixels by median of the window. Ranked order based adaptive median filter (RAMF) detects noisy pixel by using minimum, maximum &median of intensity values from the neighborhood window and maximum filtering window size[3].The performance of RAMF is better than that of median filters at lower noise density levels. However, at higher noise densities, the edges are smeared significantly because large numbers of pixels are replaced by median values which are less correlated with actual pixel value [4].

SMF determines a threshold level to identify corrupted pixels. As the threshold value affects the performance of impulse detection, it is necessary to derive an optimal threshold. Progressive Switching Median Filter (SMF) presented in [5] applies impulse detection and noise filtering stage progressively through several iterations. It compares difference of current pixel and median of filtering window with a threshold. The corrupted pixel processed in the current iteration is used to help the process of the other pixels in subsequent iterations. Another SMF based on an optimal thresholding method [6] compares minimum absolute value of convolution obtained by convolving input noisy image with a set of convolution kernels is compared with a threshold for impulse detection and then only noisy pixels are filtered.

These two filters have two drawbacks. Firstly, the algorithms make use of a fixed noise-detection threshold obtained at a pre-assumed noise density level and hence lack of adaptivity to noise density variation. The mismatch between the designed algorithms and the actual noise density, which is often unknown in priori, will cause noticeable and even substantial degradation on filtering performance. Secondly, when the noise density increases, more misclassifications of pixel characteristic are going to occur and subsequently result in moredegraded filtering performance. Noise Adaptive Soft-switching Median (NASM) filterovercome these two drawbacks and it consists of two stages [7]. A softswitching noise-detection scheme is developed to classify each pixel to be uncorrupted pixel, isolated impulse noise, nonisolated impulse noise or image object’s edge pixel. Then isolated impulses are filtered by standard median filter while edge pixels are filtered by fuzzy weighted median filter. It has been found that above 50% noise density, visual quality of filtered output obtained from NASM significantly degrades due to large number of miss detected pixels.

Number of misclassified pixels is significantly reduced in Switching Median Filter (SMF) with Boundary Discriminative Noise Detection (BDND) [8]. The proposed method uses BDND algorithm to detect noisy pixels and to prepare a binary decision map. From binary decision map noise density is estimated to select maximum window size. Finally only corrupted pixels are processed by noise adaptive filter. It has been shown that performance of this filter is better than other filters.

DBMF deems pixels having minimum and maximum values (for 8 bit image, pixels having 0 and 255 values) as corrupted. Fast and efficient decision based algorithm [4] replaces corrupted pixel by median of neighborhood window. If median value happens to be 0 or 255, it is replaced by previously processed adjacent pixel value. This filter cannot recover edges at high noise level. This drawback is overcome by Decision Based Unsymmetric Trimmed Median (DBUTM) filter [2]. It replaces corrupted pixel by median of 3 * 3 neighborhood window after trimming impulse values from neighborhood window. However at high noise density, if all neighborhood pixels happen to be impulses, trimmed median cannot be obtained. So DBUTM filter does not give better results at high noise density. Modified Decision Based Unsymmetric Trimmed Median (MDBUTM) filter [9] overcomes drawback of DBUTM filter by replacing corrupted pixel by mean of neighborhood window if all neighborhood pixels are 0 and/ or 255 otherwise by trimmed median. Performance of MDBUTM filter is found to be better than DBUTM and DBA.

Since performance of SMF using BDND and MDBUTM filter is better than other filters, these two filters are implemented in this paper. Performance evaluation of these two filters is carried out using Peak Signal to Noise Ratio (PSNR) and Image Enhancement Factor (IEF). It is found that for salt and pepper noise, performance of MDBUTM is nearly equal to that of SMF using BDND at all noise levels. For random valued impulse noise SMF using BDND outperforms MDBUTM filter. The rest of paper is structured as follows. Section II provides theoretical background for SMF using BDND and MDBUTM filter. Section III describes experimental procedure. Results are presented in section IV and finally conclusion is drawn in section V.

III. THEORETICAL BACKGROUND

In this section theory related to impulse noise detection and filtering scheme of SMF using BDND and MDBUTM filter is presented.

A. Switching Median Filter using Boundary Discriminative Noise Detection

In switching median filters the decision of corrupted image pixel is based on a predefined threshold value. The SMF using BDND has three steps viz., noise detection & decision map forming, noise density estimation & maximum window size selection and noise adaptive filtering.

1) Noise Detection and Decision Map formation:The BDND algorithm is applied to each pixel of the noisy image in order to identify whether it is “uncorrupted” or “corrupted” and simultaneously a two-dimensional binary decision map is formed where in ‘0’ is assigned for uncorrupted pixels, and ‘1’ for corrupted pixels.

To accomplish this objective, all the pixels within a pre-defined window that center on the considered pixel will be grouped into three clusters namely low intensity cluster CILow, medium intensity cluster CIMed and high intensity cluster CIHigh. Hence two boundaries b1 and b2 are required for forming three clusters. For each pixel xi,j being considered, cluster assigned is as follows

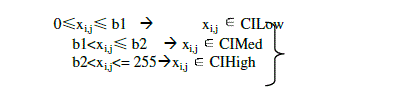If the center pixel being considered falls onto the middle cluster, it will be treated as “uncorrupted”. Otherwise, it is very likely that the pixel has been corrupted by impulse noise.

The boundary discriminative process mainly consists of two iterations. In the first iteration, an enlarged local window with a size of 21*21 (empirically determined) is used to examine whether the considered pixel is an uncorrupted one. If the pixel is deemed as “corrupted” in first iteration, then only second iteration will be invoked to further examine the pixel based on a more confined local statistics by using a 3*3 Window. The steps for boundary discrimination and noise detection of the proposed BDND algorithm are as follows:

1. Take a 21*21 neighborhood in original noisy image centered on the current pixel.

2. Sort the pixels in the window according to the ascending order and find the median, med, of the sorted vector Vo.

3. Compute the intensity difference between each pair of adjacent pixels across the sorted vector Vo and obtain the difference vector VD.

4. For the pixel intensities between 0 and med in the Vo, find the maximum intensity difference in the VD of the same range and mark its corresponding pixel in the Vo as the boundary b1.

5. Likewise, the boundary b2 is identified for pixel intensities between med and 255.

6. Three clusters of pixels are formed using boundaries b1 & b2 and the condition given in eqn. (1).

7. If the pixel belongs to the middle cluster, it is classified as “uncorrupted” pixel, and the classification process stops; otherwise, the second iteration will be invoked as per the following steps

8. Take a 3*3 neighborhood, of the pixel under consideration and repeat Steps 2)–5).

9. If the pixel under consideration belongs to the middle cluster, it is classified as “uncorrupted” pixel, otherwise, classified as “corrupted.”

2) Noise Density Estimation and maximum window size selection:The noise-density, p can be estimated in the BDND by counting the number of 1s on the binary decision map obtained in the impulse-noise detection stage. For modified adaptive filtering, (empirically determined) maximum window size WD1 * WD1 of 3*3, 5 * 5 and 7 * 7 is selected depending upon the noise density range of 0 to 20%, 20% to 40% and above 40% respectively.

3) Noise adaptive filtering algorithm:Based on the binary decision map, “corrupted” pixels are filtered as stated further. First, decision of appropriate neighborhood for filtering is done as follows. Starting with neighborhood of size WF*WF=3*3, if either the total number of uncorrupted pixels obtained from neighborhood is less than half of the total number of pixels or the number of uncorrupted pixels in that neighborhood is equal to zero then the filtering is done by taking next odd neighborhood window size provided that WF ≤ WD1. The current pixel is already deemed as “corrupted”, so it is excluded from the process of filtering. Thus the corrupted pixel is replaced by median of uncorrupted pixels from that window.

B. Modified Decision Based Unsymmetric Trimmed Median (MDBUTM)Filter

MDBUTM filter has two steps viz. noise detection and trimmed median filtering.

1) Noise Detection:In decision based filters, the pixel is deemed as corrupted only if its value is either ‘0’ or ‘255’.

2) Trimmed Median Filtering:In MDBUTM filter, filtering window of size 3*3 is used to filter all corrupted pixels. If all neighborhood pixels of current pixel are 0’s or 255’s or both then current pixels is replaced by mean of the filtering window otherwise 0’s and 255’s are trimmed or removed from neighborhood pixels and current pixel is replaced by median of remaining neighborhood pixels (trimmed median).

C. Performance Measures

The filter performance is quantitatively measured by the Peak Signal to Noise Ratio (PSNR) and Image Enhancement Factor (IEF) as defined in (2) and (4)

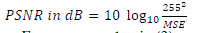Execution time of both the filters is also measured as another performance measure.

Since noise detection plays key role in filtering process, performance of filter is also evaluated in terms of the following

CDC- Number of Correctly Detected Corrupted pixels

MD – Number of Miss Detected pixels i.e. corrupted pixels miss classified as uncorrupted and

FA – Number of False Alarms i.e. uncorrupted pixels being miss classified as corrupted.

IV. EXPERIMENTAL PROCEDURE

Data set used for testing the performance of SMF using BDND and MDBUTM filter are standard test images such as Lena, Baboon & Peppers. These filters are implemented in Java [10]. The steps of experimental procedure are as follows

1. Read standard test image.

2. Add salt and pepper noise of varying density.

3. Apply SMF using BDND and MDBUTM filter on corrupted image.

4. Calculate PSNR and IEF from original, corrupted and restored image for both filters.

5. Count number of CDC, MD, FA pixels for both filters.

6. Repeat steps 1 to 5 for random valued impulse noise.

The experiment on the MDBUTM and SMF using BDND algorithm was extended beyond the aspects considered by the previous researchers in the following points

1. MDBUTM algorithm is applied for image corrupted with random valued impulse noise.

2. Time required for filters to filter the noisy image is also measured.

V. EXPERIMENTAL RESULTS

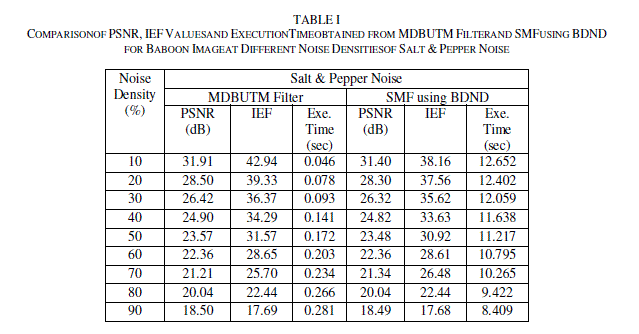
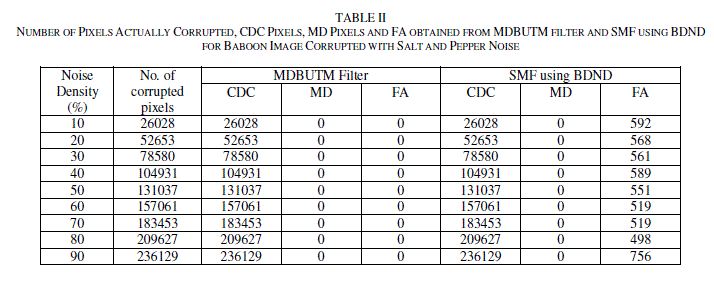
Table I compares PSNR and IEF values obtained for Baboon image by applying SMF using BDND and MDBUTM filter by varying salt & pepper noise density from 10% to 90% respectively. Table II shows number of CDC, MD and FA pixels obtained from MDBUTM filter & SMF using BDND for Baboon image corrupted with salt & pepper noise.

Table III compares PSNR and IEF results obtained for Baboon image by applying SMF using BDND and MDBUTM filter by varying random valued impulse noise density from 10% to 90% respectively. Table IV shows number of CDC, MD and FA pixels obtained from MDBUTM filter and SMF using BDND for Baboon image corrupted with random valued impulse noise.

Based on these results following observations are made

1. For salt and pepper noise, performance of MDBUTM filter and SMF using BDND in terms of PSNR and IEF is nearly equal at all noise densities. However SMF using BDND takes more time for execution due to noise detection and decision map formation stage.

2. Execution time of MDBUTM filter increases with salt & pepper noise density because number of corrupted pixels increases.

3. Execution time of SMF using BDND decreases with salt & pepper noise density because as noise density increases, number of corrupted pixels increases and time required for sorting pixels during BDND algorithm decreases.

4. For salt and pepper noise, MDBUTM filter detects all corrupted pixels correctly thus making miss detected and false alarm pixels zero. It shows that MDBUTM filter, detects salt and pepper noise accurately. (Ref. Table II)

5. In Table II, SMF using BDND is found to detect all corrupted pixels for salt and pepper noise. But though miss detected pixels are zero, there are some false alarms which are not desired.

6. For random valued impulse noise, SMF using BDND outperform MDBUTM filter for all noise levels from 10% to 90%.

7. From Table IV it is seen that for random valued impulse noise, as the MDBUTM filters only pixels having 0 or 255 value, therefore number of correctly detected corrupted pixels is very low that of while miss detected pixels are large. Hence execution time of MDBUTM filter is very low (Ref. Table III). Since large number of pixels are miss detected, performance of MDBUTM filter for random valued impulse noise is poor.

8. As per Table IV for random valued impulse noise, the performance of SMF using BDND is good up to 40% noise density and above 40% noise density performance starts to degrade because of increase in number of miss detected pixels and large decrease in correctly detected corrupted pixels.

9. Filtered images shows that for salt and pepper noise at 80% level, quality of output obtained from MDBUTM filter and SMF using BDND is nearly equal. (Ref. Fig. 1(c) and 1(d))

10. For random value impulse noise, it is found from Fig. 2(c) and 2(d) that quality of output image obtained from SMF using BDND is much better than that of MDBUTM filter. However in the output of SMF using BDND (Fig. 2(d)), some noise is seen because of miss detected and false alarm pixels.

VI. CONCLUSION

In this paper performance of two nonlinear median filters, SMF using BDND and MDBUTM filter is tested and compared on gray scale images for salt & pepper noise and random valued impulse noise. From the qualitative and quantitative result analysis we can conclude that for salt & pepper noise, the performance of MDBUTM filter and SMF using BDND is nearly equal at all noise levels. But when execution time is important then MDBUTM filter is preferable. For random valued impulse noise, though SMF using BDND requires more execution time, noise detection by SMF using BDND is better than that of MDBUTM filter, so also performance is. But performance of SMF using BDND is found to be good up to 40% noise level. Thus further reduction in the execution time and performance improvement above 40% random valued impulse noise is desirable. Also work is to be carried out further for color test images.

References

R. C. Gonzalez and R. E. Woods, Digital image processing, 2nd ed., Pearson Education, India: 2003
K. Aiswarya, V. Jayaraj, and D. Ebenezer, “A new and efficient algorithm for the removal of high density salt and pepper noise in images and videos,” in Second Int. Conf. Computer Modeling and Simulation, 2010, pp. 409–413
H. Hwang and R. A. Haddad, “Adaptive median filter: New algorithms and results,” IEEE Trans. Image Process., vol. 4, no. 4, pp. 499–502, Apr. 1995.
K. S. Srinivasan and D. Ebenezer, “A new fast and efficient decision based algorithm for removal of high density impulse noise,” IEEE Signal Process. Lett., vol. 14, no. 3, pp. 189–192, Mar. 2007
Zhou Wang and David Zhang, “Progressive Switching Median Filter for the Removal of Impulse Noise from Highly Corrupted Images”, IEEETransactions On Circuits And Systems—II: Analog And Digital Signal Processing, vol. 46, no. 1, pp. 78-80, Jan. 1999
S. Zhang and M. A. Karim, “A new impulse detector for switching median filters,” IEEE Signal Process. Lett., vol. 9, no. 11, pp. 360–363, Nov. 2002.
H. L. Eng and K. K. Ma, “Noise adaptive soft-switching median filter”, IEEE Transactions Image Processing, vol. 10, no. 2, pp. 242-251, Feb. 2001
P. E. Ng and K. K. Ma, “A switching median filter with boundary discriminative noise detection for extremely corrupted images,” IEEE Trans. Image Process., vol. 15, no. 6, pp. 1506–1516, Jun. 2006
S. Esakkirajan, T. Veerakumar, Adabala N. Subramanyam, and C. H. PremChand, “Removal of high density salt and pepper noise through modified decision based unsymmetric trimmed median filter”; IEEE Signal Processing Letters, vol. 18, No. 5, pp. 287-290, May 2011
H. Schildt, The Complete Reference Java 2, 5th ed., Tata McGraw Hill, New Delhi, India: 2002