ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Dan Zhou PhD Student, Beijing Key Laboratory of High Voltage & EMC, North China Electric Power University, Beijing, China |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The paper is concerned with transformer Weibull lifetime modelling which is recognised as essential for effective asset management within electric utilities. Two popular and widely adopted methods, maximum likelihood estimation and median rank regression, are discussed and compared for their properties in estimating transformer lifetime data. To greatly mimic the field collected transformer lifetime data, Monte-Carlo simulations are conducted to generate multiple sets of transformer lifetime data with the censoring rate being set at 90% and sample size chosen as ranging from 60 to 1000. Weibull parameters are estimated for each sample set with both methods. Performance of each estimation method is then evaluated with respect to their corresponding relative difference between median value and the true value (RD) as well as the relative root mean square error (RRMSE) obtained for each sample size. It is found that the maximum likelihood method is superior to the median rank regression method due to the fact that it always provides smaller RD as well as RRMSE and is hence recommended to be used for transformer Weibull lifetime modelling.
Keywords |
||||||||
| Maximum likelihood estimation, median rank regression, Monte Carlo simulation, transformer lifetime, Weibull distribution | ||||||||
INTRODUCTION |
||||||||
| Power transformers are generally highly reliable equipment with relative long anticipated lifetimes, e.g. designed life expected to be around 40 years [1]. However, as a large number of transformers installed in the loading growth period of 1960s and 1970s are approaching or have already exceeded their designed lifetime [2-3], concerns are aroused on these large number of aged equipment and their impact on the power network [4]. Although most of the aged transformers in service are still in safe operating condition, their future performances are yet unclear. Replacement of aged transformers before they reach an unacceptable state has to be made in order to avoid unexpected supply loss. Moreover, transformers are capital intensive assets with a long acquisition lead time; currently it takes 15 months or more [5]. Forward replacement planning is therefore required. | ||||||||
| All these drive the demand of effective transformer lifetime modelling, for which the general procedure is to choose an appropriate statistical distribution function and then determine the parameters of the distribution function using collected lifetime data. Statistical distributions are chosen according to their representativeness of equipment’s failure characteristics (or more specifically, the general hazard rate versus age relationship). As specified in [6], early mortalities are not obvious for power transformers nowadays; their hazard rate remains constant over some time and then exhibit an increasing trend as they age. This can be modelled with two-parameter Weibull distribution with different shape parameters. | ||||||||
| To estimate the parameters of the Weibull distribution, various estimation methods have been proposed by different authors [7-10]. Among which, maximum likelihood estimation (MLE) method is the most popular in terms of the theoretical prospective and the median rank regression (MRR) method is computationally easier to handle and provides simple closed form solutions for the estimates. Comparisons between MLE and MRR have been made by some researchers [11-14]. These studies, however, resulted in contradictory opinions on the preference of one method over the other, as they were conducted with different data generating mechanisms at various censoring levels. It is suggested that for application in a specific situation, simulations should be designed to greatly mimic that specific sampling scenario based on which optimal method can be chosen. | ||||||||
| This paper therefore discusses and compares MLE and MRR for their properties in estimating transformer lifetime data. MLE and MRR are briefly summarized in Section II. After analysing the characteristics of field collected transformer lifetime data, Monte Carlo simulations are designed and conducted to simulate multiple sets of transformer lifetime as presented in Section III. Comparisons are then made in terms of the relative difference between the median value and the true value (RD) as well as the relative root mean square error (RRMSE) of the estimates. Results are presented and discussed in Section IV based on which conclusions are finally drawn. | ||||||||
WEIBULL DISTRIBUTION AND PARAMETER ESTIMATION METHODS |
||||||||
| A. The Weibull Distribution Function | ||||||||
| Cumulative distribution function (CDF) of the two-parameter Weibull distribution [9] is presented in (1). It’s corresponding reliability function (RF), probability density function (PDF) and hazard function (HF) are listed in (2)- (4), respectively. | ||||||||
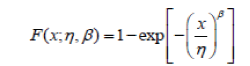 (1) (1) |
||||||||
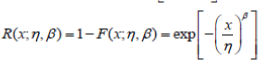 (2) (2) |
||||||||
 (3) (3) |
||||||||
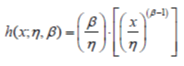 (4) (4) |
||||||||
| where | ||||||||
| x is the failure time, expressed as a variable; | ||||||||
| η is the scale parameter or termed as the characteristic lifetime; | ||||||||
| β is the shape parameter. | ||||||||
| A very important characteristic of the two-parameter Weibull distribution is that the value of the shape parameter corresponds to the three regions of the bathtub curves as follows | ||||||||
| β<1 corresponds to region 1 of the bathtub curve, where hazard rate decreases as transformer ages; | ||||||||
| ïÃâ÷ β=1 corresponds to the region 2 of the bathtub curve, where hazard rate is independent of the time; | ||||||||
| β>1 corresponds to region 3 of the bathtub curve, representing the relationship that hazard rate increases as transformer ages. | ||||||||
| The scale parameter, η, represents the time by which 63.2% of the transformers are expected to have failed. For the special case that β=1, the value of η is the same as the mean lifetime of the distribution. | ||||||||
| B. Maximum Likelihood Estimation | ||||||||
| In present days, transformer lifetime data are often collected as incomplete dataset as a large number of units are still in safe operating condition. Maximum likelihood estimation [11] can be adopted to deal with these two types of data. Suppose that a set of lifetime data is collected from N transformer units as (X1, X2,…, Xr, Cr+1,Cr+2,…, CN), among which the first r units are observed as failure data for whom the event of failure is actually observed, whereas the remaining N-r units are survival data for whom the event of failures are not observed yet but only known to be beyond the current running times. Likelihood function of this dataset is as follows: | ||||||||
| Insert RF and PDF of Weibull distribution as shown in (2) and (3) into (5) and then taking the natural logarithm, the equation is then transformed as: | ||||||||
| Taking partial derivative oflnL(η, β) with respect to η and β respectively, and setting the corresponding value as zero, we have: | ||||||||
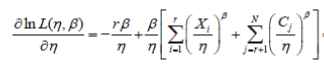 =0 (7) =0 (7) |
||||||||
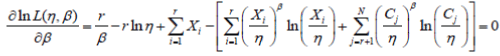 (8) (8) |
||||||||
| By transforming (7) and (8), the estimates of Weibull parameters are found to be solutions of (9) and (10). | ||||||||
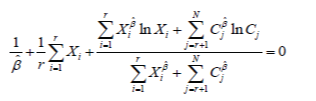 (9) (9) |
||||||||
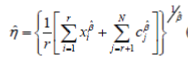 (10) (10) |
||||||||
| ˆÃ¯ÃÂâ can be solved with numerical methods, such as the Newton-Raphson method [15]. Once ˆÃ¯ÃÂâ is determined, ïÃÂèˆ can be obtained by taking ˆÃ¯ÃÂâ into (10). | ||||||||
| C. Median Rank Regression | ||||||||
| To estimate the Weibull parameters, median rank regression [11] linearizes the Weibull data and then performs simple linear regression on the transformed data. The basis is the transformation of Weibull CDF; the transformed equation is as shown in (11). | ||||||||
| Denoting ln(-ln(1-F(x;η,β))) as y, equation (11) becomes a linear model between y and lnx. In this respect, the parameters, i.e. η and β, can be estimated with the least squares procedure as long as the point pairs (lnx, y) are determined. Let Li be the ith ordered failure and Yi be the estimate of F(Li). Then the least square equations are | ||||||||
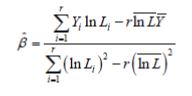 (12) (12) |
||||||||
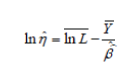 (13) (13) |
||||||||
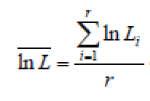 (14) (14) |
||||||||
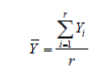 (15) (15) |
||||||||
| For a complete dataset, the CDF F(Li) hence Yi is directly estimated as | ||||||||
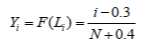 (16) (16) |
||||||||
| where N is the total number of the collected lifetime data. For an incomplete dataset which is the case for the present study, the rank value, i, in (16) is replaced by the adjusted rank defined as: | ||||||||
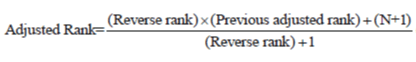 (17) (17) |
||||||||
DESCRIPTION OF THE SIMULATION |
||||||||
| A. Design of the Simulation | ||||||||
| Assume that the failure times of a transformer fleet follow a Weibull distribution with parameters (ηT, βT), termed as true values of the distribution. For the ith unit in the transformer fleet, its failure time, Xi(1 ≤i≤N), can be randomly sampled from the inverse of the Weibull CDF, as: | ||||||||
| whereUi is a random number. | ||||||||
| whereUi is a random number. The collected lifetime data, Li, for this specific unit is then specified after comparing its failure time, Xi, with a fixed censoring time, TC, which is actually the time duration of the observation. The value of Li is determined as: | ||||||||
| Equation (19) represents the time censoring process that if Xi<TC, the unit failed at timeXi, whereas ifXi≥TC, the unit is censored. | ||||||||
| Repeat the above procedure for N times, a lifetime dataset for a transformer fleet containing N units can be simulated. Besides the sample size, N, another important term that helps to characterise the lifetime dataset is the censoring rate, CR, defined as the proportion of units being censored. By controlling the censoring time, lifetime datasets of transformer fleets with desired CR can be sampled.To greatly mimic the field collected transformer lifetime data, controlling parameters for the simulation are chosen as listed in Table I. | ||||||||
| The two pairs of scale and shape parameter are chosen as (500, 1), (100, 5) to reflect utility’s current understanding on the distribution of random and ageing-related failures respectively. Sample sizes are chosen to cover a wide range from 60 to 1000. The censoring rate, CR, is chosen as 90% to reflect the current situation of field collected transformer lifetime data that the censoring rate are normally in the high value range, mostly over 80% [16-19]. | ||||||||
| B. Criteria for the Comparison | ||||||||
| To assess the performance of MLE and MRR, the relative difference between median value and the true value (RD) the relative root mean square error (RRMSE), as defined in (20) and (21), for each method were calculated using 10000 replications of lifetime data for each of the cross-combinations of the controlling parameter levels. | ||||||||
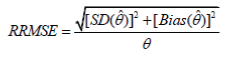 (21) (21) |
||||||||
| where | ||||||||
| θ is the true value of the parameter; | ||||||||
| is the estimated value of the parameter; | ||||||||
| SD(ïÃÂñˆ) is the standard deviation of the estimated parameters. | ||||||||
| RD is chosen to reflect the central tendency of the results, whereas the RRMSE is adopted for the purpose for an overall evaluation of the results. The two metrics hence complement each other for an effective evaluation. It is expected that the closer the RD and the RRMSE to zero, the higher the accuracy level of the estimated parameters will be. Consequently, properties of different parameter estimation methods in estimating the same sets of lifetime data can be compared. | ||||||||
RESULTS AND DISCUSSIONS |
||||||||
| A. Results of Shape Parameter β | ||||||||
| RD and RRMSE of the estimated βs obtained by MLE and MRR are presented together in Fig. 1 and Fig. 2, respectively. Results obtained by MLE are plotted as yellow bars, whereas results obtained by MRR are presented as magenta bars. Results obtained while βT=1 and βT=5 are presented in bars filled with different patterns for differentiation. This format is maintained throughout this paper. | ||||||||
| As shown in Fig. 1 and Fig. 2, observations made are: | ||||||||
| 1) RD and RRMSE obtained by MLE are always smaller and hence closer to zero than results obtained by MRR in the same scenario. This indicates that MLE can provide more accurate result in estimating β compared with MRR. | ||||||||
| 2) RDs obtained by MLE are always in the positive value range, whereas RDs obtained by MRR are always in the negative value range. This implies that β tends to be overestimated by MLE whereas underestimated by MRR. | ||||||||
| 3) The influences of sample size are observed. RDs and RRMSEs are moving closer to zero as the sample size increases which indicate that the accuracy of estimated β is improved as the sample size increases. This correlates well with the law of large numbers in probability theory. | ||||||||
| 4) The influence of true β value is not observed in estimating β, the same accuracy level of estimated β is hence maintained throughout different βT. No difference of RD between the case of βT=1 and βT=5 is observed for both MLE and MRR, as shown in Fig. 1. So is the RRMSE, as shown in Fig. 2. | ||||||||
CONCLUSION |
||||||||
| Two popular Weibull parameter estimation methods, maximum likelihood estimation (MLE) method and median rank regression (MRR)method are evaluated and compared in terms of their properties to deal with transformer lifetime data. Extensive Monte Carlo simulations were conducted so that corresponding evaluation metrics, the relative difference between the median value and true value (RD) as well as the relative root mean square error (RRMSE) for the two methods are obtained. Results show that the shape parameter of the Weibull distribution tends to be overestimated with MLE but underestimated with MRR. The scale parameter of the Weibull distribution tends to be underestimated with both methods. Overall comparison show that MLE is superior to MRR as it always provides lower RD and RRMSE for both estimated shape parameters and scale parameters. MLE is hence recommended to be adopted over MRR for transformer Weibull lifetime modelling. | ||||||||
ACKNOWLEDGMENT |
||||||||
| The author would like to express her appreciation to the China Ministry of Science and Technology for supporting this research under National Key Basic Research Program (973 Program) under the contract number 2009CB724508. | ||||||||
Tables at a glance |
||||||||
|
||||||||
Figures at a glance |
||||||||
|
||||||||
References |
||||||||
|