International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Computing the Determinants in the Multiprocessor Computer

Salman H. Abbas
Associate Professor, Department of Mathematics, College of Science, University of Bahrain, Kingdom of Bahrain
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper presents a new parallel algorithm for computing the determinants of block matrices of order 𝑤 × Ã°ÂÂ‘Â¤, with Computational Complexity 𝑂 𝑤 3𝑞2 2 , using the Gauss elimination method and Abbas's block method 7 as references. We present our algorithm using Ada-multitasking. The algorithm is numerically stable and has been tested in the Sequent Balance machine with efficient utilization of all processors

KEYWORDS
Determinants, Gauss elimination method, Multitasking, Theoretical and experimental costs.

I.INTRODUCTION
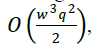image
The time spent on inter-processor communication will be dominant constraint on the performance of optimal algorithm when the matrix and multiprocessor sizes are Large. Some authors have discussed the effect of the communication network of multiprocessor on the communication costs incurred when using a multiprocessor 1 , 2 , 3 ,and the effect of the Communication costs on the execution time of parallel algorithm 4 , 5 . The outline of this paper is as follows: we describe our algorithm and problem assumptions in Section 2. In Section 3, we describe the parallel algorithm. In Section 4,we give the total costs of the sequential and parallel algorithms. We briefly summarize the results and make Concluding remarks in Section 5.

II. RELATED WORK
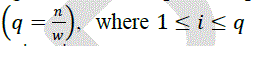imageimplementationCan be used to improve the efficiency in terms of the speedup and the number of processors. It is mentioned in [13]The total cost for computing the determinant is bounded by O(m2) arithmetic operations ,where m is the size of the determinant which is exactly similar to our algorithm. Finally in [14] , a new method was developed to calculate every determinant of size nxn (when n>2),by calculating four determinants of size (n-1)x(n-1) and one determinant of size (n-2)x(n-2) on condition that (n-2)x(n-2) to be different than zero.It is reported that the time complexity of this method is O(n).

ALGORITHM
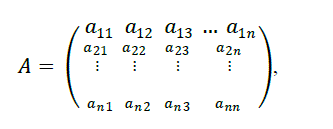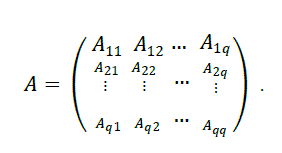image
image

III. PARALLEL ALGORITHM
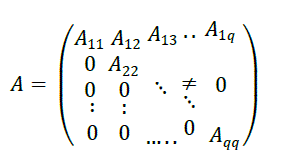image

A) SEQUENTIAL ALGORITHM COST
In the sequential mode the cost depends only on the number of arithmetic operations required for the algorithm. So, reducing the blocks below the diagonal to zeros requires:
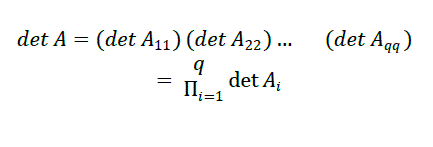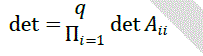image

IV. PARALLEL ALGORITHM COST
Here,we give the predicted cost of the algorithm mentioned in the previous section 3 in terms of arithmetic operation count, communication cost and data sending. A test program was written to measure these quantities. The estimate of the cost of one arithmetic operation, ��ƒ, is0.26 millisec, the time to set up one rendezvous, ���� , is 2 millisec and the time to send one data item,���� ,is 0.02 millisec.
The following table describes the number of multiplication and additions and the number of steps required for each operation. It is assumed that there are at least �� processors.
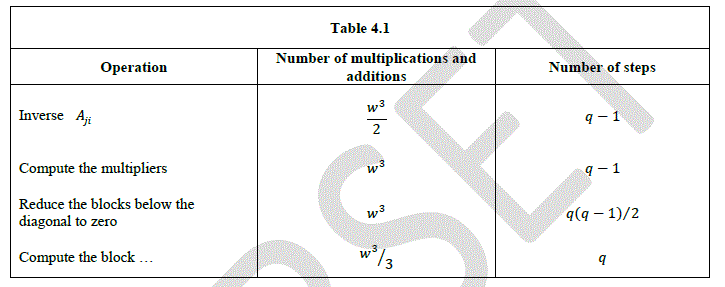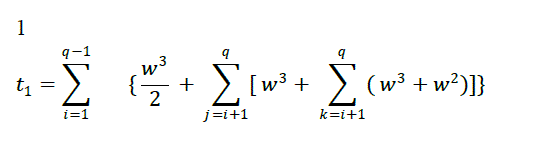image
image

COMPUTATIONAL RESULTS
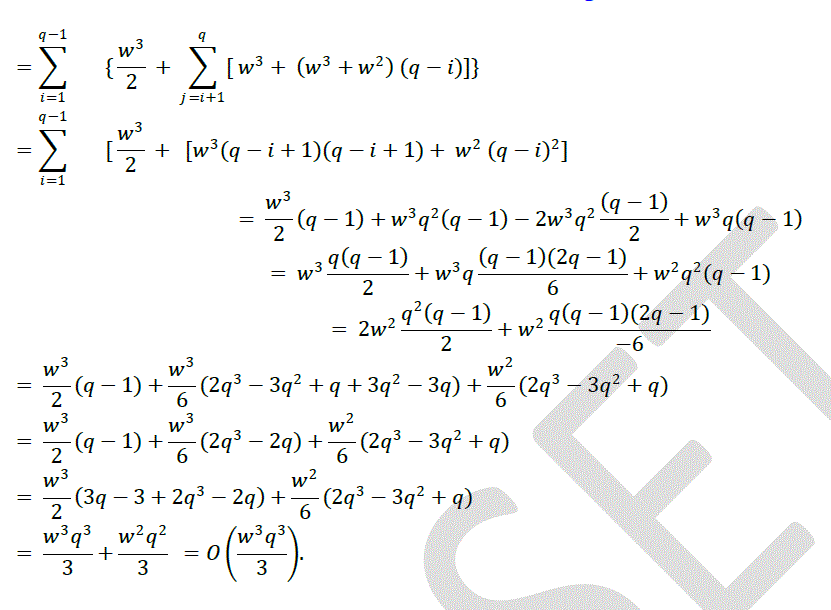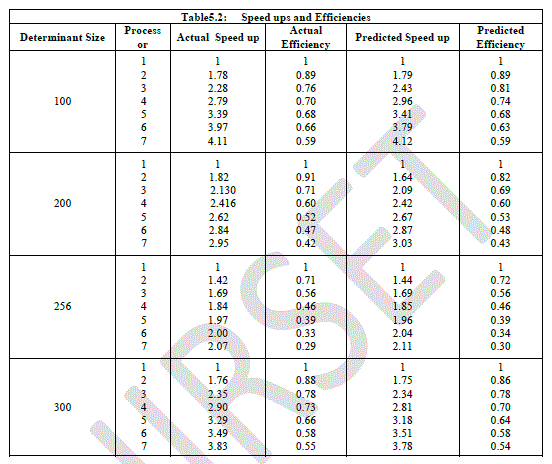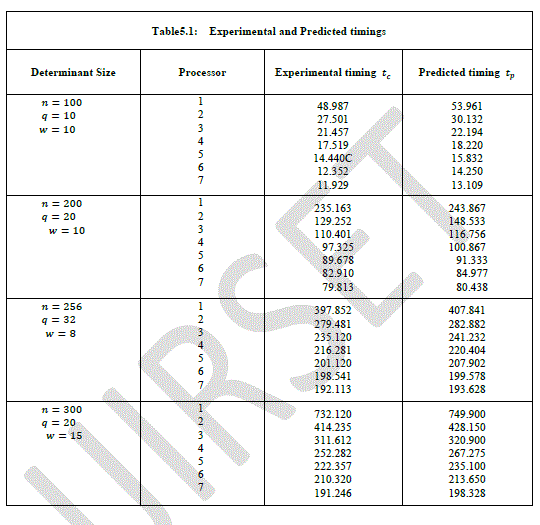
image
image
image
From the above tables we have seen that several runs for different sized determinant is made. Table 5.1 is presented the predicted timings which was calculated from the formula (3) and the corresponding the experimental timings. It is noteworthy to point out that performance improves with increasing the number of processors. In table 5. 2, we give the predicted speed up and efficiency and corresponding for the experimental.
We observe that our theoretical estimate of the speed up and efficiency predicts accurately the performance of the algorithm. This occurs because the sizes of the determinants are very large. In practice if the size of the determinants have the same number of processors we might have a poor speed up and efficiency [10].

V. CONCLUSION
In this paper we have developed a parallel algorithm for computing the determinants in the multiprocessor computer. The advantages of the algorithm are ease of implementation and good suitability for parallel computing. It is designed to handle large determinants whose storage requirements cannot fit on a single computer. Also we can conclude that our proposed algorithm reaches good efficiency even with increasing of the number of processors.

VI. ACKNOWLEDGMENTS
The author is grateful for financial support from the University of Bahrain, the project No. 2012/55.

References
  1. Cvetanovic,Z,"The Effect of Problem Partitioning Allocation and Granularity on the Performance of Multiprocessor System", IEEE Trans. Computers, vol. C-36, pp. 42-432, 1987.
  2. Gannon,D. B. and Van Rosendale,J, “On the Impact of the Communication Complexity on Design of Parallel Numerical Algorithm, " IEEE Trans. Computers, vol. C-33, pp. 1180-1194, 1984.
  3. Lundsrom,S. L, "Application Consideration in the System Design of Highly Concurrent Multiprocessors", IEEE Trans. Computers, vol. C-36, pp. 1292-1309, 1987.
  4. Greiner,J. and Blelloch,G. E, "Connected Components Algorithms”. In Sabot,G.W, editor, High Performance Computing: Problem Solving with Parallel and Vector Architectures. Addison Wesley, Reading , MA, 1995.
  5. Ladd, S., "Guide to Parallel Programming", Springer – verlag, 2004.
  6. Kopta,D. and Davis,A, "Efficient MIMD Architectures for High – Performance Ray Tracing", Int. Rep., University of Utah, School of Computing, 2009.
  7. Abbas,Salman H.,"Complexity of Parallel Block Gauss Jordan Algorithm", Journal of Association of Arab Universities for Basic and Applied Science, vol. 7, pp.57-65, 2009.
  8. Abbas,Salman H.,"On the Cost of Sequential and Parallel Algorithm for Solving Linear System of equations", Int. J. of Computer Mathematics, vol. 74, Issue 3, pp.391-403,2000.
  9. Abbas,Salman H.,"Parallel Solution of Linear System of Equations using a Column Oriented Approach", Chaos, Soliton& Fractals, vol. 30, Issue 4, pp. 864-874, 2006.
  10. Abbas,Salman H.,"Parallel solution of Linear System of Equations on Transputer Array", Applied Mathematics & Information Sciences vol. 2, No. 2, pp. 225-235, 2008.
  11. Beliakov,G. and Matiyasevich,Y.,"A Parallel Algorithm for Calculating of Large Determinants with Accuracy for GPUS and MPI Clusters" ariXiv.1308.1536v2,Accessed Augest 2013.
  12. Kamgin,E.,Nguenange,L. and Phillippe,B.,"Some Efficient Methods For Computing the Determinants of Large Sparse Matrices",ARIMA, Volume xx,pp.1-10,2012.
  13. Haque,S and Maze,M.,"Determinant Computation on the GPU using condensation Method", Technical Report,pp.1-10 ,University of western Ontario,London N6A 1MA ,Canda,2012.
  14. Saliha,A.,"A New Method to Calculate the Determinants of nxn Matrix by reducing determinants to second order", International Conference on Applied Analysis and Algebra,YildizTechnocal University ,20-24 June 2012,Istanbul,Turkey.