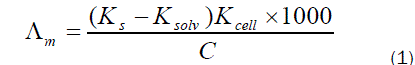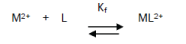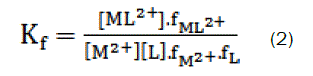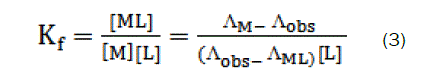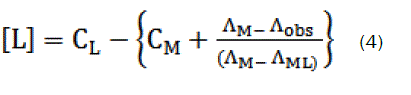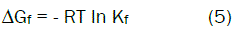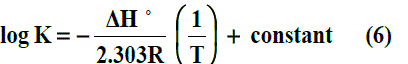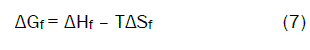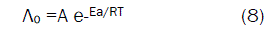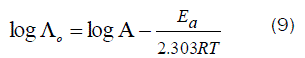Conductance Studies on Complex Formation between CaCl2 and Ampicillin as Ligand in Water and In Methanol Solvent at Different Temperatures

Abstract

The complexation reactions between the metal cation (Ca2+) and ligand (ampicillin) was studied in water and in pure MeOH solvent at 293.15, 298.15, 303.15 and 308.15K by applying the conductometric method. Consequently, we will study the effect of solvent properties on stoichiometry, the selectivity between ligand and ions in various systems and thermodynamic parameters of complexation. On drawing the relation between molar conductance and the ratio of metal to ligand concentrations, different lines are obtained indicating the formation of 1:1, and 2:1 (M:L) stoichiometric complexes. The stability constant of the complexes were obtained from fitting the molar conductivity curves using a computer program. This research focused on the study of thermodynamic complexation reactions between the ligand, ampicillin, with Ca2+ metal cation in water and pure MeOH solvent.

Keywords

Complexation, formation constant, Gibbs free energy, ampicillin, enthalpy and entropy of complexation.

Introduction

The study of the interactions involved in the complexation of different cations with ligand in solvent mixtures is important for a better understanding of the mechanism of biological transport, molecular recognition, and other analytical applications.

Recently, there has been much research on complex formation. There are a number of physico-chemical techniques that can be used in the study of these complexation reactions, for example, spectrophotometry, polarography, NMR spectrometry, calorimetry, potentiometry and conductometry [1]. Nevertheless of all these techniques, conductometric techniques are the most useful for studying this complexation of complexes. This is because conductometric techniques are highly sensitive and inexpensive, with a simple design of experimental arrangement for such investigations [2]. Therefore, it offers more benefits than the other methods

Transition metal ions have a strong role in bio-inorganic chemistry and redox enzyme systems and may provide the basis of models for active sites of biological systems [3]. The chemistry of β-lactam antibiotic is of interest due to their versatile application in medicine and biology. Ampicillin is a penicillin β -lactam antibiotic used in the treatment of bacterial infections caused by susceptible, usually gram-positive organisms. [4]. The pharmacology and clinical efficiency of ampicillin and amoxicillin were extensively studied by many worker [5].

In this study, we discuss the complexation reaction between ampicillin that acts as a ligand with divalent cations in water and in methanol at different temperatures (293.15, 298.15, 303.15 and 308.15K). This study has been conducted at different temperatures by applying the conductometric method. Consequently, we will study the effect of solvent properties on stoichiometry of complexes formation between ligand and ions in various systems.

Experimental

Material and methods

All chemicals used were of the highest purity available and were purchased from Merck.

The ligand

Molecular Structure of Ampicillin sodium salt:

Conductometric titration

In a typical experiment, 10 m; of the ampicillin solution (1.0 x 10-4 M) was placed in the titration cell, thermostated at the preset temperature and the conductance of the solution was measured after the solution reached thermal equilibrium. Then, a known amount of the CaCl₂ solution (1.0 x 10-3 M) was added in a stepwise manner using a calibrated micropipette. The conductance of the solution was measured after each addition until the desired cation-to-ligand mole ratio was achieved. The specific conductance values were recorded using conductivity bridge HANNA, H1 8819N with a cell constant equal to 1. The conductometer was conducted with a thermostat of the type the Kottermann 4130 ultra thermostat. The temperature was adjusted at 293.15, 298.15, 303.15 and 308.15 K.

Result and Discussion

The molar conductance (Λm) values were calculated using equation (1):

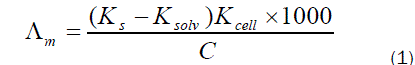
Where K_s and K_solv are the specific conductance of the solution and the solvent, respectively ; K_cell is the cell constant and C is the molar concentration of the CaCl₂ solution.

By drawing the relation between molar conductance (/\m) and the molar ratio of metal to ligand [M]/[L] concentrations different lines are obtained with sharp breaks indicating the formation of 1:1 and 2:1 [M : L] stoichiometric complexes, Fig. (1-4).

Figure 1: The relation between molar conductance ( Λ_m ) and the [M]/[L] molar ratio of CaCl₂ to ampicillin in water at different temperatures.

Figure 2: The relation between molar conductance ( Λ_m ) and the [M]/[L] molar ratio of CaCl₂ to ampicillin in methanol at different temperatures.

Figure 3: The relation between (log K_f) and (1/T) for (1:1) and (1:2) M to L stoichiometric complexes of CaCl₂ and ampicillin in water.

Figure 4: The relation between (log K_f) and (1/T) for (1:1) and (1:2) M to L stoichiometric complexes of CaCl₂ and ampicillin in methanol.

As is obvious from Fig. (1-4), in all cases studied, addition of the CaCl₂ solution to the ligand (ampicillin ) solutions caused a continuous decrease in the molar conductance of the solutions, indicating the lower mobility of the complexed cations compared to the solvated ones. In all cases, the slope of the molar conductance-mole ratio plots change sharply at the point where the ligand to cation mole ratio indicate the formation of stoichiometric complexes, indicating the formation of a relatively stable 1:1 and 2:1 [M : L] complex between the ligand and the cation solutions used.

The 1:1 binding of the Ca²⁺ cations with ampicillin ligand can be expressed by equilibrium:

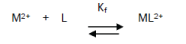
and the corresponding formation constants (K_f) for Ca²⁺-ampicillin complexes were calculated by using equation:

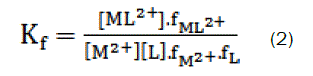
where [ML²⁺],[M²⁺], [L] and f represents the equilibrium molar concentrations of complex, free cation , free ligand and the activity coefficients of the species indicated, respectively.

Under the dilute conditions used, the activity coefficient of the uncharged ligand, fL can be reasonably assumed to as unity [6,7]. The use of Debey-Hückel limiting law of electrolytes [8] leads to the conclusion that & , so that the activity coefficients in Eq. 2 cancel out.

Thus, the complex formation constant in terms of the molar conductance can be expressed as [9-11]:

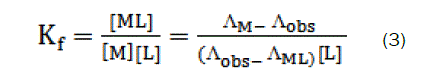
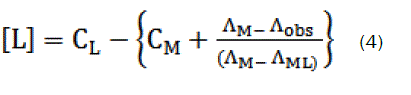
here, ΛM is the molar conductance of the CaCl₂ solution before addition of the ligand, ΛML the molar conductance of the complex, Λobs the molar conductance of the solution during titration, CL the analytical concentration of the ligand, and CM²⁺, the analytical concentration of the CaCl₂ solution. The complex formation constant, K_f, and the molar conductance of the complex, ΛML, were obtained by computer fitting of Eqs. (3) and (4) to the molar conductance- mole ratio data using a nonlinear least- squares [12].

The stability constants of the resulting 1:1 and 2:1 [M:L] complexes were determined from the computer fitting of Eqs. 3 and 4 to the molar conductance-mole ratio data. A sample computer fit of the mole ratio data is shown in Fig. (1-4) and all K_f values are summarized in Table 1.

Table 1: The formation constants (log K_f) of formation of CaCl₂ and ampicillin complexes in water and in methanol at different temperatures.

The Gibbs free energies of formation for each stoichiometric complex were calculated by:

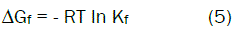
The calculated ΔG_f values are presented in tables (2).

Table 2: The Gibbs free energies (ΔG_f) of formation of CaCl₂ and ampicillin complexes in water and in methanol at different temperatures.

The enthalpy changes of complexation (ΔH_f) were calculated from the plots of log K_f against 1/T, (slope = -ΔH/2.303 R) (Fig. 5) using Van’t Hoff eqn .6:-

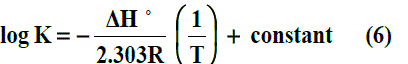
Where R is the gas constant and T is the absolute temperature.

Figure 5: The relation between (log Λo) and (1/T) for (1:1) M to L stoichiometric complexes of CaCl₂ and ampicillin in water.

Entropy change ΔS were for complexes calculatd [13-85] by using Gibbs-Helmholtz equation (6)

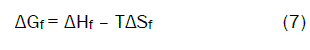
The calculated values of (ΔH_f) and (ΔS_f) for CaCl₂-ampicillin stoichiometric complexes are presented in Table (3)

Table 3: The enthalpies (ΔH_f) and entropies (ΔS_f) of formation of CaCl₂ and ampicillin complexes in water at different temperatures.

In order to obtain a better understanding of the thermodynamics of the complexation reactions, it is useful to consider the enthalpic and entropic contributions to these reactions. The enthalpy and entropy of the complexation reactions were determined by measuring the formation constants as a function of temperature. Enthalpies and entropies of complexation reactions show that, in most cases, the reaction is entropic controlled although, in all cases, a negative value of enthalpic change is also obtained Comparison of ΔH_f values of complexation (Table 3) clearly revealed that the steric hindrance in organic ligand is an important factor in enthalpy changes in the process of complexation reactions. On the other hand, in most cases, the entropy changes during complexation reactions are quite favorable. The entropic change during the complex formation is in fact affected by several factors including the change in flexibility of the reactants in the course of complexation reaction and the differences between the extent of solvation– desolvation of the uncomplexed and complexed species. In the case of the complexation reactions of ligand with Ca²⁺ cations, a large positive ΔS_f was obtained. This observation seems to be due to strong solvation of ligand by solvent alike MeOH [13–32]; during the process of complex formation with the ligand, these solvent molecules are liberated, causing a favorable entropic change. Interestingly to note, a comparison between the ΔS_f, ΔH_f and ΔG_f values reported in Table 2&3 reveals that generally a decrease in ΔH_f value is accompanied with an increase in ΔS_f in such a way that the free energy change ΔG_f will remain more or less constant. Such enthalpy-entropy compensation effect was observed earlier in the case of complexation reactions of ligands with cation and inorganic guest species [33-85].

Since the conductance of an ion depends mainly on its mobility, it is quite reasonable to treat the rate process taking place with the change of temperature on the basis of equation(8):

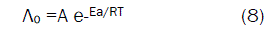
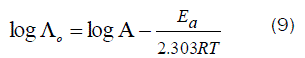
where A is the frequency factor, R is the gas constant and Ea is the Arrhenius activation energy of the transfer process. Consequently, from the plot of log (Λo) vs. 1/T, the Ea values can be evaluated [50-85] as shown in Fig (5&6) for (1:1) M to L stoichiometric complexes of CaCl₂ and ampicillin in water and in methanol, giving high activation energy value due to solvation behavior.

Figure 6: The relation between (log Λo) and (1/T) for (1:1) M to L stoichiometric complexes of CaCl₂ and ampicillin in methanol.

Table 4: The enthalpies (ΔH_f) and entropies (ΔS_f) of formation of CaCl₂ and ampicillin complexes in methanol at different temperatures.

Table 5: Activation energy (E_a), Gibbs free energy of activation (ΔG*) and entropy change of activation (ΔS*) for CaCl₂ and ampicillin (1:1) complexes in water at different temperatures.

Table 6: Activation energy (E_a), Gibbs free energy of activation (ΔG*) and entropy change of activation (ΔS*) for CaCl₂ and ampicillin (1:1) complexes in methanol at different temperatures.

Conclusion

This research focused on the study of thermodynamic complexation reactions between the ligand, ampicillin , with Ca²⁺ metal cation. The stability constants of the complex formation between ligand and metal cations was investigated by applying the conductometric method at different temperatures. Based on the results, the stability constant for the complexation reaction of Ca²⁺–ampicillin shows a decrease with increasing temperatures.

In this thermodynamic study, the negative sign of the ΔG_f shows that the ligand is capable of forming stable complexes and that the process will proceeding spontaneously, while the positive sign of the entropy shows that ΔS_f is the driving force of the complexation reaction in this complex formation. These facts mean that ΔG_f is always negative and ΔS_f is always positive.

References

1. Gabani S, Gianni P, Mollica V, Lepori L. Group contributions to the thermodynamic properties of non-ionic organic solutes in dilute aqueous solution. J Solution Chem. 1981; 10: 563-595.
2. Abraham MH, Whiting GS, Fuchs R, Chambers EJ. Thermodynamics of solute transfer from water to hexadecane. J ChemSoc Perkin Trans. 1990;2:291-300.
3. Cramer CJ, Truhlar DG. In Free Energy Calculation in Rational Drug Design, Reddy MR. Eds. Kluwer/Plenum: New York; 2001:63–95.
4. Morin RB. 1982. Gorman M., Chemistry and Biology of ß-lactam antibiotic. Academic Press, New York.
5. Page E. 1992. The Chemistry of ß-lactam. Blackie Academic and Professional, New York.
6. Tawarah KM, Mizyed SA. A conductance study of the association of alkali cations with 1,13-dibenzo-24-crown-8 in acetonitrile. J Solution Chem. 1989;18:387– 401.
7. Smetana AJ, Popov AI. On the influence of ionic strength on the equilibrium constant of an ion-molecule reaction. J ChemThermodyn. 1979;11:1145-1149.
8. Debye P, Hückel H. The theory of electrolyte II – The border law for electrical conductivity. Phys Z. 1923;24:305.
9. Takeda Y. Thermodynamic Study for Dibenzo-24-crown-8 Complexes with Alkali Metal Ions in Nonaqueous Solvents. Bull ChemSocJpn. 1983;56:3600–3602.
10. Zollinger DP, Bulten E, Christenhuse A, Bos, M, Van Der Linden WE. Computerized conductometric determination of stability constants of complexes of crown ethers with alkali metal salts and with neutral molecules in polar solvents. Anal ChimActa. 1987;198:207-222.
11. Takeda Y. Thermodynamic study for dibenzo-24crown-8 complexes with alkali metal ions in nonaqueous solvents. Bull ChemSocJpn. 1983;56:3600.
12. Dye JL, Nicely VA. A general purpose curve fitting program for class and research use. J Chem Educ. 1971;48:443.
13. Ives DJG. 1971, Chemical Thermodynamics, University Chemistry, Macdonald Technical and Scientific, New York.
14. El-Khouly AA, Gomaa EA, and Abou El-leef S. Conductometry and solubility study of Cd2+-Kryptofix-22 complexes in various hydroorganic solvents. Bull Electrochem. 2003;19(4):153-164.
15. El-Khouly AA, Gomaa EA, Abou El-leef S. Apparent association constants of HgCl2 in presence of kryptofix –22 in mixed aqueous-organic solvents. Bull Electrochem. 2003; 19(5):193-202.
16. Gomaa EA. AbouElleef EM, Mahmoud EH. Gibbs free energies for the solvation of KClO3 in DMF-H2O at 301.15 K. EurChem Bull. 2013; 2(10): 732-735.
17. Gomaa EA. Solubility and solvation parameters of barium sulphate in mixed ethanol-water mixtures at 301.15 K. Int J Mater Chem. 2012; 2(1): 16-18.
18. Gomaa EA, Al-Jahdali BM. Association of Cu(NO3)2 with Kryptofix-221 in mixed (MeOH-DMF) solvents at different temperatures. American J Fluid Dynam. 2011; 1(1): 4-8.
19. Gomaa EA. Solvation parameters of lead acetate in mixed, N,N-dimethylformamide–water mixtures at 298.15K. AnaleleUniversitate din Bucuresti-Chimie. 2010;19: 45-48.
20. Handbook of Chemistry and Physics. 91st ed. 2010–2011.
21. Marcus Y. “Ion Properties”, Dekker, New York. 1999.
22. Marcus Y. “Solvent mixtures”, Dekker, New York. 2005.
23. Kim JI, Brückl N. On the temperature dependence of solubilities of inert Gases from the scaled particle theory. Z PhysChem.NeueFolge. 1978; 110: 197-208.
24. Tawa GJ, Topol IA, Burt SK, Caldwell RA, Rashin AA. Calculation of the aqueous solvation free energy of the proton. J Chem Phys. 1998,109:4852.
25. Camaioni DM, Scherdtfeger CA. J PhysChem A. 2005;109: 10795.
26. Casey PK, Christopher JC, and Donald GT. Aqueous Solvation Free Energies of Ions and Ion-Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J PhysChem B. 2006; 110: 16066-16081.
27. Shen C, Hagiwara R, Mallouk TE, Bartlett N. Thermodynamic Aspects of the Remarkable Oxidizing Capabilities of Fluorine-Lewis-Fluoroacid Mixtures. ACS Symposium, Inorganic Fluorine Chemistry Ser. 1994; 555:26-39.
28. Kelly CP, Cramer CJ, Truhlar DG. Single-Ion Solvation Free Energies and the Normal Hydrogen Electrode Potential in Methanol, Acetonitrile, and Dimethyl Sulfoxide. J PhysChem B. 2007; 111(2): 408-422.
29. GomaaEsam A. Molal solubility, dissociation and solvation parameters for saturated benzoic acid solutions in various solvents. PhysChem Liq. 2012;50:279-283.
30. GomaaEsam A. Solubility and solvation parameters of barium sulphate in mixed ethanol-water mixtures at 301.15. Int J Mater Chem. 2012;2(1) :16-18.
31. GomaaEsam A. Electrical conductance of Cu(NO3)2 with Kryptofix-222 inmixed (MeOH-DMF) solvents at different temperatures. American J Environ Eng. 2012;2(3) :54-57.
32. GomaaEsam A. Thermodynamic and polarization parameters of dibenzo-18-crown-6 in mixed methanol-water solvents. American J Poly Sci. 2012;2(3):35-38.
33. GomaaEsam A. Solvation parameters for sodium oxalate in mixed ethanol-water solvents at 301.15K. EurChem Bull. 2013;1: 259-261.
34. GomaaEsam A AbouElleefElsayed, Mahmoud EA. Gibbs free energies for solvation of KClO3 in mixed DMF-H2O solvents at 301.15K. EurChem Bull. 2013;2:732-735.
35. GomaaEsam A, AbouElleefElsayed. Thermodynamics of the solvation of lead nitrate in mixed DMF-H2O solvents at 301.15K. American ChemSci J. 2013;3:489-499.
36. GomaaEsam A, AbouElleefElsayed. Thermodynamics of the solvation of potassium thiocyanate in mixed DMF-H2O solvents at 301.15K. Sci Technol. 2013;3:118-122.
37. GomaaEsam A, AbouElleefElsayed , Abdel RazekMG.Thermodynamics of the solvation of CaSO4 in mixed DMF-H2O solvents at 301.15K Int Res J Pure App Chem. 2013,3:320-329.
38. GomaaEsam A. The microscopic free energies of solvation for K+,Rb+ and Cs+ in mixed DMFA-water solvents at 298.15K, Int J TheorMathem Phys. 2013;3:151-154.
39. GomaaEsam A, Al Jahadali BA. Conductometric studies of calcium ions With Kryptofix 221 in mixed MeOH-DMF solvents at different temperatures. Education. 2012;2(3)37-40.
40. GomaaEsam A. Molal solubility, dissociation and solvation param- teres for saturated phenylalanine in various solvents at 298.15K. American J Biochem. 2012;2(3):25-28.
41. GomaaEsam A. Molal solubility, dissocation ,association and solvation parameters for saturated o-chlorobenzoic acid in various solvents at 298.15K. Food Public Health. 2012;2(3):65-68.
42. GomaaEsam A. Ionic Gibbs free energies,enthalpies and entropies of some ions in various solvents. Global Adv Res J Chem Mater Sci. 2012;1:35-38.
43. GomaaEsam A. The macroscopic and microscopic free energies of solvation of silver chromateand silver phosphate in some organic solvents at 298.15K. Frontiers Sci. 2012;2:24-27.
44. GomaaEsam A, AbouElleefElsayed M, Helmy ET, DefrawySh M, Solvent effects on the thermodynamics of solvation of barium diphenylaminesulfonate. Southern J Chem. 2013;21:1-10.
45. Gomaa EA , Ibrahim KM, Hassan NM. Conductometric study of complex formation between Cu(II) ion and 2-hyroxyimino-3-(2,-hydrazonopyridyl)-butane(HL). Frontiers Sci. 2012; 76-85.
46. Gomaa EA, Ibrahim KM, Hassan NM. Evaluation of thermodynamic parameters (conductometrically) for interaction of Cu(II) ion with 4-phenyl-1-diacetyl monoxime-3-thiosemicarbazone (BMPTS) in (60%V) ethanol water (EtOH-H2O) at different temperatures. The Int J Eng Sci. 2014, 3:44-51.
47. Gomaa EA, Abu El-Nader HM, RashedShE. Gibbs free energies for Interaction of CuCl2 with(E)-1-phenyl-2-92-94-9e0-phenyldiazenyl) Phenylhrazono)-2-(phenylsulfonyl) ethanone in ethanol at different Temperatures. The Int J Eng Sci. 2014;3: 64-73.
48. Gomaa EA, Ibrahim KM, Hassan NM. Thermodynamics of complex Forrmation (conductometrically) betweenCu(II) ion and 4-phenyl-1-diacet- yl monoxime-3-thiosemicarbazonein ethanol at different temperatures. Research and Reviews: Journal of Chemistry. 2014;3:47-55.
49. GomaaEsam A, AbouElleefElsayed M. Thermodynamics of solvation of barium diphenylaminesulfonate in ethanol-water mixed solvents. Thermal Power Eng. 2014;3 : 222-226.
50. GomaaEsam A, AbouElleefElsayedM,Elsayed T. HelmyElsayed T. Solvation of oxytetracycline hydrochloride in ethanol-water mixed solvents. Research and Reviews: Journal of Chemistry. 2014;3:22-27.
51. GomaaEsam A. Dissociation,association and solvation parameters for Saturated glycine in various solvents at 298.15K. Sci Technol. 2013,3:123-126.
52. GomaaEsam A. Thermodynamics of complex formation between Cu(II) and 4-phenyl-1-diacetyl monooxime-3-thiosemicarbazone in methanol. Research and Reviews: Journal of Chemistry. 2014; 3:28-37.
53. Gomaa EA, El-Askalany AH, Moussa MNH. Dissociation of KClin mixed hexamethylphosphortriamide-water solvents. Rev RoumChim. 1987;32 :243.
54. GomaaEsam A. Theoretical contribution of solvation of AgBr in some organic solvents at 25oC. ThermochimicaActa. 1988,128:99.
55. GomaaEsam A. Solubility of tetraphenyl derivatives in aqueous- hexamethylphosphortriamide solutions at 25oC. Indian J Tech.1986;24:725.
56. GomaaEsam A. Transfer free energies of ions from water to N,N,- dimethylformamide and its aqueous mixtures based on Ph4AsBPh4 and Ph4SbBPh4 assumptions. Thermochimica Acta.1989;142:19.
57. GomaaEsam A. Solvation free energies of K+,Rb+ and Cs+ ions in methanol-DMF mixtures. CroaticaChimicaActa. 1989, 62:475.
58. GomaaEsam A. Single ion free energies of some monovalent ions in mixed dimethylacetamide using the asymmetric Ph4AsBPh4 assumption. ThermochimicaActa. 1989;147:313.
59. Gomaa EA, Shallapy AM, Moussa MNH. Solute –solvent interaction of phenylalanine in various organic solvents. J Indian Chem Soc.1991;68:339.
60. Gomaa EA, Shallapy AM and Moussa MNH, Solvation of o- and p-nitoanilines in some organic solvents. Asian J Chem.1992;4:518.
61. Abu El-Nader HM and GomaaEA,Solvation of AgCl in mixed water- DMF solvents. Mansoura Sci Bull. (A Chem).1996;23 :1.
62. Kim JI, Cecal A., Born H.J., and Gomaa EA. Preferential solvation of single ion : a critical study of the Ph4AsBPh4 assumption for single ion thermodynamics in mixed aqueous-acetonitrile and aqueous-dimethyl formamide solvents. Z Physik Chemic NeueFolge. 1978;110: 209.
63. Kim JI, Gomaa EA. Preferential solvation of single ion : The Ph4AsPh4B assumption for single ion thermodynamics in mixed dimethylsulphoxide-water solvents. Bull SocChim Belg.1981;90:391.
64. Gomaa EA, El-Khouly AA, Mousa MA. Association of salicylic acid in acetonitrile – water media, Indian J Chem. 1984;23:1033.
65. Gomaa EA, Mousa MA, El-KhoulyAA,Gibbs free energies of solute- solvent interactions for salicylic,sulphosalicylic and sulphanilic acids in various solvents. ThermochimicaActa. 1985;86 :351.
66. Gomaa EA, Mousa MA, El-Khouly AA. Association, dissociation and hydrogen bonding of salicylic acid in water-N,N-dimethylformamide mixtures. ThermochimicaActa. 1985;89:133.
67. GomaaEsamA,Single ion thermodynamics for Cl-, Br- , I-, Ph4B-, K+, Rb+ Cs+ and Ph4As+ in mixed hexamethylphosphortriamide-water Solvents. ThermochimicaActa. 1985;91:235.
68. GomaaEsam A. Study of Ph4SbBPh4 assumption for single ion free energies in some organicsolvents. Thermochimica Acta.1989;140:7.
69. GomaaEsam A. Study of the asymmetric Ph4AsBPh4 assumption for the evaluation of single ion free energies in mixed N-methylpyrrolidone-water solvents. Bull SocChim Fr. 1989;5:620.
70. GomaaEsam A. Preferential solvation of Ph4AsBPh4 and Ph4SbBPh4 in mixed DMSO/DMF solvents. Bull Soc ChimFr.1989;5:623.
71. GomaaEsam A. Free energies of transfer for some monovalent ions and Ph4SbBPh4 from water to acetonitrile-water mixtures using the asymmetric Ph4AsBPh4 assumption. ThermochimicaActa. 1989,152:371.
72. Shehatta IS, El-Askalany AH, Gomaa EA. Thermodynamic parameters of transfer and solution of oxalic acid in dimethylsulphoxide- water media. ThermochimicaActa. 1993;219:65.
73. EA Gomaa, G Begheit. Polarographic and conductometric studies of uranyl ion in sulphuric acid-ethanol media. Asian J Chem. 1990;2:444.
74. El-Khouly AA, Gomaa, EA, and Abou-El-Leef S, Conductivity and Solubility studies of (Cd-Kryptofix-22) complexes in various hydooganic solvents. Bull Electrochem. 2003;19:153.
75. Hamada MA, Gomaa EA, El-Shishtawi NA. Optomechanical properties of 10% PVA in presence ofCoCl2 and 44% ethanol-water composition. Int J Optoelectronic Eng. 2012;1:1-3.
76. Ibrahim Kamal M, GomaaEsam A, Zaky Rania R, Abdel El-Hady MN. The association and formation constants for CuCl2 stoichiometric complexes with (E)-3-oxo-N-(thiazol-2-yl)propanamide in absolute ethanol solution. American J Chem. 2012,2:23-26.
77. El-Khouly AA , Gomaa EA and Salem SE. Conductometric study of complex formation between 2,3 –pyrazinedicarboxylic acid and some transition metal ions in methanol. Southern Brazilian J Chem. 2012;20:43-50.
78. Gomaa EA and Al –Jahdali BAM. Electrical conductance of Cu(NO3)2 with Kryptofix-222 in mixed (MeOH-DMF) solvents at different temperatures. American J Environ Eng. 2012;2:6-12.
79. Gomaa EA, El-Askalany AH, Moussa MNH. Polarographicelectroreduction of uranyl on in glycine,Dl-Aspartic acid and phenylalanine. Asian J Chem. 1992;4:553.
80. GomaaEsam A. Application of the scaled particle theory for the solvation of silver tetraphenyl boride in dimethylformamide-water mixtures at 298.15K. J King Saud Uni. 1991;3(1):69.
81. GomaaEsam A. Excess volumes aandexess dielectric constant of the mixed solvents : MeOH-DMF,MeOH-DMSO ,DMSO-DMF. Oriental J Chem.1990;6:12.
82. Gomaa EA, Hamada MA and Galal R. Apparent molal volumes of sodium fluoride in mixed aqueous-ethanol solvents. Avances en Quimica. 2010;5(2):117-121.
83. GomaaEsam A. Solvation parameters of lead acetate in mixed N,N-dimethylformamide mixtures at 298.15K,Analele Uni.dinBucuresti-Chimie. 2010;19(1):45-48.
84. El-ShishtawiNagah A, Hamada Maany A, GomaaEsam A. Influence of permanent magnet on the association constants of FeCl3+ 10% PVA in 50% ethanol-water solutions ,conducometrically
85. at 298.15K.Phys Chem. 2011;1(1):14-16.
86. Gomaa EA and Al Jahdali BAM. Condutometric studies of ionic association of divalent electrolyte Cu(NO3)2 with Kryptofix-22 in mixed MeOH-DMF solutions at different temperatures. American J Condenesed Matter Physics. 2012;2(1):16-21.