ISSN: 2320-2459
ISSN: 2320-2459
1Department of Physics, Jimma University, Jimma, Ethiopia
Received date: 18/06/2015 Accepted date: 19/08/2015 Published date: 21/08/2015
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
We analyze density operator, Q function, photon statistics, quadrature squeezing, and Cv entanglement that holds true for a pair of superposed two-mode photon system. We also present a slightly modified definition of entanglement and squeezing for a pair of super- posed two-mode system and new definition for degree of entanglement. In order to carry out our analysis, we consider a quantum system with Gaussian variables with zero mean. It is found that maximum degree of entanglement as well as squeezing occurs at steady-state and threshold.
Bipartite, Density Operator, Entanglement, Squeezing PACS numbers: 42.50.Dv, 42.65.Y, 42.50.Ar, 42.50.Ct
In recent years, the topic of continuous-variable entanglement has received a significant amount of attention as it plays an important role in all branches of quantum information processing [1]. The efficiency of quantum information schemes highly depends on the degree of entanglement. A two-mode subharmonic generator at and above threshold has been theoretically predicted to be a source of light in an entangled state [2,3]. Recently, the experimental realization of the entanglement in two-mode subharmonic generator has been demonstrated by Zhang et al. [4]. In a two-mode subharmonic generator, a pump photon of frequency ωc is down converted into highly correlated signal and idler photons with frequencies ωa and ωb such that ωc= ωa + ωb [5]. A detailed analysis of the quadrature squeezing and photon statistics of the light produced by a subharmonic generation has been made by a number of authors [1,6-8]. It has been shown theoretically [9-12] and subsequently confirmed experimentally [13,14] that subharmonic gen- eration produces a light that has a maximum of 50% squeezing below the coherent state level.
On the other hand, Xiong et al. [15] have recently proposed a scheme for an entanglement based on a non-degenerate three-level laser when the three level atoms are injected at the lower level and the top and bottom levels are coupled by a strong coherent light. They have found that a non- degenerate three-level laser can generate light in entangled state employing the entanglement criteria for bipartite continuous-variable states [15].
Moreover, Tan et al. [16] have extended the work of Xiong et al. and examined the generation and evolution of the entangled light in the Wigner representation using the sufficient and necessary in separability criteria for a two-mode Gaussian state proposed by Dual et al. [15] and Simon [17]. Tesfa [18] has considered a similar system when the atomic coherence is induced by superposition of atomic states and analyzed the entanglement at steady-state. Furthermore, Ooi [19] has studied the steady-state entanglement in a two-mode Λ laser. More recently, Eyob [20] has studied continuous-variable entanglement in a non-degenerate three-level laser with a parametric amplifier.
Even though Einstein, along with his colleagues Podolsky and Rosen, was first to recognize the criterion for analyzing entanglement condition for a two-mode light beams [21], a significant number of works have not been devoted on a pair of superposed two-mode light beams.
In this paper, we present slightly modified definitions of entanglement and squeezing for a pair of superposed two-mode system and new definition for degree of entanglement. Moreover, we also formulate the photon statistics, quadrature squeezing, the density operator, and the Q function that holds true for all a pair of superposed two-mode photon system. In order to carry out our analysis, we consider a quantum system with Gaussian variables with zero mean.
The Density Operator
Here we seek to determine the density operator for a pair of superposed two-mode light beams. Suppose 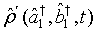 is the density operator for a certain two mode light beam. Then upon expanding this density operator in normal order
is the density operator for a certain two mode light beam. Then upon expanding this density operator in normal order
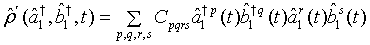 (1)
(1)
and employing the completeness relation for a two-mode coherent-state
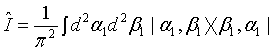 (2)
(2)
one easily finds
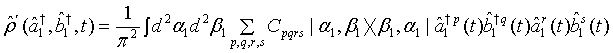 (3)
(3)
in which 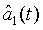 and
and 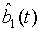 are the annihilation operators for the first and second light modes, respectively. This expression can be rewritten as
are the annihilation operators for the first and second light modes, respectively. This expression can be rewritten as
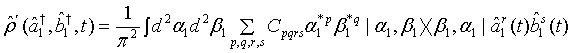 (4)
(4)
Applying the relation
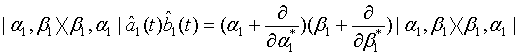 (5)
(5)
one easily obtains
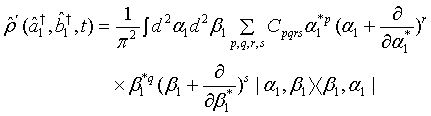 (6)
(6)
there follows
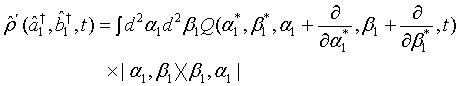 (7)
(7)
In view of (7), the density operator for the first light beam can be rewritten using the displacement operator as
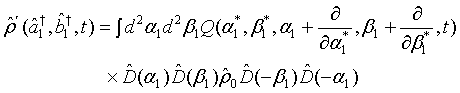 (8)
(8)
in which 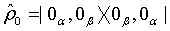
Now we realize that the density operator for the superposition of the first light beam and another one is expressible as
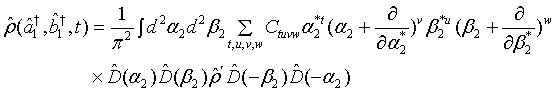 (9)
(9)
so that in view of Eq. (7), we have
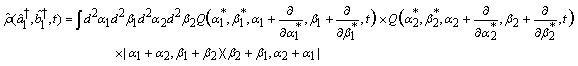 (10)
(10)
We now define the Q function for the superposition of two-mode light beams as
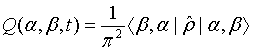 (11)
(11)
Then employing Eqs. (10) and (11) as well as applying the binomial theorem, the Q function for a pair of superposed twomode light beams can be written as
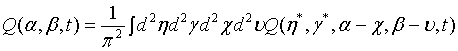
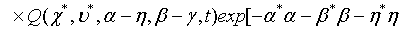
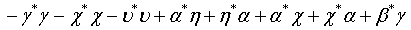
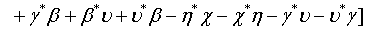 (12)
(12)
Furthermore, the expectation value of an operator 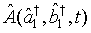 can be expressed in the form
can be expressed in the form
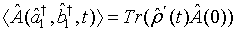 (13)
(13)
Introducing (7) in (13), we find
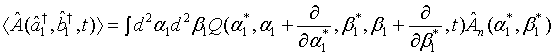 (14)
(14)
in which 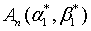 is the c-number function corresponding to
is the c-number function corresponding to 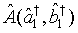 in the normal order.
in the normal order.
Moreover, we seek to derive an alternative expression for the expectation value of a given opera- tor representing two-mode light beam. To this end, applying the completeness relation given by Eq. (2) in (1) twice, we have
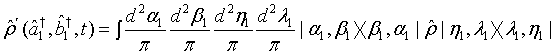 (15)
(15)
This can be rewritten as in the form
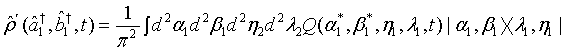 (16)
(16)
in which
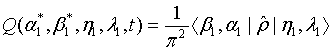 (17)
(17)
Therefore, in view of (13) and (16), the expectation value of a given operator function 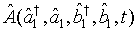 is expressible as
is expressible as
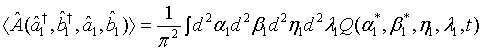
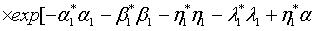
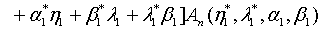 (18)
(18)
where
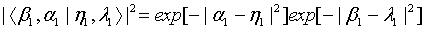 (19)
(19)
with 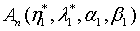 is the c-number function corresponding to
is the c-number function corresponding to 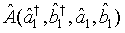 in the normal order.
in the normal order.
On the other hand, it is convenient to write the Q functions of the two separate two-mode sub- harmonic light beams. Thus with the aid of Kassahun [5], the Q function for the first signal-idler modes can be written as
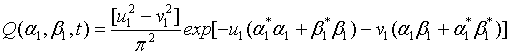 (20)
(20)
And the Q function for the second signal-idler modes can be written as
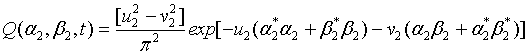 (21)
(21)
Photon Statistics
In this section, we seek to study the statistical properties of a pair of superposed two-mode light beams.
The mean photon number
The mean photon number for a pair of superposed two-mode light beams in terms of density operator can be expressed as
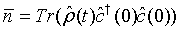 (22)
(22)
where 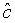 represents the annihilation operator for a pair of superposed two-mode light beams. Thus introducing Eq. (10) into Eq. (22), we have
represents the annihilation operator for a pair of superposed two-mode light beams. Thus introducing Eq. (10) into Eq. (22), we have
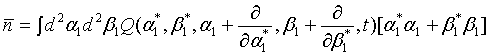
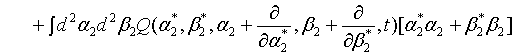
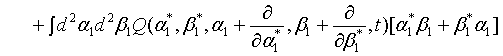
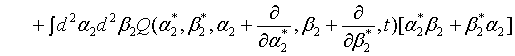
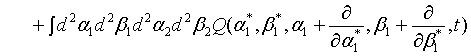
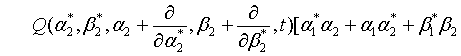
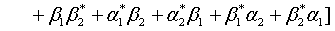 (23)
(23)
Then on account of Eq. (14), Eq. (23) can be put in the form
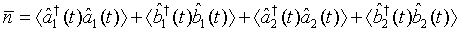
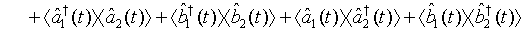
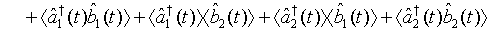
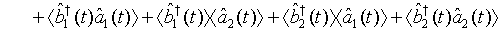 (24)
(24)
where 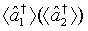 and
and 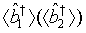 are the annihilation operators representing the first and the second one-mode light beam of system one (two), respectively. For the case in which
are the annihilation operators representing the first and the second one-mode light beam of system one (two), respectively. For the case in which 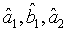 and
and 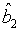 are Gaussian operators with zero mean, we see that
are Gaussian operators with zero mean, we see that
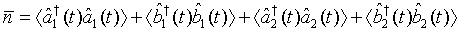
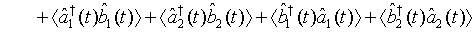 (25)
(25)
with the commutation relation
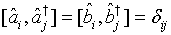 (26)
(26)
which holds true for a one-mode light beam.
For instance, the mean photon number of a pair of superposed two-mode sub harmonic light beams, at steady-state, turns out to be
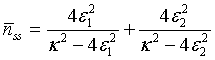 (27)
(27)
We see that the global mean photon number for a pair of superposed two-mode sub harmonic light beams is the sum of the mean photon numbers of the separate two-mode sub harmonic light beams. And the plot in Figure 1 shows that maximum mean photon number is observed when the cavity light operating at threshold.
The photon- number variance
We next proceed to determine the variance of the photon number for a pair superposed two- mode light beams. Then we define the photon-number variance for a pair of superposed two-mode light beams as
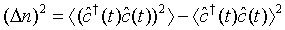 (28)
(28)
Now using the commutation relation
we find
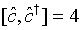 (29)
(29)
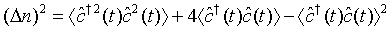 (30)
(30)
We note that 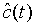 is a Gaussian operator with zero mean. Hence we see that
is a Gaussian operator with zero mean. Hence we see that
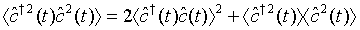 (31)
(31)
Thus one can put Eq. (30) in the form
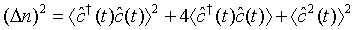 (32)
(32)
Then the annihilation operator representing a pair of superposed two-mode light beams can be written as with the commutation relation
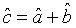 (33)
(33)
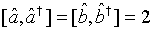 (34)
(34)
which holds true for a pair of superposed one-mode light beams [22]. Applying Eq. (33) and its complex conjugate in Eq. (32), we obtain
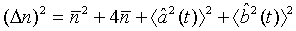
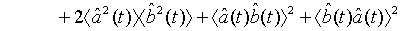
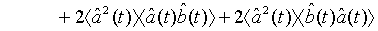
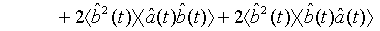
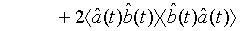 (35)
(35)
where n is the mean photon number of a pair of superposed two-mode light beams.
Moreover, taking a particular system, the global variance of the photon number for a pair of superposed two-mode sub harmonic light beams, at steady-state, turns out to be
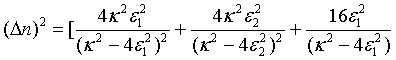
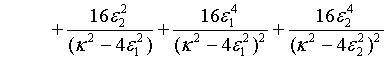
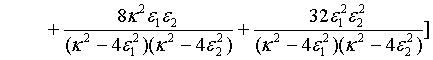 (36)
(36)
This shows that unlike that of the mean photon number, the global variance of the photon number for a pair of superposed two-mode sub harmonic light beams is not the sum of the global variance of the photon number for the separate two-mode sub harmonic light beams [23].
Photon number correlation
We next proceed to calculate the photon number correlation for a pair of superposed two-mode light beams. The photonnumber correlation for a pair of superposed two-mode light beams can be defined as
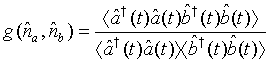 (37)
(37)
Since 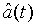 and
and 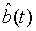 are Gaussian variables with zero mean, the photon number correlation can be rewritten as
are Gaussian variables with zero mean, the photon number correlation can be rewritten as
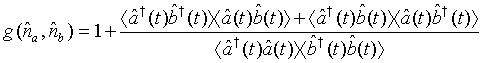 (38)
(38)
Furthermore, the photon-number correlation for a pair of superposed two-mode sub harmonic light beams reduced to
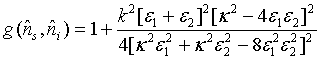 (39)
(39)
We immediately observe that the photon numbers for a pair of superposed two-mode cavity light beams are highly correlated.
Quadrature squeezing
Here we determine the quadrature squeezing for a pair of superposed two-mode light beams. We define the quadrature variance for a pair of superposed two-mode cavity light beams by
where
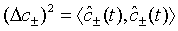 (40)
(40)
and
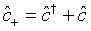 (41)
(41)
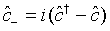 (42)
(42)
are the plus and minus quadrature operators for the superposed two-mode cavity light. With the aid of the commutation relation described by Eq. (29), Eq. (40) can be put in the form
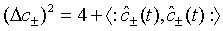 (43)
(43)
We note that 4 being the quadrature variance of a pair of superposed two-mode vacuum state. Then employing Eq. (41) and Eq. (42), Eq. (43) leads to
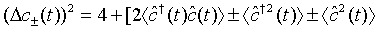
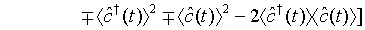 (44)
(44)
In view of the fact that cˆ(t) is Gaussian operator with zero mean, Eq. (44) reduces to
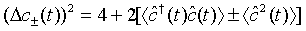 (45)
(45)
Applying Eq. (33) in Eq. (45), we have
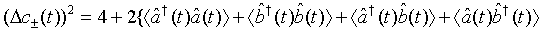
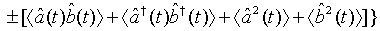 (46)
(46)
At steady state, this expression for a pair of superposed two-mode sub harmonic light beams, turns out to be
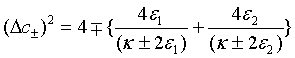 (47)
(47)
It is not hard to see that a pair of superposed two-mode sub harmonic light beams is in two-mode squeezed states and squeezing occurs in the plus quadrature.
Next we determine the quadrature squeezing for a pair of superposed two-mode light beams relative to the quadrature variance for a pair of superposed two-mode vacuum state. We define the quadrature squeezing of a pair of superposed two-mode cavity light beams by
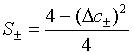 (48)
(48)
Here we consider a pair of superposed two-mode subharmonic light beams. Then quadrature squeezing, at steady-state, found to be
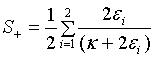 (49)
(49)
This shows that the global quadrature squeezing of a pair of superposed two-mode subharmonic light beams is the average of the quadrature squeezing of the separate two-mode subharmonic light beams. The plot in Figure 2 shows that the light generated by a pair of superposed two-mode light beams is in a squeezed state, with maximum quadrature squeezing being 50% below the coherent level. This occurs when the system under consideration is operating at 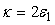 and
and 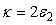 .
.
Entanglement
In this section we seek to study the entanglement condition for a pair of superposed two-mode light beams. Hence in order to show the entanglement of a pair of superposed two-mode cavity light beams, we apply the criterion presented in Ref. [15]. On the basis of this criterion, a pair of superposed cavity light beams is said to be entangled if the sum of the variance of the two EPR-like operators sˆ and tˆ satisfies the inequality
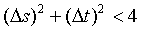 (50)
(50)
where
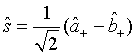 (51)
(51)
with
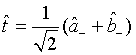 (52)
(52)
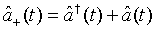 (53)
(53)
and
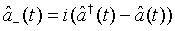 (54)
(54)
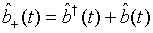 (55)
(55)
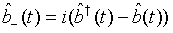 (56)
(56)
The variance of the operators sˆ and tˆ can be expressed as
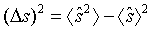 (57)
(57)
and
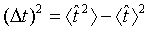 (58)
(58)
In view of the fact that aˆ(t) and bˆ(t) are Gaussian variables with zero mean and employing Eqs. (53), (55), and (57), one can readily obtains
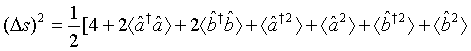
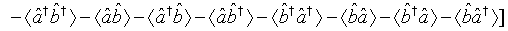 (59)
(59)
Following the same procedure, we get
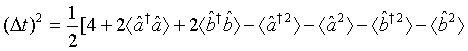
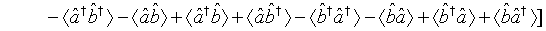 (60)
(60)
On account of Equations (59) and (60), we see that the sum of the variance of the two EPR-like operators to be
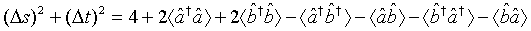 (61)
(61)
Finally, we define the degree of entanglement as
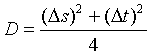 (62)
(62)
For instance, the sum of the variance of the two EPR-like operators for a pair of superposed two- mode sub harmonic light beams to be
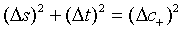 (63)
(63)
Moreover, in view of Equations (47) and (63) at steady-state and threshold, the sum of the variance of the two EPR-like operators to be
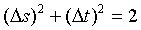 (64)
(64)
On the basis of the criteria Equation (50), we clearly see that a pair of superposed two-mode sub- harmonic light beams are entangled at steady-state and the plot in Figure 3 shows that maximum entanglement turned out be observed in the squeezed photon-state with 50% degree of entanglement when the light operating at steady-state and threshold [24].
We have analyzed density operator, Q function, photon statistics, quadrature squeezing, and Cv entanglement that holds true for a pair of superposed two-mode photon system. We have also presented slightly modified definitions of entanglement and squeezing for a pair of superposed two-mode cavity light and new definition for degree of entanglement. In order to carry out our analysis, we considered a quantum system with Gaussian variables with zero mean. It is found that the mean photon number of a pair of superposed two-mode light beams to be the sum of the mean photon numbers of the constituent light beams. However, the photon number variance of a pair of superposed two-mode light beams does not happen to be the sum of the photon number variances of the separate light beams.
Furthermore, applying a slightly modified definition of the quadrature variance, we have obtained that the quadrature variance of a pair of superposed two-mode light beams to be the sum of the quadrature variances of the individual light beams and the superposed two-mode light beams are in a squeezed state and the squeezing occurs in the plus quadrature. Moreover, the quadrature squeezing turned out to be the average of the quadrature squeezing of the component light beams. Besides, our analysis shows that at steady state and at threshold, the super- posed two-mode light beams have a maximum squeezing of 50% below the two-mode vacuum-states level. We have also clearly shown that a pair of superposed two-mode light beams is entangled at steady-state and the entanglement turned out to be observed in the highly correlated squeezed photons with 50% degree of entanglement.
To this end, we would like to mention that the predictions made in this paper concerning the entanglement and quadrature squeezing to be experimentally verified.