ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Prof.Laila Beebi M1 ,Vishakh,K H2, Naveen N2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper presents the control of the longitudinal dynamics of a reusable launch vehicle in its re-entry phase. The control of longitudinal dynamics mainly consists of the pitch angle control. Here the pitch is controlled using an Linear Quadratic Regulator controller. The feedback LQR controller is compared with a classical PID controller. The launch vehicle model is controlled using the designed LQR controller.
Keywords |
||||||||
| Euler Angles, Linear Quadratic Regulator, Reusable Launch Vehicle. | ||||||||
INTRODUCTION |
||||||||
| The Longitudinal dynamics of a Reusable launch vehicle is being addressed here. These Reusable Launch Vehicles, or RLV's, are space vehicles designed to perform multiple missions. RLV's, due to the fact that they are re-used, will dramatically reduce the cost of access to low earth orbit. However, the technical challenges of designing a system to y to orbit and return are monumental. For example, the entire Saturn V rocket was expended while sending humans to the Moon. On the other hand, the Space Shuttle, which transports astronauts to Low Earth Orbit and back, is reused over and over again. The control of the Reusable Launch Vehicle is one of the major challenges facing today. Development of the Reusable Launch Vehicle (RLV) technology is a pioneering step in this direction. Such a launch vehicle, if developed successfully, will not only be a major technological breakthrough, but would also yield rich economic dividends for future space programs. | ||||||||
| The pitch of the vehicle is to be controlled exactly with high percentage accuracy. The control of pitch angle by controlling the elevator deflection of the Reusable launch vehicle is a challenging problem. The controller must be very much robust so that the under any uncertainties the pitch control should be successful. The uncertainties or disturbances present during the flight are unpredictable since a lot factors are affecting. So the controller must be susceptible to whatever disturbance it may be facing | ||||||||
| In 2009 Yuri B Shessel and Dan Daniels in their paper Reusable Launch Vehicle Attitude Control Using a Time Varying Sliding Mode Control technique in ascent and entry Flight phases describes about the Time Varying Sliding Mode Control which commands Euler roll, Pitch and Yaw angles in the ascent flight and it controls bank attack and slid slip. The design problem is then to select the parameters of each of the structures and to define the switching logic. A variable structure system can possess new properties not present in any of the structures used. For instance an asymptotically stable system may consist of two structures neither of which is asymptotically stable. He shows many examples where new system properties are obtained by composing a desired trajectory from the part of trajectories of different structures. | ||||||||
| This paper presents some classical controllers for controlling the reentry phase of a reusable launch vehicle in its reentry phase. An LQR controller is compared with a PID controller with its response and settling time. The Longitudinal dynamics is only addressed which consists of the pitch control. The elevator is adjusted to get the desired pitch response. This paper is organized as follow: Section I gives the Introduction of the Pitch control of Reusable Launch Vehicle. Section II is helpful to understand the Methodology of related work. Section III explains the Simulation Result. Section IV concludes the paper and followed by the references. | ||||||||
METHODOLOGY |
||||||||
A. RLV Modeling |
||||||||
| The equations governing the motion of an aircraft are a very complicated set of six non-linear coupled differential equations. However, under certain assumptions, they can be decoupled and linearised into the longitudinal and lateral equations. Pitch control is a longitudinal problem, and in this example, we will design an autopilot that controls the pitch of an aircraft. | ||||||||
| Assume that the aircraft is in steady-cruise at constant altitude and velocity; thus, the thrust and drag cancel out and the lift and weight balance out each other. Also, assume that change in pitch angle does not change the speed of an aircraft under any Circumstance (unrealistic but simplifies the problem a bit). Under these assumptions, the longitudinal equations of motion of an aircraft can be written as a state space equation consisting of the states pitch, pitch rate and angle of attack. The pitch is controlled mainly here using the elevator as the input. so the input part of the state space equation consists of a elevator deflection. The output equation consists of a matrix that multiplied with the state matrix will get the pitch as the output. We can give the disturbance part any functional values. | ||||||||
B Classical Controller Design |
||||||||
| [1] LQR Controller | ||||||||
| LQR controller is a feedback controller. In a feedback controller the states or output is feedback and is compared to the set point value. According to the error the output or the states are changed. So in an LQR controller the output is feedback via a controller gain K. our purpose is to design the LQR controller gain so that we get the desired response. | ||||||||
| In the design of an LQR controller we normally come across the cost function | ||||||||
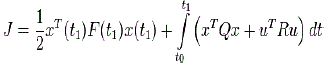 |
||||||||
| So here if we find out Q and R according to the cost function the we can easily find the gain matrix K by the MATLAB command lqr(A,B,C,D,Q,R). After finding the gain value K we need to change the input as | ||||||||
| [2] PID Controller | ||||||||
| A proportional–integral–derivative controller (PID controller) is a generic control loop feedback mechanism(controller) widely used in industrial control systems – a PID is the most commonly used feedback controller. A PID controller calculates an "error" value as the difference between a measured process variable and a desired set point. The controller attempts to minimize the error by adjusting the process control inputs. | ||||||||
| The PID controller calculation (algorithm) involves three separate constant parameters, and is accordingly sometimes called three-term control the proportional the integral and derivative , values denoted P, I, and D. Heuristically, these values can be interpreted in terms of time: P depends on the present error, I on the accumulation of past errors, and D is a prediction of future errors, based on current rate of change. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, or the power supplied to a heating element. | ||||||||
| In the absence of knowledge of the underlying process, a PID controller has historically been considered to be the best controller. By tuning the three parameters in the PID controller algorithm, the controller can provide control action designed for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoots the set point and the degree of system oscillation. Note that the use of the PID algorithm for control does not guarantee optimal control of the system or system stability. | ||||||||
SIMULATION RESULT |
||||||||
| In the design of the LQR controller we got the gain value as | ||||||||
| Here the step signal of 0.1 was given as input and the step time was 1 sec. The steady state error was very less. The settling time was below 3 sec. | ||||||||
| While with PID controller the pitch control was obtained as | ||||||||
| Here we gave a step of 1 and step time was 0 sec. The output we got was more faster settling below 2 sec but the settled value was not fully accurate. But for fast response it can be used | ||||||||
CONCLUSION |
||||||||
| Here we have compares the two classical controller design for the pitch control of a Reusable Launch Vehicle. The PID controller and the LQR controller are designed and the response of these two controllers was studied. They both had their advantages and disadvantages for each of them. | ||||||||
Figures at a glance |
||||||||
|
||||||||
References |
||||||||
|