International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

CONTROL OF THE PORTABLE FUEL CELL CHARGER USING CUK CONVERTER

Tae-Hoon Kim1, Nguyen Van Sang1, and Woojin Choi2
  1. Student, Dept. of Electrical Engineering, Soongsil University, Seoul, Republic of Korea1
  2. Associate professor, Dept. of Electrical Engineering, Soongsil University, Seoul, Republic of Korea2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

As power consumption of portable electronic equipment rapidly increases; the need of chargers using fuel cell which has higher energy density than that of secondary battery is raised. Most chargers developed so far are mainly buck-type converters, however, if fuel cell is used the battery should be charged with an increased voltage level through boost-type converter. In addition, unlike resistive load if batteries are controlled by general method, they induce large ripple current and have bad influence on the efficiency and life cycle of the batteries. Therefore, the selection of appropriate topology and control method is very important. In this paper a method of control for portable fuel-cell charger using small PEM (Proton Exchange Membrane) fuel cell stack and Cuk converter is proposed and the feasibility of it is verified through the experiments.

Keywords
PEM fuel cell, Battery Charger, Cuk Converter, Lithium-Polymer Battery, CC/CV mode charge

INTRODUCTION
As power consumption of portable electronic equipment rapidly increases, the need of chargers using fuel-cell which has higher energy density than that of secondary battery is raised. In the future, tiny fuel cells can potentially replace batteries in the next generation of portable electronics, such as laptop computers due to their high energy density and longer operation time. A compact methanol cartridge can be developed into a fuel cell package that can power electronic devices for three to five times longer than conventional batteries, though they can be accommodated in containers of the same size and weight. Such systems can be recharged by simply refilling the fuel cartridges, and existing research shows these fuel cells to be more environmentally friendly.
Most chargers developed so far are of On-Grid method and have decreasing voltage level by the buck-type converter with a rectifier and a filter capacitor [1-2]. However, if fuel cell is used, the battery often need to be charged increasing voltage level through boost-type converter due to the inherent low voltage characteristics of the fuel cell [3].It may be possible to use a buck-type converter with transformer. However, since chargers used for portable electronic equipment require miniaturization, a boost-type non-isolated converter can be selected as an appropriate topology. Unlike the pure resistive load, since Lithium-Polymer batteries have a huge capacitance and a small resistance inside, when they are charged by a non-isolated topology such as boost converter, higher value of the ripple current may flow through the battery depending on the impedance of the battery and the output capacitor. It is also well known that the large ripple current may cause a bad influence on the efficiency and life cycle of the batteries [4].
Cuk converter includes an inductor at the output like the buck converter, but unlike the boost converter, continuous current flows in the output [5]. Also, Cuk Converter allows stepping up the voltage by varying the duty ratio of the switch, thus it is suitable for the charge converter applications for the fuel cell.
In this paper control of the portable fuel cell charger using a fuel cell stack and a non-isolated Cuk converter is described and frequency characteristics of the Cuk converter is analyzed by the state-space modeling technique considering equivalent impedance of the battery. The battery is charged through the constant current mode (CCM) and constant voltage mode (CVM) by the dual control loop, which controls both the converter output voltage through an outer control loop and its input control through an inner control loop. The developed charger and its control algorithm will be verified through CCM/CVM charge by the experiments, respectively.

CHARACTERISTICS OF LITHIUM POLYMER BATTERY AND EQUIVALENT IMPEDANCE MODEL

A. Charging Method for the Lithium Polymer Battery
The general characteristic of a lithium polymer battery is as shown in Table I. The final discharge voltage is 3V per cell and a maximum voltage after full charge is in between 4.1V to 4.3V per cell. Typically it is charged by using CC (Constant Current) mode in the initial stage. When the battery voltage reaches to the full voltage, CV (Constant Voltage) mode is then used [6]. In CC Mode, the battery is charged with 1C-rate permitted by the manufacturer and the battery's voltage rises in this stage. When the terminal voltage of the battery reaches to the maximum level, the charger changes its mode to CV mode and the charge current is exponentially decreased and the voltage maintains at a constant value.

B. Equivalent Impedance Model of the Lithium Polymer Battery
To design a charge system for the lithium polymer battery, it is required to get an equivalent impedance model of the Li-Polymer battery.
Many equivalent circuit models exist for the lithium polymer battery. However, in this study, the model was simply developed as the modified Randle model by a series resistance, capacitance and an equivalent voltage source as shown in Fig. 2 [7]. The initial voltage of the Cb is 0 and VDC represents an initial voltage of the lithium polymer battery. The lithium polymer battery used in this study is AL3N5548135C-R-PCM by Exa Energy of which nominal capacity is 4000mAh, nominal voltage 11.1V, lower limit of the discharge voltage 9.0V, and higher limit of the charge voltage 12.6V.
The capacitance Cb of the equivalence circuit model can be calculated from Q=CV equation. In this study, the capacitance value of the battery was calculated as 4,000F as (1).
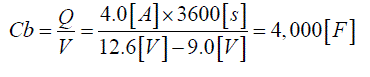image(1)
The series resistance Rb may be drawn from the time constant τ and capacity Cb, both from the real battery's CV Mode current profile. In this study, the time constant was calculated as 1,834 seconds and the series resistance Rb as 460mΩ as shown in (2).
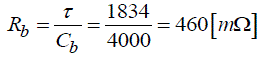image(2)

MODELING OF THE CUK CONVERTER CONSIDERING BATTERY IMPEDANCE
In this study, a state space averaging method was employed for the modeling of the Cuk converter taking into account the internal impedance of the battery. Fig. 4 shows the Cuk converter including equivalent impedance of the battery and the state equations of the converter can be simply described in a matrix form as (3).
image(3)
State variables at this time are the inductor current and capacitor voltage. Typically, the state equation for the Cuk converter with pure resistive load has more than 4 variables [8-9], but there are 5 state variables in total when the equivalence impedance of the battery is considered. Therefore, a state vector is equivalent to
image
The coefficient matrix of the state equation (A, B, C and E) can be derived by averaging the state equation at each state when the switch is on and off. Thus, the small signal model may be drawn from the state equation as (4).
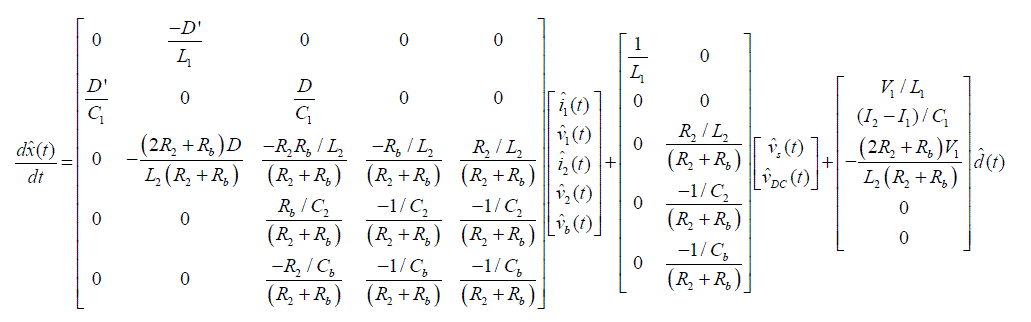image
In the equation (4), values expressed in “^” refer to as a small AC variation near the fixed operating point. Equation (4) at this time includes three independent input vectors: input voltage vˆs (t) , equivalent voltage source of the battery vˆDC (t) , and duly ratio dˆ (t) . However, since the frequency of the variation in the input voltage and the equivalent voltage source of the battery are far lower than that of the switching frequency, equation (5) can be derived from equation (4) by assuming that the small AC variation is equal to zero.
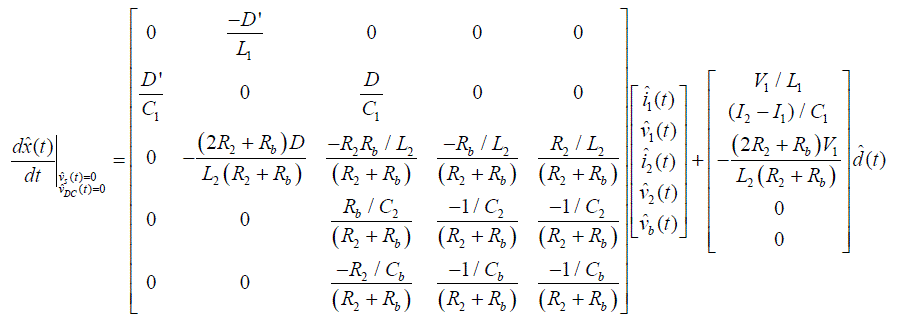image
Equation (6) and (7) show the input current control transfer function, Gid and output voltage control transfer function, Gvd, respectively. Both can be derived by Laplace transforming the state equation (5) and applying the parameter values in the Table II.
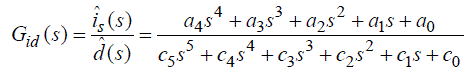image
where,
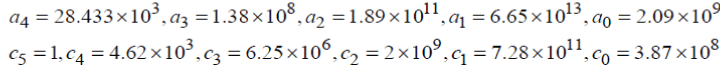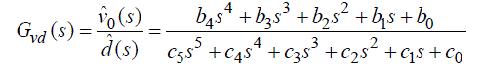image
image
image
In order to verify the derived transfer functions in (6) and (7) AC sweep was performed on the model of the system by PSIM and the resulting Bode plots were compared with the Bode plots drawn by the Matlab. As can be seen in Fig. 6 through Fig. 9 that the results for the current control transfer function and voltage control transfer function are well matched thereby proving that the derived functions are correct.Fig. 10 shows the pole-zero maps for the current control transfer function. A current control transfer function is a 5th order system that includes 5 poles and 4 zeroes, and has one resonant frequency due to a pole pair.As seen in the Fig. 10, current control transfer function is the minimum-phase system having all the poles and zeroes in the left-half plane and it has enough phase margin.Fig. 11 indicates a polezero map of the voltage control transfer function. Like the current control transfer function, it is also a 5th order system that includes 5 poles and 4 zeroes, but has 2 resonant frequencies due to a pair of poles and a pair of zeroes. Since it is a non-minimum phase system with a pair of zeroes located in the right-half plane, it has no phase margin [10], [11].

DESIGN OF THE CHARGER CONTROLLER
In this study, a double control loop is used for the charge controller. It consists of an inner loop for the current control and outer loop for the voltage control as shown in Fig. 12. Such double control has an advantage that it is not required to implement the controllers for each charge mode (CC and CV), respectively, thereby making the control algorithm simple.
In the outer voltage control loop, reference voltage, nominal voltage of the battery pack, is compared to the voltage feedback and creates current reference for the current control. At this time, the current reference is limited so that the charge current does not exceed an allowed charge current value (1C-rate in this case). The reference current command from the voltage controller is then compared to the feedback of the inductor current to generate the current error and it is used for the current controller to adjust the duty of the switch through the comparator. At this time, a closed-loop transfer function for the current control can be expressed by (8) and the closed-loop voltage transfer function that includes current control can be expressed by (9) [12].
image
image
Where, Gic is the current controller gain, Hi is the current feedback gain, 1/ m V is the comparator gain, Gvc is the voltage controller gain and Hv is the voltage feedback gain.

A. Design of the Current Controller for CC Charge
Fig. 13 shows the design process of the inner loop for the input current control with Bode plot by using Matlab. As shown in Fig. 12, since the transfer function for the input current is the minimum-phase system with enough phase margins, a controller with 2-pole/1-zero was used to reduce the steady-state error by increasing the DC gain to enhance the dynamic performance of the system by selecting a suitable crossover frequency.
The equation (10) and Table III show the transfer function of the inner control-loop and its parameter values. A crossover frequency was selected at 6kHz, one-fifth of the switching frequency. It can be seen in the Fig. 9 that the DC gain of the closed-loop transfer function has been largely increased, thereby reducing the steady-state error.
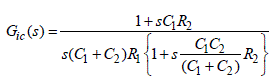image
Also, the slope of the closed-loop transfer function at crossover frequency is -20dB/dec. Upon compensation, the phase margin is 60 degrees and the gain margin is more than 50dB, both of which indicate that the controller has been designed appropriately.

B. Design of the Voltage Controller for CV Charge
As abovementioned, a voltage control transfer function is a non-minimum phase system having additional phase delays due to the right-half-plane (RHP) zeroes. Accordingly, a crossover frequency is limited by a third of the RHP zero frequency in order to guarantee the stable operation of the converter and thus the dynamic characteristics of the converter becomes poor. However, it is not important because the dynamic characteristic of the converter is not a critical factor for the battery charge application.
Therefore, 1-pole/1-zero controller is used for the voltage controller to increase the DC gain of the voltage control loop in the low frequency regime since it has a pole at the origin. The equation (11) and Table IV are the transfer function and parameter values of the voltage controller. Fig. 9 shows the design process of the outer loop for the output voltage control with Bode plot by using Matlab. The crossover frequency of the closed loop transfer function is 15Hz, onesixths of the frequency of the left half plane zero. As can be seen in the Fig. 14, the phase margin and gain margin of the closed loop transfer function is 80 degree and 30dB respectively, both of which indicate that the controller has been designed to guarantee the stable operation of the charge system.
image

EXPERIMENT AND CONSIDERATION
To verify the validity of the proposed charge algorithm, an experiment was conducted. The microprocessor used in this experiment is TMS320F28335, Digital Signal Processor by TI.
Fig. 15 shows the flow chart of the control algorithm implemented in the DSP. To detect current, LA55-P, current transducer from LEM, was used, while voltage was detected by a differential amplifier circuit due to the inverse polarity of the output voltage. Also, in order to convert the analogue controller designed above into digital form, bilinear transformation was used and the results are shown in (12) and (13).
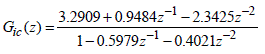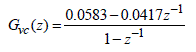image
image
A data logging system was implemented by using LabVIEW software and PCI-6154 data acquisition board from National Instruments to record the charge profile. In the constant current mode charge, the battery needs to be charged with 1C-rate current, 4A in this case. The maximum charge voltage for the battery is 12.6V and the minimum discharge voltage is 9V. The charge profile obtained during which a lithium polymer battery was charged from a small PEM fuel cell stack by using the developed charger is shown in the Fig. 16. During the CC mode charge, output current of the converter is controlled at 4A. The battery voltage at this time gradually increases until it reaches to the output voltage reference (12.6V, maximum charge voltage) as shown in the Fig. 16. When the battery voltage reaches to the reference voltage, the controller automatically transfers its charge mode to CV mode, in which the charge current is exponentially reduced, while its voltage is consistently maintained at 12.6V.
As was seen in the experimental results, CC and CV mode charge was performed successfully, thereby verifying the stable operation of the charger and its control algorithm. Fig. 17 shows the waveforms of the input current to the converter from the PEM fuel cell stack and the charge current to the battery in the CC mode, respectively. As shown in the Figure 17, input current has 30 kHz switching ripple and the magnitude of the battery current ripple is approximately 100mA, which is less than 3% ripple ratio, and it satisfies the current ripple requirements for the battery.

CONCLUSION
In this study, a portable fuel cell charger was designed by using a small PEM fuel cell stack and a Cuk converter. To charge the battery in CC/CV modes, current and voltage were controlled by a single control loop, simplifying the software, and its feasibility was verified through the experiments. The developed charger can be used for the boost charge application using fuel cells.

ACKNOWLEDGMENT
This work was supported by the Human Resources Development program No.20124030200070 of the Korea Institute of Energy Technology Evaluation and Planning(KETEP) grant funded by the Korea government Ministry of Trade, Industry and Energy.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 11 Figure 12 Figure 13 Figure 14 Figure 15
Figure 11 Figure 12 Figure 13 Figure 14 Figure 15
Figure 16 Figure 17
Figure 16 Figure 17
 

References
  1. Chen J.-J., Yang F.-C., Lai C.-C., Hwang Y.-S., and Lee R.-G., "A High-Efficiency Multimode Li–Ion Battery Charger With Variable Current Source and Controlling Previous-Stage Supply Voltage," IEEE Trans. Ind. Appl., Vol. 56, No. 7, pp. 2469～2478, 2009
  2. Yang Bo, Lee F.C., Zhang A.J., and Huang G., "LLC Resonant Converter for Front End DC/DC Conversion," in Proc. APEC 2002, Vol. 2, pp. 1108～1112, 2002,
  3. Lee K., Cho Y., Park J., Kim Y., Kim J. and Chang N., "A Fuel-Cell-Battery Hybrid Platform for Portable Embedded Systems," in Proc. 17th IFAC, pp. 2188～2193,2008
  4. Sang-hwaJung, Young-jinWu, Nam-in Kim, "Analogue-digital Switching Combination Low Ripple-High efficiency Li-Ion Battery Charger," 2001 Korea Electric Academic Conference Paper, pp. 2531～2533, 2001
  5. W. Gu, "Small signal modeling for current mode controlled Cuk and SEPIC converters," in Proc. APEC 2005, Vol. 2, March, 2005, pp. 906~910.
  6. Dongyuk Mechatronics Lab, Secondary Power Cell and Battery Charging Device Deisgn, International Techno Infomration Lab, 2005.
  7. Hwa-young Won, Soo-yongChae, Sun-chanHong, "Interpretation of Charging and Discharging System for Lithium Cells by Average State Space," Electric Power Conference Paper, 14th Edition, 5th Version, pp. 387~396, 2009.
  8. Erickson Warren, and MaksimovicDragan, Fundamentals of Power Electronics 2nd ed., Kluwer Academic, 2001.
  9. RiawanD.C., and NayarC.V., "Analysis and design of a solar charge controller using cuk converter," in Proc. AUPEC 2007, pp. 1~6, 2007.
  10. KittipeerachonK., and BunlaksananusornC., "Feedback compensation design for switched mode power supplies with a right-half plane (RHP) zero," in Proc. PEMD 2004, Vol. 1, pp. 236～241, 2004.
  11. Diaz D., Garcia O., Oliver J.A., Alou P., and CobosJ.A., "Analysis and design considerations for the right half -plane zero cancellation on a boost derived dc/dc converter," in Proc. PESC 2008, pp. 3825~3828, 2008
  12. Huang X., Wang X., NergaardT., Lai J.,Xu X. and Zhu L., "Parasitic ringing and design issues of digitally controlled high power interleaved boost converters," IEEE Trans. Power Electron., Vol. 19, No. 5, pp. 1341~1352, 2004.
  13. Han-ulPark, Eun-sooKim, Su-sukKim, Joong-ho Song, "Insulation Inverse-SPIC's Modeling and Control Characteristics," Electric Power Conference Paper, 13th Edition, 1st Version, pp. 1~8, 2008.