Control Techniques for Single Phase Inverter
to Interface Renewable Energy Sources with
the Micro grid

V Senthil Kumar; S Arun Jees; Dr.V Gomathi

Control Techniques for Single Phase Inverter to Interface Renewable Energy Sources with the Micro grid

V Senthil Kumar¹, S Arun Jees ² , Dr.V Gomathi³

PG Student, Power Systems Engg, Department of EEE, CEG, Anna university, Chennai, India¹
Research Scholar, Power Systems Engg, Department of EEE, CEG, Anna university, Chennai, India²
Assistant Professor, Power Systems Engg, Department of EEE, CEG, Anna university, Chennai, India³

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, a novel current control technique is proposed to control both active and reactive power flow from a micro grid system fed by a renewable energy source through a single phase parallel-connected inverter. The parallel connected inverter ensures active and reactive power flow from grid with low total harmonic distortion even in the presence of non linear load. A p-q theory based approach is used to find the reference current of the parallel connected inverter to ensure desired operating conditions at the grid terminal. The proposed current controller is simple to implement and gives superior performance over conventional current controllers, such as rotating frame proportional-integral controller or stationary frame proportional resonant controller. The stability of the proposed controller is ensured by direct Lyapunov method. Detailed simulation are carried out in MATLAB/SIMULINK and the results are presented to show the efficacy of the proposed current control scheme along with the proposed nonlinear controller to control the active and reactive power flow in a single-phase microgrid under different operating conditions.

Keywords

Lyapunov-function-based controller, parallel-connected current-controlled voltage source inverter (CCVSI), p-q theory based current calculator.

INTRODUCTION

MICROGRID research is becoming more and more popular due to a need of economic usage of electric power. Nowadays, renewable energy sources are heavily used to reduce the generation of electricity using natural coal and other fossil fuels. Electrical power systems are getting more and more stressed due to the increase in power demand, limitation on power delivery capability of the grid, complications in building new transmission and distribution lines, and leading to blackouts [1]. Developments of power electronic converters along with its sophisticated high performance controllers make it possible to integrate different types of renewable energy sources to the Microgrid [2]-[6]. Mostly it can be seen that extensive research is undertaken to connect renewable energy sources to three phase grids using three phase pulse width modulation (PWM) inverters.

In case of medium power Microgrid application, single phase inverters are gaining popularity. In a typical residential application, the renewable energy is used to reduce the load power demand from the Microgrid. These grid connected inverters are extensively used in three phase Microgrid to have active, reactive power control as well as used as active filter to minimize the harmonic contents in the grid current (controlling the harmonic power) drawn by the load [7]-[9]. In order to facilitate active and reactive power control of the grid, in three phase inverters current tracking is carried out using Proportional Resonant (PR) controllers implemented in synchronously rotating “d-q” frame. The grid current harmonics are reduced by using proportional-integral (PI) and multiple PR controller implemented in synchronously rotating “d-q” frame. Similar type of current control is also carried out by using repetitive controller as well as iterative learning controller [14]. All these current controls are implemented in the synchronously rotating “d-q” frame.

In this paper, a Lyapunov-function-based current tracking controller is proposed for the single –phase microgrid-connected renewable energy sources through the inverter [11]. The proposed controller is easier to implement in comparison with other type of controllers. It is directly implemented in real phase domain and is independent of the grid fundamental frequency. The proposed controller is shown to have fast convergence of the tracking error. The stability of the controller is derived by using direct Lyapunov method.

A typical structure of multi bus Microgrid configuration considered is shown in the Fig.1. The Microgrid comprises of three paralleled distributed generation (DG) systems, viz., DG1, DG2, and DG3.

DG1 comprises renewable energy sources along with associated power electronic energy extractor and interfaced to the local bus using a parallel connected inverter topology. [2]-[3] At the dc link of the inverter, energy storage element (such as battery, etc.) is also connected. In the local bus, some critical loads are connected. The focus of this project work lies in discussing the control of the parallel-connected inverter inside the DG1. Under normal mode of operation, the microgrid is connected to the utility grid at the PCC through a static transfer switch (STS). In this mode, inside DG1, most of the extracted renewable energy is stored in the battery, and the critical loads draw active power from the common bus via local bus. But, if needed, certain amount of extracted or stored energy is also fed to the common bus via local bus to reduce the active power consumption from the local bus.

In the case of islanded condition, when the Microgrid is isolated from the main utility grid by means of STS switch, the power demand of all the DG systems is changed and each of the DG systems should immediately follow the changed power demand to stabilize the voltage in the common bus in the Microgrid. In this paper, a control technique is proposed and validated by experimental studies for the parallel inverter inside DG1 [10]. The current reference for the inverter is obtained by subtracting the desired grid current from the measured load current. In case there is a voltage change in the local bus, the proposed control method is capable of maintaining the required power demand by automatically adjusting the current of the CCVSI. All the characteristics of the DG1 can also be achieved in case of utility grid-connected mode. In this mode, the proposed control technique also eliminates the need of external power factor correction (PFC) circuit as the proposed current control method makes the single inverter to do both power control and local grid current THD control.

DESCRIPTION OF THE INVERTER CONFIGURATION AND ITS CONTROL

A. DESCRIPTION OF THE INVERTER ASSEMBLY

The inverter power circuit is preceded by a set of renewable energy extracting apparatus and the renewable energy extractor is directly connected to the power electronic converter (PEC). PEC is a typical dc/dc converter if the renewable energy extractor is a photovoltaic (PV) panel or a fuel-cell-based system, and a typical ac/dc converter if the renewable energy extractor is a permanent magnet or induction-machine-based wind turbine.

The PEC output is connected to the dc link of the PWM voltage source inverter (VSI). At the dc link of the PWM VSI, an energy storage element, battery, is also connected in parallel with the PEC converter output. As depicted in Fig.2. , the PWM VSI is directly connected in parallel with the Microgrid, operating in current controlled VSI mode.

The load is directly connected to the Microgrid. The power electronic converter is operated in such a way that the renewable energy source operates in maximum power point (MPP) and MPP active power PMPP is extracted from the renewable energy source [16]-[17].

B. REFERENCE CURRENT OF THE INVERTER

Assuming that the PEC converter is extracting maximum power (at maximum point operation) from the renewable energy source and the storage element battery is operating properly, the inverter dc link can be modelled as a dc power source. The local bus voltage, where the targeted load and the renewable energy source-based inverter are connected, is called the grid voltage vg. The load is connected to the grid voltage vg and the parallel CCVSI can be regarded as the shunt active current ic compensator

If the required amount of active and reactive power flow from the grid is Pg and Qg, respectively, then the reference grid current magnitude can be found by applying p–q theory [15]. To apply the p–q theory, the concept of real and imaginary axes is introduced as shown in Fig.3 (b). The real axis grid voltage is vgr = vg, and the real axis grid current reference is igr= . The corresponding imaginary axis grid voltage and the imaginary axis grid current references are vgi and igi, respectively. If the instantaneous value of a quantity in real axis is known, the instantaneous value of the corresponding quantity in the imaginary axis can be estimated by passing the real axis quantity value through the Hilbert transform (providing 90Ãâ¹ÃÅ¡ phase lead to all the frequencies).

The Hilbert transform operation is approximated as passing the real axis quantity through the all pass filter H(s) = (1 – Ts) / (1 + Ts), where T = 1/ω and ω is the fundamental power frequency in radians per second. By using this technique, vgi is estimated from the instantaneous measurement of vgr . Therefore, in terms of time-domain convolution, vgi(t) = h(t) * vgr(t). Using p–q theory [15]-[17], the instantaneous active and reactive power flow balance equation at the grid can be written as follows:

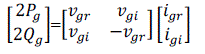The multiple of “2” in the left side of (1) is due to the fact that, to use the space vector concept in power calculations, the imaginary axis is introduced, therefore, the total power shown in the left side of (1) is taking care of the total power handled by both the real and imaginary axes. By inverting the matrix in (1), the igr and igi can be solved. The real grid current reference can be calculated as follows:

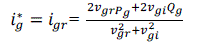If Kirchhoff’s Current Law (KCL) is applied at the PCC terminal, the reference current for the CCVSI is found by measuring the load current iL , as given by

Therefore, by sensing the instantaneous load current iL and the grid voltage vg , the instantaneous value of the CCVSI current reference ∗ can be found using (2) and (3), depending on the Microgrid active as well as reactive power flow requirements Pg and Qg , respectively, as shown in Fig.4. In the Fig.4. the inverter current reference is produced as the comparator result, and it is obtained by comparing the load current with the reference current of the grid.. The active and reactive power values are given as per the required output power value.

DESIGN OF NON LINEAR CONTROLLER BASED ON LYAPUNOV FUNCTION

A.MODELLING OF THE CCVSI SYSTEM

CCVSI current reference ∗ can have any type of periodic shape depending on the load. In order to ensure proper power flow, a fast current tracking controller is needed. The current tracking system of the CCVSI can be modelled as a first-order system [11]-[14], as shown in Fig.5. Neglecting the switching-frequency-related harmonic voltages, the VSI is modelled as a dependent voltage source vinv = Vdc × vc , where vc is the control signal of the sine PWM process.

The dynamic equation of the CCVSI current ic can be written as follows:

To analyze the system from control point of view, the state of the system is chosen as: x = ic , control input u = vc , disturbance input d = −(1/L)vg , state function f(x) = −(R/L)ic , and the input function b(x) = Vdc/L. Therefore, the state equation of the system can be written as follows:

However, the considered model of the sine-pulse-width modulation (SPWM) inverter is simple and it does not consider any unpredictable nonlinear periodic disturbances dup (one such possible source is the blanking time in the inverter driver circuit). In actual circuit, these nonlinear periodic disturbances play important roles. In practical cases, the disturbance term d in (5) consists of not only grid voltage disturbance − (1/L) vg , but also the unpredictable nonlinear disturbances as follows :

B.DETERMINING THE LYAPUNOV-FUNCTION BASED CONTROL LAW TO ENSURE CURRENT CONTROL

It is needed to generate the control input u (t) so that x = ic tracks the reference value xd = . The dynamic tracking error can be written as e = xd − x. It is required to find out a control input u(t) such that tracking error e(t) asymptotically converges to zero. Lyapunov direct method is used to find out the control input u(t) for this specific application.

The Lyapunov function is taken as follows:

According to the property of Lyapunov function, V > 0 for all the conditions except e = 0 in this case. Thus, the selected V can be mentioned to be a positive definite function. Differentiating (7) with time, we have

Substituting (5) into (8), the resulting equation becomes as follows:

In order to make the control input u effective enough to force the tracking error e to converge to zero [10]- [14], the first derivative of the chosen Lyapunov function needs to be negative definite. For the present case, the first time derivative of the Lyapunov function is chosen as follows;

where, λ is a strictly positive number. Comparing (9) and (10), the relationship can be written as follows:

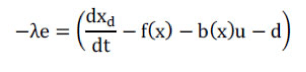From this equation control input

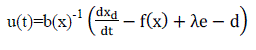C.ESTIMATION OF THE DISTURBANCE TERM “d” TO FACILITATE THE CONTROL ACTION

The control law shown in (11) can be divided into two parts as follows:

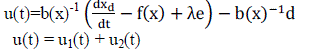Equation (12) shows that the term u2(t)=( −b(x) d) is dependent on the grid voltage as well as other unpredictable periodic disturbance terms, as shown in (6). In this case, part of d dependent on vg can be obtained by sensing the microgrid voltage vg using voltage sensor, but the unpredictable part dup, as shown in (6), cannot be measured but can be estimated if the proper nonlinear model of the inverter is known. Irrespective of all these, d cannot be estimated properly due to the phase lag associated with the voltage sensor and model inaccuracy of the inverter. Considering this, the estimated value of disturbance term is different from actual value d, and the control input can be rewritten as follows:

Plugging-in (13) in (8), the equation can be modified as follows:

Thus the tracking error e converges to a value e1b if ≠ d as follows

Under these circumstances, if the disturbance d is estimated using an SRC based on the residual tacking error, then, at steady state, = d and current tracking becomes perfect with e = 0. Therefore, the second part of the control signal in (12) is denoted as u2 (t) = uSRC(t) and the first part of the control signal is called u1 (t) = uLf (t). For the microgrid conditions, the inverter unpredictable nonlinearities as well as grid voltage do not change very often, therefore the slow dynamics of the SRC control law uSRC(t) is dominated by the fast dynamics of feedback Lyapunovfunction- based control law uLf (t). In this condition, if there is a sudden change in current reference , the actual CCVSI current ic is observed to follow almost in no time with the Lyapunov-function-based controller unlike the slow condition in the case of SRC.

D. EFFECT OF PARAMETER UNCERTAINTY ON THE CONVERGENCE

It is considered that the disturbance term “d” in (11) is estimated. However, functions f(x) and b(x) are dependent on system parameters such as inductance L and resistance R. The parameters L and R of the choke coil cannot be accurately determined. As there is uncertainty in the estimation of the system parameters, the estimated value of the system parameters are (x) and (x) instead of actual f(x) and b(x) respectively. Under such circumstances, the control input shown in (11) is modified as follows:

Plugging in (16) in (9), the resulting equation can be found out as follows:

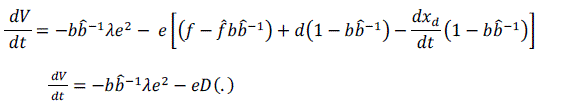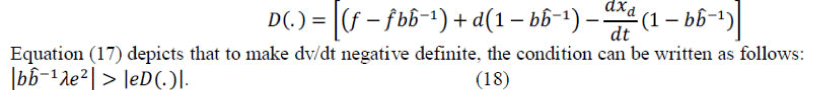Equation (18) shows that the quantity λ needs to be big enough to satisfy (18) within the appreciable range. If it is designed such that the absolute value of error converges to error bound eb, which is closer to 0, the value of λ needs to follow the condition.

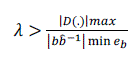E.DESIGN OF THE LYAPUNOV-FUNCTION BASED CONTROL LAW

The parameters used for testing the proposed control system are: the dc link voltage Vdc = 100 V, the maximum value of grid voltage disturbance |Vg |max = 50 ×√2 = 70.7 V, choke coil inductance L = 6mH, resistance R =1Ω, and inductance and resistance uncertainties are considered to be 10% in each case. For the simplicity of design, the peak value of the tracked current is considered to be |ic |peak = 6A, and the maximum rate of change present in the reference current is considered to be the product of peak current |ic |peak with maximum frequency component present in the reference current ωes . In this case, ωes = 1 kHz assumed. This condition is further ensured by putting an antialias filter of cut-off frequency around 1 kHz in the feedback path. Considering these conditions, the maximum value of D(.) [Shown in (17)] can be calculated as follows:

Considering absolute error bound eb = 0.01 and using (19), the controller parameter is found to be as follows:

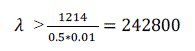F.IMPLEMENTATION OF THE LYAPUNOV BASED CONTROL SYSTEM

The SPWM switching frequency is taken as fs = 10 kHz. The first time derivative term in ufb is replaced by its backward approximation rule. Considering (4), (5), and (13), the Lyapunov-function-based control law for PWM (control input) at kth sampling instant can be written as follows:

where Ts = 1/fsample is the sampling time of the control system. The block diagram of the implemented reference current calculator followed by the current controller is shown in Fig.3. The output of the controller is clamped by a saturation block in actual experiment. This always ensures linear range of operation of SPWM process.

RESULTS OF IMPLEMENTATION OF THE CONTROL STRATEGY

Lyapunov function based control strategy was implemented in order to control the single phase parallel connected converter, through which the active power and the reactive power from the microgrid can be controlled.

A. DETAILS OF THE POWER CIRCUIT USED IN THE SIMULATION

The proposed controller is validated by extensive testing on a developed prototype. The prototype is made out of a microgrid voltage Vg=50 Vrms and the dc link voltage level of the CCVSI is taken to be Vdc=100 V. The load is taken to be a resistive, capacitive assembly. In this control topology, the single parallel inverters is not only controlling the active and reactive power flow from the grid, but also compensating for the non-linear current drawn by the load from the grid terminal. Therefore, inverter current consists of both sinusoidal power current and the inverse non linear load current. The non linear load current has substantial di/dt due to the capacitor termination at the dc side of the rectifier load. To take care of the substantial voltage drop in choke coil of the CCVSI, the dc link voltage is taken as more than the required value. This higher dc link voltage also ensures better transient of the proposed current controller because of the inverter PWM phenomena.

The parameters of the power circuit are also given in the Table .1. At the specified grid voltage level (50 Vrms), the load draws active power PL=35 W with unknown reactive as well as harmonic powers.

Normally SPWM technique is used in order to give the pulse to the switching devices. Here in the power circuit single phase full bridge inverter is used and hence 4 IGBT is being used. For the alternate IGBT same gating pulse was given, thus the inverter produces the output and that is connected to the microgrid voltage Vg. The control strategy which was discussed in the Fig.7. is implemented in the power circuit which was considered for the simulation purpose. The simulation circuit after the implementation of the Lyapunov function based current controller is shown in Fig.8.

The proposed controller is validated by extensive testing on a developed prototype. The prototype is made out of a micro-grid voltage Vg=50 V rms and the dc-link voltage level of the CCVSI is taken to be Vdc=100 V. The Lyapunov function based controller output (Ulf) is depicted in Fig.9. SPWM stands for sinusoidal pulse width modulation. SPWM requires two signals. Lyapunov output (Ulf) is the first signal and the other signal is triangular wave which is said to be carrier signal. These two signals werecompared by using the relational operator block, in which the sine wave is lesser than the triangular wave means the gate signal will be produced.

At first the active and reactive power command to the grid is given to be pg=0 W & qg=0 var. From this we can reveal that the grid current, ig = 0 and the load current is contributed by CCVSI current ic. The experimental results are Inverter Voltage, Inverter Current, Load Current, Grid Current, Grid Voltage when Power Command pg=0 & qg=0 is shown in Fig.10. Active and reactive power flow from the grid with low-current THD is shown in Fig.11. This is obtained when the power command is pg=10W & qg=0var.

The control system is further tested by changing the grid power command to pg=30 W & qg=0 var. The inverter voltage, inverter current, Load current, Grid current, Grid voltage for the above grid power command is shown in Fig.12. The proposed controller controls the CCVSI current ic. ie, the grid current ig becomes sinusoidal with peak amplitude of 0.82 A and rms ig =0.6 A. The grid current is inphase with the grid voltage. Inverter current changes from load current when the active power command (Pg) to the grid changes from 0 to 30.

CONCLUSION

A new current control strategy for the parallel-connected inverter connected to microgrid is proposed.The current reference calculator uses the “p–q” theory in place of the conventional one step ahead integrator block making the reference cur-rent estimation faster. The proposed Lyapunov-function-based nonlinear control is simple to implement as well as provides superior performance over conventional controllers such as ro-tating frame PI controller. The control law is also simple to implement in digital domain over the other established rotating frame controllers. The experimental results show that the proposed controller along with the “p–q” current calculator is capable of controlling the active and reactive power flow from the microgrid in a decoupled manner along with controlling the THD of the grid current. This power control property facilitates the efficient usage of renewable energy in a microgrid.

Tables at a glance

Table 1

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

Figure 5	Figure 6	Figure 7	Figure 8

Figure 9	Figure 10	Figure 11	Figure 12

References

Xue, J. Deng, and S. Ma, “Power flow control of a distributed generation unit in micro-grid,” in Proc. IEEE Int. Power Electron. Motion Control Conf., 2009, pp. 2122–2125.
J. M. Carrasco, L. G. Franquelo, J. T. Bialasiewicz, E. G. Galvan, R. C. P. Guisado, M. A. M. Prats, J. I. Leon, and N. M. Alfonso, “Powerelectronic systems for the grid integration of renewable energy sources: A survey,” IEEE Trans. Ind. Electron., vol. 33, no. 4, pp. 1002–1016, Aug. 2006.
F. Blaabjerg, R. Teodorescu, M. Liserre, and A. V. Timbus, “Overview of control and grid synchronization for distributed power generation sys-tems,” IEEE Trans. Ind. Electron., vol. 53, no. 5, pp. 1398–1409, Oct. 2006.
J. M. Guerrero, J. Matas, L. G. de Vicuna, M. Castilla, and J. Miret, “Decentralized control for parallel operation of distributed generation inverters using resistive output impedence,” IEEE Trans. Ind. Electron., vol. 54, no. 2, pp. 994–1004, Apr. 2007.
J. C. Vasquez, J. M. Guerrero, A. Luna, P. Rodriquez, and R. Teodorescu, “Adaptive droop control applied to voltage-source inverters operating in grid-connected and islanded modes,” IEEE Trans. Ind. Electron., vol. 56, no. 10, pp. 4088–4096, Oct. 2009.
R. H. Lasseter and P. Paigi, “Microgrid: A conceptual solution,” in Proc. Annul IEEE Power Electron. Spec. Conf., 2004, pp. 4285– 4290.
N. Pogaku, M. Prodanovic, and T. C. Green, “Modeling, analysis and testing of autonomous operation of an inverter-based microgrid,” IEEE Trans. Power Electron., vol. 22, no. 2, pp. 613–625, Mar. 2007.
S. B. Kjaer, J. K. pedersen, and F. Blaabjerg, “A review of single-phase grid-connected inverters for photovoltaic modules,” IEEE Trans. Ind. Appl., vol. 41, no. 5, pp. 1291–1306, Sep. 2005.
F. Carastro, M. Sumner, and P. Zanchetta, “Mitigation of voltage dips and voltage harmonics within a micro-grid, using a single shunt active filter with energy storage,” in Conf. Rec. IEEE Annu. Conf. Ind. Electron. (IECON), 2006, pp. 2546–2549.
A. V. Timbus, R. Teodorescu, F. Blaabjerg, M. Liserre, and P. Rodriguez,“Linear and nonlinear control of distributed power generation systems,” in Proc. IEEE Conf. Rec. Ind. Appl. Soc. (IAS) Annu. Meet., 2006, pp. 1015– 1023.
S. Dasgupta, S. K. Sahoo, and S. K. Panda, “A novel current control scheme using Lyapunov function to control the active and reactive power flow in a single phase hybrid PV inverter system connected to the grid,” in Proc. IEEE Conf. Rec. Int. Power Electron. Conf. (IPEC), 2010, pp. 1701– 1708.
X. H. Wu, S. K. Panda, and J. X. Xu, “DC link voltage and supply-side current harmonics minimization of three phase PWM boost rectifiers usingfrequencydomainbasedrepetitivecurrentcontrollers,” IEEETrans. Power Electron., vol. 23, no. 4, pp. 1987–1997, Jul. 2008.
S. Fukuda and T. Yoda, “A novel current-tracking method for active filters based on a sinusoidal internal model,” IEEE Trans. Ind. Appl., vol. 37, no. 3, pp. 888–895, May/Jun. 2001.
S. Dasgupta, S. Sahoo, S. Panda, and G. A. J. Amaratunga, “Single-phase inverter control techniques for interfacing renewable energy sources with micro-grid—Part II: Series connected inverter topology to mitigate voltage related problems along with active power flow control,” IEEE Trans. Power Electron., vol. 26, no. 3, pp. 1–15, 2011.
M. Saitou and T. Shimizu, “Generalized theory of instantaneous active and reactive powers in single-phase circuits based on Hilbert transform,” in Proc. Conf. Rec. Power Electron. Spec. Conf. (PESC), 2002, vol. 3, pp. 1419–1424.
C. Rodriguez and G. A. J. Amaratunga, “Analytic solution to the photo-voltaic maximum power point problem,” IEEE Trans. Circuits Syst. I: Regular Papers, vol. 54, no. 9, pp. 2054–2060, Sep. 2007.
E. Koutroulis and K. Kalaitzakis, “Design of a maximum power track-ing system for wind-energy-conversion applications,” IEEE Trans. Ind. Electron., vol. 53, no. 2, pp. 486–494, Apr. 2006.