COST OPTIMIZATION OF STAND ALONE
HYBRID POWER GENERATION SYSTEM
USING PSO

G. Naveen Ram; J. Devi Shree; A. Kiruthiga

COST OPTIMIZATION OF STAND ALONE HYBRID POWER GENERATION SYSTEM USING PSO

G. Naveen Ram¹, J. Devi Shree², A. Kiruthiga³

Assistant Professor, Dept. of EEE, Kalaivani College of Technology, Coimbatore, Tamil Nadu, India¹
Assistant Professor (Sr. Grade), Dept. of EEE, Coimbatore Institute of Technology, Coimbatore, Tamil Nadu, India ²
Assistant Professor, Dept. of EEE, Sasurie Academy of Engineering, Coimbatore, Tamil Nadu, India³

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The diminishing fossil-fuel reserve and increasing demand of the world’s population makes it mandatory to look forward to new ways of energy generation. With the advancement in technology and innovations we are able to solve our energy crises and the best answer is energy from renewable sources. Wind turbine generators and PV panels have their own merits for not contributing pollution in the environment but they require high capital and installation costs. This paper deals with providing optimal design of stand-alone hybrid power generation plant comprising of wind turbine generators, PV panels and storage batteries connected to a diesel generator for additional needs. The main objective of the design criteria is to minimize the total cost which includes initial, operational and maintenance cost. For achieving optimal design conditions for this hybrid system, metaheuristics particle swarm optimization is adopted. To illustrate the design procedure the simulation results of the proposed method is discussed.

Keywords

Energy crisis, Hybrid wind–photovoltaic system, Cost minimization, Particle swarm optimization.

INTRODUCTION

Global warming and climatic shift has become a major concern now-a-days. Because of this, most of the countries have begun to turn their attention towards the clean green renewable energy sources. This is currently widely used which poses a bright future for the worlds energy needs. Many researchers have started to focus on this area as these are sustainable and convenient alternatives. The design of hybrid solar-wind power systems (HSWPS) has received considerable attention in the last decade.

Main reason for adopting these two energies in particular has two main reasons. Firstly, WTG will not bring any adverse effect on the environment .Secondly PV arrays are durable, produce no emission and demand minimal maintenance to operate. But the main problems in these resources are they are time dependent. Solar energy is not available during night time and cloudy days which can be unpredictable. Similarly, wind energy also will not be available throughout the year. As a result of this nature of the energy sources, power fluctuations will be incurred since both power sources are highly dependent on weather condition. To minimize these effects on the power system, energy storage technologies such as storage batteries can be employed. Storage batteries will absorb surplus power and supply the deficit power in various demanding conditions of power system.

Here, we are going to discuss about implementation of an approach to formulate various design criteria’s for the hybrid power system connected to the conventional generator by taking into account the economical aspect of the system as an objective function. This helps the designer to study the system thoroughly, to make necessary changes to obtain the perfect alternative suggestion for the operation of this system. Due to high complexity of the design parameters, metaheuristic approach of particle swarm optimization (PSO) is adopted to assist in the decision-making support. This optimization technique has turned out to be an outstanding optimizer due to its ability to solve difficult optimization problem as well as its exceptional convergence performance.

PROPOSED HYBRID POWER GENERATION SYSTEM

The block diagram of the proposed integrated wind, PV and storage batteries generating system is shown in Fig 1. This configuration can be used for the study of stand-alone systems as well as network-connected systems. For the standalone system, if the demand is greater than the sum of generation and storage, then power must be supplied by the backup generator. For the network-connected configuration, the backup generator is not needed. Furthermore, if the total generated power is greater than the demand, and the storage is full, then the excess generation is dumped to an external voltage-controlled resistive load. The purpose of incorporating a dumped load into the system is to preserve the stability of the system frequency and voltage. If the excess energy cannot be dissipated usefully, then it must be disposed as heat. These power sources have different impacts on cost, environment, and reliability. In a hybrid generation system, they are integrated together and complement one another in order to serve the load while satisfying certain economic, environmental, and reliability criteria.

OBJECTIVE FUNCTION

The objective function of this research is to develop a stand-alone hybrid generation system, which is appropriately designed in terms of all economic aspects and measures subject to the operational constraints of the system. In other words to minimize the total cost. The total cost ($/year) includes initial cost, operational and maintenance (OM) cost for each type of power source, and the salvage value of each equipment which should be deducted.

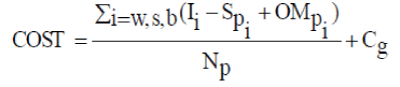where w, s, b indicate the wind power, solar power, and battery storage, respectively; are the initial cost, present worth of salvage value, and present worth of operation and maintenance cost (OM) for equipment i , respectively; NP (year) is the lifespan of the project; and Cg is the annual cost of generating power from backup generator.

A. For Wind Turbine Generators

Initial cost is

Iw = αwAw

α w ($/m2) is the initial cost of WTGs.

Present total salvage value is

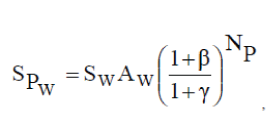Sw ($/m2) is the salvage value of WTGs per square meter,

β Inflation rate, γ Interest rate.

Present worth of OM

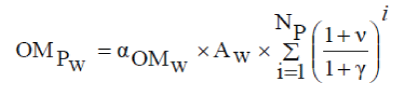α ($/m2/year) is the yearly OM cost per unit area,

is the escalation rate.

B. For PV Panels

Initial cost is

Is = αsAs

($/m2 ) is the initial cost.

Present total salvage value is

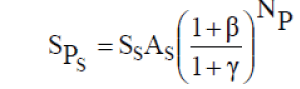($/m2 ) is the salvage value of PVs per square meter.

Present worth of OM

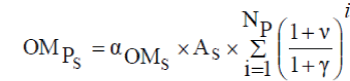α ($/m2/year) is the yearly OM cost per unit area,

is the escalation rate.

C. For Storage Batteries

Initial cost is

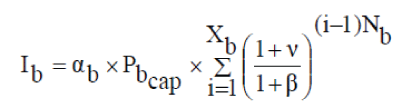N is the lifespan of SB,

X is the number of times to purchase the batteries during the project lifespan,

Np is the salvage value of Storage batteries and it is ignored in this calculation.

Present Total OM cost

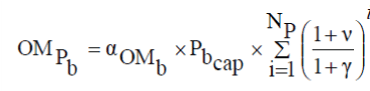αOM ($/kWh/year) is the yearly OM cost per kilo watt-hour.

D. For the backup generator

Annual cost of generating power

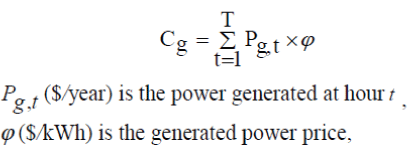T (8760 h) is the operational duration under consideration

CONSTRAINT

The total power generated from the hybrid system should meet the power demand at all time, t with some reliability. This can be mathematically expressed as

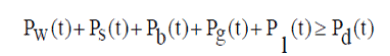Pw - Wind power, Ps - Solar power, Pb - Discharged battery power, Pg - Power bought from grid, Pl (t) – Transmission losses, Pd - Total load demand.

VARIBLE BOUNDS

PARTICLE SWARM OPTIMIZATION

The PSO algorithm works by simultaneously maintaining several candidate solutions in the search space. During each iteration of the algorithm, each candidate solution is evaluated by the objective function being optimized, determining the fitness of that solution. The PSO algorithm consists of three steps, which are repeated until some stopping condition is met,

1. Evaluate the fitness of each particle

2. Update individual and global best fitness and positions

3. Update velocity and position of each particle

After every iteration, each particle is updated by following two "best" values. The first one is the best solution (fitness) it has achieved so far. The fitness value is also stored. This value is called “pbest”. Another "best" value that is tracked by the particle swarm optimizer is the best value obtained so far by any particle in the population. This best value is a global best and called “gbest”. After finding the two best values, the particle updates its velocity and positions.

The velocity of each particle in the swarm is updated using the following equation

Once the velocity for each particle is calculated, each particle’s position is updated by applying the new velocity to the particle’s previous position

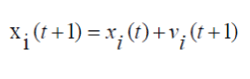A. Algorithm

The computational procedure of the proposed method is as follows

Step 1: Specify the lower and upper bounds of WTG-swept area, area of PV panels, number of batteries, and other predetermined parameters.

Step 2: Initialize the speed and position of each particle by randomly generating a particle population.

Step 3: Based on the method of pareto dominance position of each particle, Diin the population is estimated.

Step 4: The non-dominated solutions estimated in the previous step is stored in the archives.

Step 5: Another archive is created for storing the memory details which contains information about initialization of each particle’s personal best, pbest.

Step 6: Increase the iteration number by one.

Step 7: Evaluate the fitness values according the fitness function; in this paper, the fitness value is defined by cost function and can be calculated. According the fitness value, we will decide whether the solution is good or not. Update the personal-best position pbest and the gbest value based on the memory record.

Step 8: Update the member velocity v of each individual Di.

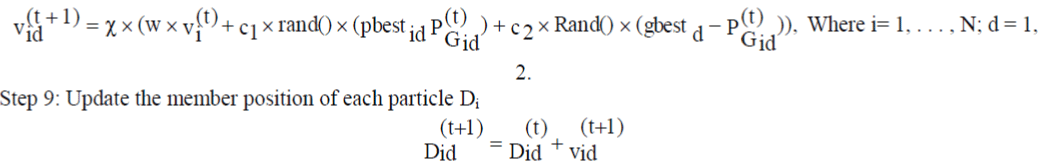For the binary-encoded design variable, update the member position based on the updating rule for discrete variables.

Step 10: Archive that stores the non-dominated solutions should be updated based on the pareto optimality based selection condition.

Step 11: Pbest in the memory is updated based on the dominance of the current value of the individual. If pbest dominates over the current individual keep the memory same without any alteration else update the memory with new pbest value.

Step 12: If a stopping criterion is reached go to next step else go to step 6

Step 13: Print out the set of solutions in the archives as the possible design criteria for the above discussed system.

B. Flow Chart

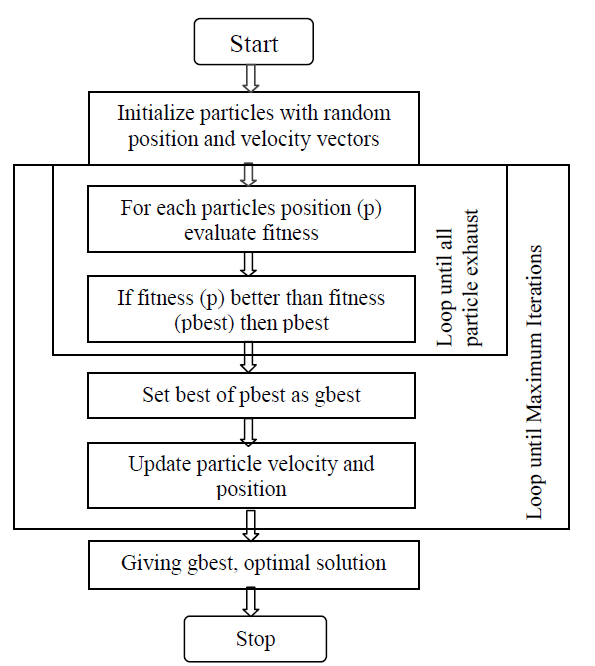C. PSO Parameters

In the simulations, both the population size and archive size are set to 100, and the maximum number of iterations is varied from 100 to 500 to obtain various design criteria’s. The acceleration constants c1 and c2 are chosen as 1. Convergence factor is designed to be in the range of xÃÂÃÂµ (0,1).The inertia weight factor w decreases with the increasing iterations.

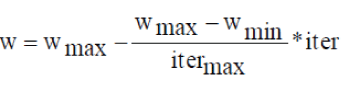Where max iter is the maximum number of iterations and iter is the current number of iterations. The simulation program is coded using Mat lab and executed in a 2.20 GHz Intel dual-core processor with 2GB Ram.

SIMULATION RESULTS

The data used in the simulation program is shown in table 1. The non-dominated solutions based on the pareto dominance was obtained for different design scenarios using the aforementioned procedure and given in table 2.From the simulation results obtained, we find that the non-dominated solutions for cost function considering the design criteria’s varies for different parameters. The user may choose the required system design based on the individual requirement. The different optimization scenarios based on various design parameters are shown in fig 2, fig 3, fig 4,

CONCLUSION

The suggested methodology has considered both accuracy of obtained solutions and computational overhead of the hybrid system. This paper has described techniques for estimating and optimizing the cost of hybrid system using particle swarm optimization. In this proposed method, a hybrid power generation system including wind power, solar power and storage batteries is designed on the basis of cost and their simulation results are discussed for better understanding. The hybrid offers better reliability and lower cost compared to individual renewable sources of energy. The use of renewable energy offers substantial environmental credit when compared to conventional alternatives. The proposed analysis allows the user to study the interaction among economic and operational factors and hence it offers a useful tool for the design and analysis of cost effective hybrid power systems. This work can be further carried out in the future by including the instability in the availability of the renewable energy sources over a period of time.

Figures at a glance


Figure 1	Figure 2	Figure 3


Figure 4	Figure 5	Figure 6

References

R. Chedid, H. Akiki, and S. Rahman, “A decision support technique for the design of hybrid solar-wind power systems,” IEEE Trans. Energy Convers., vol. 13, no. 1, pp. 76–83, Mar. 1998.
J. Kennedy and R. Eberhart, “A discrete binary version of the particle swarm optimization,” in Proc. IEEE Int. Conf. Syst., Man, Cybern., Orlando, FL, 1997, pp. 4104–4108.
D. S. Liu, K. C. Tan, C. K. Goh, andW. K. Ho, “A multiobjective memetic algorithm based on particle swarm optimization,” IEEE Trans. Syst.,Man, Cybern. B, Cybern., vol. 37, no. 1, pp. 42–50, Feb. 2007.
Francois Giraud and Zyiad M. Salameh, “Steady-State Performance of a Grid-Connected Rooftop Hybrid Wind–Photovoltaic Power System with Battery Storage,” IEEE Trans. Energy Conversion, VOL. 16, NO. 1, Mar. 2001.
M. H. Nehrir, C. Wang, K. Strunz, H. Aki, R. Ramakumar, J. Bing, Z. Miao, and Z. Salameh, “A Review of Hybrid Renewable/Alternative Energy Systems for Electric Power Generation: Configurations, Control, and Applications,” IEEE trans. sustainable energy, vol. 2, no. 4, October 2011.
Tomonobu Senjyu, Daisuke Hayashi, Naomitsu Urasaki and Toshihisa Funabashi, “Optimum Configuration for Renewable Generating Systems in Residence Using Genetic Algorithm,” IEEE trans. Energy Conversion, VOL. 21, NO. 2, JUNE 2006.
Riad Chedid, and Saifur Rahman, “Unit Sizing And Control Of Hybrid Wind-Solar Power Systems,” ,” IEEE trans, Energy Conversion, Vol. 12, No. 1, March 1997.
Coello Coello, C. A. and Lechuga, M.S. (2002), “MOPSO: A proposal for multiple objective particle swarm optimization,” Proceedings of Congress on Evolutionary Computation (CEC’2002), Vol. 2, IEEE Press, pp. 1051– 1056.
Kellogg, W., Nehrir, M. H., Venkataramanan, G., and Gerez, V. (1996),”Optimal unit sizing for a hybrid wind/photovoltaic generating system,” Electric Power Systems Research, Vol. 39, pp. 35–38.
H. L. Willis and W. G. Scott,” Distributed Power Generation: Planning and Evaluation,” New York: Marcel Dekker, 2000.