CRITICAL RANKING OF
CONTINGENCIES TO PREVENT
CONGESTION OF POWER FLOW

Pradyumna Kumar Sahoo; Prasanta Kumar Satpathy

CRITICAL RANKING OF CONTINGENCIES TO PREVENT CONGESTION OF POWER FLOW

Pradyumna Kumar Sahoo¹, Prasanta Kumar Satpathy²

Research Scholar, Dept. of EE, ITER, SOA University, Bhubaneswar, Odisha, India ¹
Professor, Dept. of EE, College of Engg and Technology, Bhubaneswar, Odisha, India ²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a scheme for finding the critical ranking of line outage contingencies for preventing power flow congestion in various lines of electric power systems and hence to avoid the risk of voltage instability arising out of such disturbances. The uniqueness of the scheme rests with the determination of the most critical contingency in the system whose status is monitored during each simulation case to ensure voltage stability of the entire network. In order to make a comprehensive analysis of the problem the paper is based on static approaches. The static analysis is based on the conventional Newton-Raphson load flow being supplemented by Continuation Power Flow (CPF) technique. Off-line case studies on IEEE 14-bus and IEEE 30-bus test system are presented

Keywords

Contingency ranking, Power congestion, Voltage collapse, Critical loading margin.

INTRODUCTION

Electric power transmission in a power system is greatly affected by system disturbances such as tripping of equipments/devices and transmission line outages, arising out of disturbances/faults/contingencies. As a result of this, the remaining transmission lines get overstressed in terms of power handling capability, which leads to congestion. If such problems persist and are not timely attended it might lead the whole system towards voltage instability/collapse. Congestion in a power system means overburdening of the existing resources and capacities due to sudden, unprecedented load variations and contingencies as well. As a matter of fact, congestion is not a healthy situation, and if not prevented, it may lead to several chaotic situations and the ultimate threat may be instability and collapse of the system [1, 2]. Therefore, this aspect is drawing a rising attention among the researchers in this field.

However, in this study, the approach is slightly different to tackle the congestion problem. The scheme proposed here takes care of identifying the lines in the distribution network which get over-burdened in the face of congestion subject to a particular contingency condition so that the operator may incorporate alternate provisions to get rid of the congestion problem and hence save the system from voltage collapse.

Voltage collapse in electric power systems is characterized by a monotonically declining voltage at the load buses resulting from disturbances or contingencies together with the inability of the network to meet the reactive power demand at key buses [3]. Besides the long established fact that, voltage collapse is a dynamic phenomenon, a load flow based steady state analysis has become favorable for many researchers [4-6] for its inherent simplistic approach.

The work in this paper has been carried out on an off-line basis that requires examination of all possible contingencies and system conditions. Hence, the study in this paper includes a series of simulation results towards fulfilment of this criterion. The results may include steady state maximum power transfer limit, critical bus identification, postcontingency margin requirement for reactive power and critical switching time of capacitors. In this paper the results obtained for the critical switching time of capacitors has been emphasized. Off-line studies are suitable for operation and planning, hence involve extensive formulation of input databases supporting possible scenarios for their examination. However, the authors are hopeful that with the emergence of present day faster computational setup an on-line application of the proposed scheme may be possible for relatively slower voltage decay events.

This paper is aimed at finding the critical ranking of unforeseen events in form of line outage contingencies for preventing power flow congestion. The results presented in the paper give scope for determining the most critical contingency in the system whose status is monitored during each simulation case to ensure voltage stability of the entire network. In order to make a steady state analysis of the power system, the work in this paper is based on static approach, which makes use of the conventional Newton-Raphson load flow being supplemented by Continuation Power Flow (CPF) technique. Case studies on IEEE 14-bus and IEEE 30-bus test system are presented in the paper.

IDENTIFICATION OF CRITICAL BUSBARS BY STATIC ANALYSIS

Voltage instability is considered as a local load bus problem. The bus, which operates critically, is more likely to initiate voltage instability. In order to assess the criticality of a load bus, a number of credible line outage contingencies are simulated at various loading levels. A line outage case can be modeled in two ways; either by removing the desired line from the system equations or by making the series admittance and shunt capacitance zero. The former is considered in this paper. This analysis is based on static approach. The load model used for this purpose is presented below in equations (1) and (2), which reflects the static behavior of composite load [7, 8].

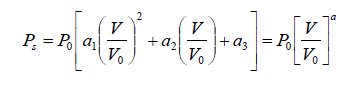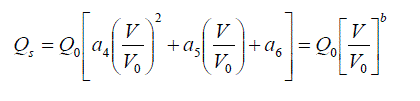A family of Q-V curves as shown in Fig.1 explains the steady state aspects of voltage stability analysis.

In the figure, curve-1 corresponds to the pre-disturbance condition. Each point on this curve represents a specific loading level for which the solutions are obtained from a Newton-Raphson load flow supported with continuation power flow technique [9]. In this work the loads at every bus are increased uniformly. In the same figure, curve-2 represents the post-disturbance condition. This curve clearly illustrates the reduction in reactive power supply following contingencies. However, the demand in the post-contingency steady state still remains a function of the steady state load characteristics. Assuming constant power characteristic of the loads because of ULTC transformer blocking in the post-contingency scenario, the demand curve becomes a vertical line passing through the corresponding operating point, which is shown by curve-3. The corresponding reactive power demand on this curve has a constant value q0. Since the maximum reactive power that can be supplied by the network in the post-contingency period (qmax2) corresponds to the nose of curve-2, a difference between q0 and qmax2 exists, which is otherwise known as the postcontingency requirement of reactive margin or q-departure. In this paper, q-departure is calculated for each load bus and the largest value of which is treated as an indicator for identification of the critical load bus in the network.

CONTINGENCY RANKING BY CONTINUATION POWER FLOW

One major drawback of conventional load flow program is that the Jacobian matrix becomes singular as the system approaches critical loading. By this the solution procedure gets ill conditioned and the results diverge far from intended ones. To overcome this difficulty, a versatile tool called continuation power flow is used. While applying continuation method the conventional load flow equations are reformulated to include another load parameter (λ). The modified set of load flow equations can be written in the form of equation (3), where, is the state variable representing voltage angle and V is the state variable representing voltage magnitude at the system buses. In order to run the continuation power flow the value of (λ) is incremented from zero onwards in suitable steps until the critical point is reached. The solutions for λ=0 refer to base case and those of λ>0 refer to higher loading level above base case.

Continuation Power Flow is based on a locally parameterized continuation technique that employs a predictor-corrector algorithm. The predictor algorithm helps to predict the solutions along a tangential direction passing through a point of known solution (base case to start with). The tangent predictor is determined by partially differentiating equation (3) on either side. Factorization of the resulting equation and a systematic arrangement gives the matrix form as shown in equation (4).

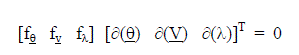A suitable solution of equation (4) gives the desired tangent vectors, [(θ)(V)(λ)]T. The next attempt is to select a suitable step size (Ã¯ÂÂ³) that predicts the length of the tangent vector [τ(θ) τ(V) τ(λ)]T as indicated in equation (5). Using the tangent predictor, [τ(θ) τ(V) τ(λ)]T, the new set of predicted solutions are obtained as mentioned in equation (6).

Once a predicted solution for a new loading level is obtained, the next step is to correct it through a corrector algorithm. The corrector algorithm is based on a locally parameterization technique that employs the conventional load flow program in a slightly modified form. The modification used is to specify any one parameter out of , V or as a continuation parameter. A proper selection of the continuation parameter helps to get the converged corrected solutions for the predicted ones. The process is repeated until the critical point is reached. The critical point is sensed by monitoring the magnitude and sign of the tangent vector corresponding to the load parameter, i.e. (λ). The value of (λ) is positive before the critical point, which turns zero at critical point and negative beyond it.

IMPLEMENTATION AND RESULTS

Examples of IEEE 14-bus test system shown in Fig.2 and IEEE 30-bus test system are studied in this paper. The line data and bus data for IEEE 14-bus and IEEE 30-bus test system are obtained from [10, 11]. It is observed that with parallel uniform load growth at all the system load buses, bus-9 in IEEE 14-bus system, and bus-21 in IEEE 30-bus system are the critical ones to suffer voltage instability without any contingency. In the next step different contingency cases are simulated as per the structure shown in Table I and Table II. The maximum number of lines considered for outage for particular test system is limited to 10-15% of existing lines in that system

The schemes described in Table I and Table II have been incorporated in the program to find out the critical loading level (λc) for each contingency case with the help of Newton-Raphson technique augmented by continuation power flow approach. The results indicating critical ranking of the contingency cases for both IEEE-14 bus and IEEE-30 bus test systems are presented in Table III. The following observations are made from the results.

(i) Convergence is obtained in the vicinity of the nose point for each contingency condition within the stipulated iterations as defined by the program.

(ii) Critical loading level (λc) is different for different contingency condition.

(iii) Critical loading level (λc) is higher for less severe contingency condition and is the least for most severe contingency condition.

(iv) The trend of critical loading level (λc) signifies that maximum power transfer capability of the network reduces with increasing order of severity of the contingency condition.

(v) Hence, selection and monitoring of critical loading level (λc) as a true indicator of the severity ranking of contingency conditions id well justified.

CONCLUSIONS

The steady state voltage stability analysis and congestion of power flow in deciding the maximum power transfer capability of the network subject to various contingency conditions have been dealt in this paper. In steady state analysis, power flow results have been obtained keeping in view composite loads at the system buses and a uniform load growth taken as snapshots in a time frame. These results are helpful for tracing the family of P-V and Q-V curves, which also indicate the critical power transfer capability of the network. Later, the line outage cases have been simulated for studying the effect of contingencies on load buses. A scheme for identification of the critical bus is presented based on calculation of post-contingency requirement of reactive power to avoid voltage collapse. It has been observed that the power transfer capability of the network gets significantly reduced following line outages and the load bus voltage suffers from an instant dip. The authors feel that these results will definitely enrich the past studies in the area of voltage stability. The above results have been obtained considering an off-line simulation technique. The authors also believe that the proposed method can also be applied for an on-line application.

Tables at a glance


Table 1	Table 2	Table 3

Figures at a glance


Figure 1	Figure 2

References

Y. T. Yoon, S. G. Raikar, M. D. Llic, “Project on Congestion Management for large scale power systems” Energy lab publication, Massachusetts Institute of Technology, Cambridge, MIT-EL-00-003WP, May.2000.
J. P. Leotard, M. D. Llic: “On the objectives of transmission pricing on the open access”. IEEE Power Engg Society, Winter Meeting, NewYork, vol.1, PP.476-483, 1999.
C. W. Taylor, “Power System Voltage Stability”, Mc Graw-Hill Publication, 1993.
A. Tiranuchit, R. J. Thomas, “A Posturing Strategy Against Voltage Instabilities in Electric Power Systems”, IEEE Transactions on Power Systems, Vol-3, pp.87-93, Feb.1988.
T. Van Cutsem, “A Method to Compute Reactive Power Margins with Respect to Voltage Collapse”, IEEE Transactions on Power Systems, Vol-6(1), pp.145-156, Feb.1991.
P. Kundur, K. Morison, B. Gao, “Practical Considerations in Voltage Stability Assessment”, International Journal of Electrical Power and Energy Systems, Vol.15(4), pp.205-215, Aug.1993.
V. Ajjarapu, S. Batula, “Effect of Load Modeling on Steady State Voltage Stability”, Electric Machines and Power Systems, Vol.23(5), pp.501-514, 1995.
IEEE Taskforce on Load Representation for Dynamic Performance, “Load Representation for Dynamic Performance Analysis”, IEEE Transactions on Power Systems, Vol-8(2), pp.416-423, 1992.
V. Ajjarapu, C. Christy, “The Continuation Power Flow: A Tool for Steady State Voltage Stability Analysis”, IEEE Transactions on Power Systems, Vol-7(1), pp.416-423, 1992.
Y. Wallach, “Calculation and Programs for Power System Network”, Prentice Hall Publication, Englewood Cliffs, 1986.
Tarek A. M. Sharaf, “System Loadability Versus Bus Loadability for Voltage Instability”, Electric Machines and Power Systems,Vol.24,pp.681-694, 1996.