International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

DEBRIS FLOW HAZARD ZONATION BY PROBABILISTIC ANALYSIS (MT. WOOMYEON, SEOUL, KOREA)

Dowon Park1, Seungrae Lee2, Nikhil N.V.3, Shinhang Kang4, Junyoung Park5
 M.S. Candidate, Department of Civil and Environmental Engineering, KAIST, 305-701, Daejeon,Korea 1,4,5
Professor, Department of Civil and Environmental Engineering, KAIST, 305-701, Daejeon,Korea2
Ph.D. Candidate, Department of Civil and Environmental Engineering, KAIST, 305-701, Daejeon,Korea3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper presents the application results of a regional,distributed empirical model: Flow path assessment of gravitational hazards at a Regional scale: (Flow-R) for a catchment on Woomyeon Mountain, Seoul, Korea. This model couples probabilistic and energetic algorithms for assessing of the spreading of flow and maximum runout distance. Flow-R also adopts the Geographic Information Systems (GIS) framework for determining the debris flow susceptibility for the whole mountain. In this paper,susceptibility scenarios have been simulated taking into account different source and propagation parameters.The best-fit values for the minimum plan curvature for initiating debris flow and the travel angle (vertical elevation to horizontal distance ratio) of runout distance were found to be -1/100 𝒎−𝟏 and 13°, and the resulting propagation on one of the calibration site was validated using the simplified frictionlimited model.Based on the results, the use ofthis model can be considered an important tool for debris flow analysis, especially in areas where related properties of the debris flow are not well defined.

Keywords
Flow-R,Woomyeon, GIS, Susceptibility map, Plan curvature, Travel angle, Net efficiency

INTRODUCTION
Physical modelling of debris flows in a wide area is difficult because of the complexity of the phenomenon and the variability of controlling factors. However, it is still necessary toidentify the hazard areasby debris flowsat regional scale and to describe the threat. This is because, nowaday a number of debris flow events have been occurred at the same time.The Woomyeon mountain debris flow in Seoul is an example for these severe events. In order to reduce risk posed by debris flows, research identifying the hazard areasby debris flows and describing the threat play animportant role. Thus, debris flow susceptibility modelling at regional scale hasbeen a subject of various studies in the last decades (Horton et al., 2008). As a result, there are a number of models adopting both empirical and deterministic approaches for predicting debris flow. However, the process based models of debris flow are difficult to apply because of the complexity of the phenomenon and the variability of controlling factors.These physical variables that control the mechanism of debris flows, also cannot be acquired over wide areas at reasonable cost (Lari et al, 2011). Empirical models offer an alternative,not only general low data availability but also large scale assessment (Kappes et al, 2011). In this study a coupled susceptibility analysismodel using probabilistic and energetic algorithms, Flow-R, was carriedout for Mt. Woomyeon area, situated in Seoul. Flow-R(Flow path assessment of gravitational hazards at a Regional scale), developed at the University of Lausanne in Swiss, aims at giving a regional assessment of debris flows susceptibility with minimum data requirement (Horton et al,2013). This program is based on the Matlab and available free of charge. Because of a paucity of input data which reflect Korean condition, we focuson parametric analyses to calibrate and test the model. The Flow-R model simulation resulted in reasonable estimates of debris flow initiation and spreading distance of reach. It can be found that the Flow-R model is applicable to catchments in mountainous terrain of Korea with limited data availability.

II. CASE STUDY
A. Study Area
The study area was Woomyeon Mountain, which is located in Seocho district of Seoul City, South Korea (Fig. 2). It is located at 37° 27′ 23″ - 37° 28′ 55″ N latitude and 126° 59′ 20″ - 127° 01′ 28″ E longitude. The elevation of WoomyeonMountain is 293 m above sea level. This area completely encircled by buildings and roads amounts to 5,104,162 m2 and is predominantly covered by forest, mostly oak trees. The Mt. Woomyeon range is basically composed of Pre-Cambrian banded biotite gneiss and granitic gneiss as depicted in Fig. 2. The banded biotite gneiss was moderately weathered and has stripes called gneissic banding, which develops under conditions of high temperature and pressure. Because of the gneissic banding, it is clear that the study area has been exposed to extreme shearing. Sixty percent of the study areais between 50 m and 150 m of elevation, while 67%of the slope angles are between 10 and 25 degrees. Hillslope is mostly toward S and E (about 14%, respectively) and display similar region of convex and concave (Fig. 1). The soil profile can be divided into three main layers (Korean Geotechnical Society, 2011): (1) colluvium layer extends to a maximum depth of 3.0 m from the ground level and the upper part of this layer was formed from previously transported soil. This layer is generally loose material composed of gravel and silty-sand, according to the Unified Soil Classification System (USCS), a heterogeneous, incoherent and permeable soil. (2) A transition zone is composed of mainly a clay layer (depth: 0.2 m to 0.5 m) characterized by the colors taupe and dark brown. It was anticipated that landslides would be generated by conditions in this layer between the colluvium and bedrock. (3) A subsoilof stiff weathered bedrock is followed by a clay layer. This subsoil layer can be considered impervious according to the low hydraulic conductivity indicated by the modelling that follows.
B. Debris Flow Event
In the area of Mt. Woomyeon, a number of catastrophic, debris flow events were triggered by a localized torrential rainfall from July 26 to July 27in 2011. During severe storms, the failed soil mass rapidly propagated downslope and increased its initial volume through erosion of in-place soils producing a dangerous mobilized volume. These mixtures of debris flowed down the roadways into local communities. Sixteen people were killed and ten buildings were damaged by the debris, leading to economic losses of about US$15 million.Fig.2(b and c) depicts the damaged districts (destroyed buildings, inundated areas, and debris flow channels)after the disaster. The average length of debris flows in the study areawas about 317.0 m, with an average volume of 269m3. The biggest debris flow has a length of 1365 m while the smallest is less than several tens of meters (Korean Society of Civil Engineers and Korean Geotechnical Society, 2012).

III. THEORETICAL BASIS OF FLOW-R
Application of the model can be divided into two main steps based on a digital elevation model: (1) source areas are first identified by means of geomorphological and userdefined criteria. (2)debris flows arepropagated from these sources on the basis of flow direction algorithms and frictional laws. Fig. 2 depicts above procedure using conceptual diagram. The debris flow volume andmass are not considered since accurate values cannotbe easily assessed over a large area.During the motion, significant mass changesoccur through erosion and deposition. Because the model is described in detail by Hortonet al. (2013), only a brief explanation is represented here.
A. Identification of Sources
For the identification of possible debris flow source areas;slope, and flow accumulation, as well as plan curvature were used for modelling in each DEM cell. These parameters are related withthree critical factors affecting directly or indirectly for the debris flow initiation: sediment availability, water input and slope gradient (Takahashi, 1981; Rickenmann and Zimmermann,1993).The sediment availability is related to the lithology in a geology map and the upslope contributing area is taken into account for water input because it is the same as precipitation region. The slope angle is a major criteriondue to its influence on the shear strength of a soil. Moreover, the plancurvature for detecting gully and landuse/cover map are added to increase the detection quality.
1) Slope angle
In the case of slope angle, most debris flows occur in areas with a gradient higher than 15° (Takahashi, 1981; Rickenmann and Zimmermann,1993). Thus, all cells with slope angle lower than 15° were excluded in this analysis.
2) Upslope area
The upslope contributing area was taken into accountas a characteristic of water input because it can represent the amount of water through the cell. The debris flow initiation threshold between slope angle and contributing area were expressed by anempirical relationship based on observations of Rickenmann andZimmermann (1993) and Heinimann (1998) as shown in Fig.3. The two equations representing rare events and extreme events respectively are the following (Horton et al., 2013):
wheretanβthres is theslope threshold, and Suca is the surface ofthe upslope contributing area. In this analysis, an “extreme fitting” curve was selected among two curves, as it covers ahigher possibility for debris flow initiation than rare fitting. All cells above this threshold were considered from possible sources area according to empirical observations.
3) Plan curvature
Debris flow sources are identified in the region where curvature is concave (Delmonacoet al,2003; Wieczoreket al,1997). The plan curvature which is perpendicular to the steepest slopeprovides recognition of gullies that are considered as debris flow potential sources. Fisher et al. (2012) considered values of -0.5/100 m−1 to -1.5/100 m−1 for accuracy in Norway. This value, also, was set to –2/100 ��−1according to the experience of Hortonet al. (2008) in the Canton de Vaud, Switzerland.However, there is no admitted threshold in the literature. This threshold is expected to be differentaccording to the location, type of debris flows as well asaccuracy of DEM (Hortonet al, 2013).
4) Other datasets
Any other dataset based on GIS can also be considered, such as geologicalmaps or land use mapsto remove inaccurate source areas.For example, outcropping or sub-outcropping rocks in geology map and built-up areas in landuse map should be excluded from possible debris flow source area. In the simulations carried out in this study, these maps did not consider because there is no debris flow in non-occurring condition. Finallyall classified input parameters wereintegratedin order to determine the possible location of debrisflow source. If pixel is determined as possible debrisflow source and never excluded are assigned assources at least once, this cell can become debris flow source.
B. Runout and Spreading Modelling
In a second step, the maximumrunout propagation is calculated both starting from the previously determined sources and usingtwo types of functions: flow direction and runout distancealgorithms.
1) Flow direction
Severalalgorithms for the representation of flow directions, using rectangular grid digital elevation models, are available: D8 (O’Callaghan and Mark, 1984), D infinity algorithm (Tarboton, 1997), multiple direction method (Quinn et al., 1991)and its modification (Holmgren, 1994). In the D8 and D infinity methods, water flows down one or two cells by partitioning the flow between the two cells nearest to the steepest downward slope direction. On the other hand, the multiple direction method and the modified multiple flowdirection methodspreading theflow on a percentage basis over several neighbouring downslope pixels are more realistic. The modified multiple flowdirection method was used because it is physically more realistic. The modified multiple flowdirection method after Holmgren (1994) is represented by thefollowing equation:
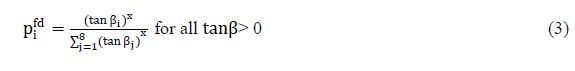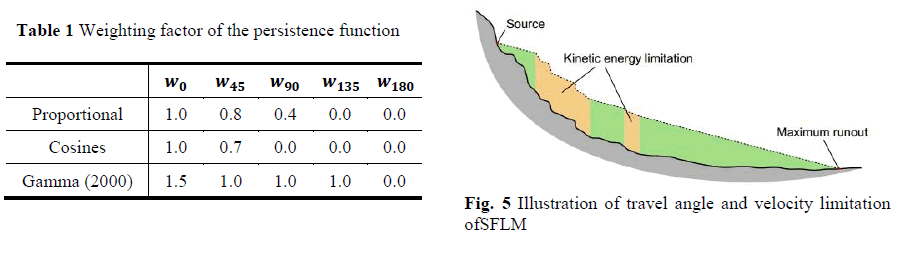
wherei, j are the flow directions, pi fd is the susceptibility proportion in direction i, tanβi is the slope gradient between the central cell and the cell in direction i, and x is the variable exponent. In case of x = 1, the spreading is similarto the multiple flow direction by Quinn et al. (1991), and the divergence is reduced asx increases. Also, it can be a single flow direction when x →∞. This factor can control degree of spreading and thus allows us to reproduce a wide range of other flow accumulations;e.g., debris flows, rock falls, avalanches, and floods (Kappeset al, 2012).For a debris flow case, Holmgren (1994)proposed a range of x between 4 and 6 in the Eq. (3).In this analysis, 4 was selected for the wide spread modelling as proposed by Claessenset al. (2005) and Horton et al. (2008). In addition to the influenceof slope, the effect of the flow inertia is considered for flow direction. Table 1 presents three implementations of the persistence. Based on the result of Gamma(2000), persistence weight for each cell was implemented in this study. For 0°, a persistence weight of 1 is assigned,for 45° 0.8, for 90° 0.4, for 135° and for 180° 0 as depicted in Table 1.Thus the final probabilities arethe combination of the spreading and the persistence.
where i, j are the flow directions, pi is the susceptibility value in direction i, pi fd is the flow proportion according to the flow direction algorithm, pi p is the flow proportion according to the persistence, and po is the previously determined susceptibility value of the central cell.
2) Propagation
The maximum distance reached by the debris flow is computed with basic energybased calculations without considering sourcemasses since they are mostly unknown in regional analyses. Thus, the soil mass that cannot bereached has a kinetic energy set to zero.This approach doesnot aim to represent the accurate physical processes, but to obtain a realistic result. The kinetic energy Ekin i at the time step iisobtained by the following formula:
whereEkin i is the kinetic energy of the cell in direction i, Ekin 0 is the kinetic energy of the central cell, ΔEpot i is the change in potential energy to the cell in direction i, and Ef i is the energy lost in friction to the cell in direction i. This energy based spreading algorithm controls spreading area of debris mass using energy balance, a friction loss function and maximum velocity threshold. First, the friction lossEf i can be assessed by two algorithms: the two parameters friction model by Perla etal. (1980) and the simplified frictionlimited model (hereafter, SFLM). Both methods can result in similar propagation areas, depending on the parameters (Jaboyedoffet al., 2011).Because the formal model was described in detail by Perlaet al. (1980), only a brief explanation is given here. This model was developed for avalanches, but has also been used for debris flows (Zimmermann et al., 1997). It is based on non-linear friction law using mass to drag ratio and friction coefficient. The difficulty is to knowthese values, because they change along the flow path. However, the SFLM method is more preferred since it has only 1 variable. This modelestimates the maximum possible runout distance using a minimum travel angle,also named a reach angle. Fig. 4 represents the basic concept of SFLM. The travel angle is computed by connecting a line between source area and the most distant point reached by the debris flow along itspath:
whereEf iis the energy lost in friction from the central cell to the cell in direction i, Δx is the increment of horizontal displacement, tanφthe gradient of the energy line, and g theacceleration due to gravity.Reviewing a number of cases in the world, the angle of travel has a range of 5°~15°. Lower angle implies the result of the worstcase analysis or wide spreading. Second, the kinetic energy is limited by a upper velocity threshold for estimating realistic kinetic energy. The 15m/s is reasonable for debris flow based on the observed maximum velocity of the overlapping flows in Swiss (Horton, 2008; Blahutet al, 2010).

IV. APPLICATION OF THE MODEL
In the simulations carried out in this study, different plan curvature and travel angle were considered for calibration. The plan curvature is perpendicular to the steepest slope and provides source of debris flow. By identifying gullies, it allows refining the delineation of the source areas. Second, travel angle is the angle of the line connecting the source areato the mass deposit reached by the debris flow. This concept enables the estimationof the deposit if the source area isknown.This angle corresponds to the propagation distance and it is calledFahr-böschung(Heim,1932). The most important dataset is the DEM. For Mt. Woomyeon, topographic analyses for elevation, slope angle, flow accumulation and curvature were calculated from 1:5000 maps developed by the National Geographic Information Institute. The ArcGIS was used to create grids with 10 m cells and to quantify the aforementioned information above for each cell of the DEM. Horton et al. (2013) conducted Flow-R analysis using 1 m,2 m, 5 m, 10 m, 25 m, and 50 m resolution DEM to verify sensitivity between grid sizes and analysis results. As a result, they pointed out that 10m DEM resolution satisfies reasonable propagation extent with Holmgren’s algorithm. Moreover, lower cell sizes do not bringsignificant information, even though they certainly lead to an increaseof computation time. These are consistent with the results of Zhang andMontgomery (1994) and Quinn et al. (1995)who concluded that 10 m grid size is recommended for landslide assessment as well as flow direction algorithm. Any other datasets based on GIS such as geologicalmaps or land use maps are notconsidered due to homogeneous soil and landuse condition.
A. Source Thresholds
As for the case of Mt. Woomyeon, the standard geomorphological data;e.g., slope, flow accumulation and curvature were integrated with the following parameters:
 Elevation: no criteria  Slope threshold: 15°  Flow accumulation – slope relationship: extreme threshold  Plan curvature: -1/100 ~ -2/100 m−1 (the range used in this study)
There is no threshold value for plan curvature in the literature. Plan curvature is inferredto differentvalues according to the several conditions as mentioned before. To know the plan curvatureinput value in Korea roughly, we searched plan curvature in this study with reference values listed in Table 2. On the basis of thescarce literature, a plan curvaturerange of -0.1/100 ~ -2/100 ��−1 was assumed.
B. Propagation Thresholds
Propagation parameters were taken from the literature in case of well supported by both physical and empirical backgrounds.
 Directions algorithm: Holmgren’s modified algorithm,with an exponentof 4  Inertial algorithm: Gamma(2000)  Velocity threshold : 28 m/s  The friction loss function: SFLM, with a travel angle of5°~15° (the range used in this study)
The maximum velocity threshold of debris flow mass used in this study was deduced from observed velocity of the event. Among many debris flows, Fig. 6(a) and (b) show the observed velocity of the event for Raemian and Sindonga apartment basin, respectively. Based on the CCTV and Black box in the damaged car at that time, themaximum velocity of the Mt. Woomyeon debris flow was estimated to be 28 m/s. This velocity is higher than other countries’ values since there was much water on slope just before the event. It means that the concentration of debris mass was very low. As for the plan curvature, various travel angles has been chosen according to the characteristics of debris flow for each region. Table 3 represents angle of the line connecting the source area to the most remote deposit reached by the debris flow in literature. Reviewing a number of cases in the world, the minimum angle of travel has a range of 5°~15°. For the Korean condition, a travel angle was assumed from the list summarized in Table 3.Afterwards, Flow-R analysis was performed using Woomyeon case study for verification.

V. RESULTS AND DISCUSSION
At regional scale within GIS environment, the analysis of spatial probability estimation was performed for the debris flow susceptibility.This kind of approach requires thecomparison of debris flow that happened in the past witha set of environmental factors, in order to predict areasof debris flow initiation that have similar conditions, usingheuristic or statistical methods (Van Westenet al., 2005).To calibrate the parameters of debris flow, the documents of debris flow mapping using satellite images and aerial photographs taken after event, as well as field survey report by the Korean Society of Civil Engineers wereanalyzed. Afterwards, the parameters calibration was performed fortwo different parameters: 1) Plan curvature for debris flow source area, 2) Travel angle for debris flow propagation distance in keeping other conditions same. The rest conditions in this study were same.
The plan curvature and travel anglefor values ranging from -0.5/100 ��−1 to -2/100 ��−1 for the identification of initiation and from 5° to 15° for spreading of debris flow were used in Flow-R. The results were following.The results of the debris flow source mapwith different plan curvature thresholdsare presented in Fig.7. In case of -1/100 ��−1 in Fig. 7(b), A good correlation between the modelling results and the field observations was found in this study. High probability of debris flow was classified using color code with red.However, Fig .7(a) with plan curvature threshold of -2/100 m−1 shows some failure prediction cases.The blue circles depicting debris flow non-occurrencein Fig. 7is because of the plan curvature threshold. This indicatesthat an assumed minimum plan curvaturethreshold of -1/100 ��−1would besufficient to identify the source areas threatened by debris flowsin the Mt. Woomyeon.
In terms of reach angle, Flow-R simulation was conducted. As a result, the particular differencewas observed in the predicted debris flow scarp distribution according to different travel angle as shown in Fig. 8 and Fig. 9.For the three other cases, clear trend was visible. The case (a) in both Fig. 8 and Fig. 9 with travel angle 15° showsshort runout distance than debris flow mapping. It does notcompletely contain the area affected by the mapped debris flow events.Thus, different from what actually happen, there is no socio-economic impact to local communities. In contrast, case (c) over-estimatesthe hazard area due to high value of horizontal distance. As a comparison with other travel angles, the reach of propagation with angle 13° reasonably estimates debris flow hazard area. That is, the calibrated reach angle of 13° showed agood adjustment of the past event. In Korea, the maximum probable travel angle of debris flows was suggested by Choi and Paik (2012). They observed the former events (238 debris flow cases)including Mt. Woomyeon in Korea, and suggested the angle of 13° (H/L is 4.5) to a representative angle. This is well coincided with the simulated result. Besides, Kim and Hwang (2011) proposed that a mean travel angle in Inje, Korea is 11.5° (H/L is 4.93).
Although the approach presented here has its limitations and cannot reflect the exact physical behavior, it can provide preliminary assessmentover wide areas. Fig. 8 and 9 show debris flow hazard region predicted by the model. A good coherence between the simulated propagationarea and actual damage area was observed in theregion where major debris flow events occurred.In the framework of susceptibility mapping, the resulting areas are often larger than the observed events on the field. This is the reason why the predicted area is larger than observed debris flow scarp.

VI. CONCLUSION
This paper presented a probabilistic approach to assess the susceptibility of debris flow in a mountainous region in Seoul, Korea.Especially, we concentrated on parametric studies to take into account different source and propagation related parameters. This presented approach of debrisflow hazard analysis, associating detection of thesource areas with a simple assessment of the debris flowspreading, provide encouraging results for consequent hazard and riskstudies. From the calibration phase, the following source and runout characteristics were selected: plan curvature -1/100 ��−1; the maximum runout (shadow) angle13°. These debris flow characteristic propertiesreasonably estimatedthe initiation zone and runoff distance for the Mt. Woomyeon debris flow hazard based on GIS framework at regional scale. In conclusion, Flow-R successfully simulates the observed debris flow propagation path for Mt. Woomyeon case. Slight incoherence in the predicted travel length of spread area is due to non-consideration of rheology characteristics of flow. However, the debris flow propagations simulated with Flow-R adequately follow the channels, even if some over-estimated area created incoherentpaths. That is, observations of previous events in the same region were satisfyingly reproduced during the validation procedures.Debris flow modelling using this kind of approach has following advantages: (1) it provides susceptibility map over a large area, (2) it allows very fast computation, and (3) it gives useful results with minimum dataset.Further research can be carried out to improve the Flow-R model by adopting appropriate region based parameters.

ACKNOWLEDGEMENT
This study was supported by the National Research Foundation of Korea under the Ministry of Education, Science, Technology (under grant No. 2012M3A2A1 050974).

References
  1. Bathurst, J. C., Burton, A., Ward, T. J., “Debris flow runout and landslide sediment delivery model tests”, J. Hydraul. Eng.123, 410-419, 1997.
  2. Blahut, J., Horton, P., Sterlacchini, S., and Jaboyedoff, M.,“Debris flow hazard modelling on medium scale: Valtellina diTirano, Italy”, Nat. Hazards Earth Syst. Sci., 10, 2379–2390,doi:10.5194/nhess-10-2379-2010, 2010.
  3. Choi, D. Y. and Paik, J. C.,“Characteristics of runout distance of debris flows in Korea”, The journal of Korean Society of Civil Engineers, vol32, 3B, 193-201, 2012.
  4. Claessens, L., Heuvelink, G. B. M., Schoorl, J. M., and Veldkamp,A.,“DEM resolution effects on shallow landslide hazard and soilredistribution modeling”, Earth Surf. Proc. Land., 30, 461–477,doi:10.1002/esp.1155, 2005.
  5. Delmonaco, G., Leoni, G., Margottini, C., Puglisi, C. and Spizzichino, D.,“Large scale debris-flow hazard assessment: a geotechnical approach and GIS modeling”, Natural Hazards and Earth System Sciences, Vol. 3, pp. 443-455, 2003.
  6. Ellen, S. D., Mark, R. K., Wieczorek, G. F., Wentworth, C. M., Ramsey, D. W. and May, T. E.,“Map showing principal debris-flow source areas in the San Francisco Bay region, California”. U.S. Geological Survey Open-File Report, 97-745 E. 8 pp, 1997.
  7. Fischer, L., Rubensdotter, L., Sletten, K., Stalsberg, K., Melchiorre,C., Horton, P., and Jaboyedoff, M.,“Debris flow modeling for susceptibility mapping at regional to national scale in Norway”, Proceedings of the 11th International and 2nd North American Symposium on Landslides, 3–8 June 2012, Banff, Alberta, Canada,2012.
  8. Gamma, P.,“dfwalk – EinMurgang-SimulationsprogrammzurGefahrenzonierung”, GeographischesInstitut der UniversitatBern, 2000 (in German).
  9. Haeberli, W.,“Frequency and characteristics of glacier floodsin the Swiss Alps”. Annals of Glaciology, 4, 85–90, 1983.
  10. Heim, A., “Bergsturz und Menschenleben”,BeiblattzurVierteljahresschrift derNaturforschendenGesellschaft in Zürich. 1932.
  11. Heinimann, H. R.,“MethodenzurAnalyse und Bewertung vonNaturgefahren, Bundesamt fur Umwelt”, Wald und Landschaft(BUWAL), 85, 247 pp., 1998 (in German).
  12. Holmgren, P.,“Multiple flow direction algorithms for runoff modelling in grid based elevation models: An empirical evaluation”,Hydrol. Process., 8, 327–334, doi:10.1002/hyp.3360080405,1994.
  13. Horton, P., Jaboyedoff, M., and Bardou, E.,“Debris flow susceptibility mapping at a regional scale”, Proceedings of the 4th Canadian Conference on Geohazards, edited by: Locat, J., Perret, D.,Turmel, D., Demers, D., and Leroueil, S., Qu´ ebec, Canada, 20–24 May 2008, 339– 406, 2008.
  14. Horton, P., Jaboyedoff, M.,Rudaz, B., andZimmermann, M.,“Flow-R, a model for susceptibility mapping of debris flows and othergravitational hazards at a regional scale”, Nat. Hazards Earth Syst. Sci., 13, 869–885, doi:10.5194/nhess-13-869-2013, 2013.
  15. Huggel, C., Kaab, A., Haeberli, W., Teysseire, P., and Paul, F.,“Re-mote sensing based assessment of hazards from glacier lake out-bursts: a case study in the Swiss Alps”, Can. Geotech. J., 39, 316–330, doi:10.1139/t01-099, 2002.
  16. Jaboyedoff, M., Rudaz, B., and Horton, P.,“Concepts and parameterization of Perla and FLM model using Flow-R for debris flow”,Proceedings of the 5th Canadian Conference on Geotechniqueand Natural Hazards, 15–17 May 2011, Kelowna, BC, Canada,2011.
  17. Kappes, M. S., Gruber, K., Frigerio, S., Bell, R., Keiler,M., and Glade, T.,“The MultiRISK platform: The technical concept and application of a regional-scale multi-hazardexposure analysis tool”, Geomorphology, 151–152, 139–155,doi:10.1016/j.geomorph.2012.01.024, 2012.
  18. Kappes, M. S., Malet, J.-P., Remaitre, A., Horton, P., Jaboyedoff,M., and Bell, R.,“Assessment of debris-flow susceptibility atmedium-scale in the Barcelonnette Basin, France”, Nat. HazardsEarth Syst. Sci., 11, 627–641, doi:10.5194/nhess-11-627-2011,2011.
  19. Kim, G. H. and Hwang, J. S.,“The estimation of debris flow behaviors in injaelandslide area”, The journal of Korean Society of Surveying Geodesy Photogrammetry and Cartography, vol 29, 5, 535-541, 2011.
  20. Korean Geotechnical Society,“Research contract report: addition and complement causes survey of Mt. Woomyeon landslide”, 2011.
  21. Korean Society of Civil Engineers,“Research contract report: causes survey and restoration work of Mt. Woomyeon landslide”, 2012.
  22. Lari, S., Crosta, G.B., Frattini, P., Horton, P., and Jaboyedoff, M.,“Regional-scale debris-flow risk assessment for an alpine valley”.5th Int. Conf. on Debris-Flow Hazards Mitigation, Padua, Italy,Italian Journal of Engineering Geology and Environment, 933–940, doi:10.4408/IJEGE.2011-03.B-101, 2011.
  23. O’Callaghan, J. F. and Mark, D. M.,“The extraction of drainage net-works from digital elevation data”, Comput. Vision Graph., 28,328–344, doi:10.1016/S0734-189X(84)80011-0, 1984.
  24. Perla, R., Cheng, T. T., and McClung, D. M.,“A two-parametermodel of snow-avalanche motion”, J. Glaciol., 26, 197–207, 1980.
  25. Prochaska, A. B., Santi, P. M., Higgins, J. D., Cannon, S. H.,“Debris-flow runout predictions based on the average channel slope (ACS)”, Engineering Geology 98, 29–40, 2008.
  26. Quinn, P., Beven, K., and Lamb, R.,“The index: How tocalculate it and how to use it within the topmodel framework”, Hydrol. Process., 9, 161–182, doi:10.1002/hyp.3360090204, 1995.
  27. Quinn, P., Beven, K., Chevallier, P., and Planchon, O.,“The prediction of hillslope flow paths for distributed hydrological modelling using digital terrain models”, Hydrol. Process., 5, 59–79,doi:10.1002/hyp.3360050106, 1991.
  28. Rickenmann, D. and Zimmermann, M.,“The 1987 debris flows inSwitzerland: documentation and analysis”, Geomorphology, 8,175–189, doi:10.1016/0169-555X(93)90036-2, 1993.
  29. Takahashi, T.,“Estimation of potential debris flows and their hazardous zones: Soft countermeasures for a disaster”, Journal of Natural Disaster Science, 3, 57–89, 1981.
  30. Tarboton, D. G.,“A new method for the determination of flow directions and upslope areas in grid digital elevation models”, WaterResour. Res., 33, 309–319, doi:10.1029/96WR03137, 1997.
  31. Van Westen, C. J., van Asch, T. W. J., and Soeters, R.,“Landslidehazard and risk zonation: why is it still so difficult?”, B. Eng.Geol. Environ., 65, 176–184, 2005.
  32. Wieczorek, G.F., Mandrone, G. and DeCola, L.,“The Influence of Hillslope Shape on Debris-Flow Initiation”, ASCE (Editor), First International Conference Water Resources Engineering Division, San Francisco, CA, pp. 21-31, 1997
  33. Zhang, W. and Montgomery, D.,“Digital elevation model grid size,landscape representation, and hydrologic simulations”, Water Re-sour. Res.,30, 1019–1028, doi:10.1029/93WR03553, 1994.
  34. Zimmermann, M., Mani, P., and Gamma, P.,“Murganggefahr undKlimaanderung – ein GIS-basierterAnsatz, NFP 31 Schluss-bericht”, Hochschulverlagan der ETH, Zurich, 1997 (in German).