International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

DENOISING USING SOFT THRESHOLDING

Jeena Joy1, Salice Peter2, Neetha John3
  1. Assistant Professor, Department of EEE, M.A College of Engineering, Kothamangalam, India1
  2. Professor, Department of EEE, M .A College of Engineering, Kothamangalam, India2
  3. Assistant Professor, Department of EEE, M.A College of Engineering, Kothamangalam, India3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a comparative study of different wavelet denoising techniques and the results obtained were examined. The denoising process rejects noise by thresholding in the wavelet domain. It is observed that „rigrsure„ method gives optimum performance. Discrete wavelet transform has the benefit of giving a joint timefrequency representation of the signal. Also it is suitable for both stationary and non stationary signals and is the most appropriate system in the field of signal detection. Discrete wavelet transform is implemented through multi resolution analysis and digital filter banks

Keywords
Wavelet transform, discrete wavelet transform, thresholding , signal denoising

INTRODUCTION
Wavelets are functions that satisfy certain mathematical requirements and are used in representing data or other functions. Algorithms process data at different scales or resolutions. If we look at a signal (or a function) through a large “window,” we would notice gross features. Similarly, if we gaze at a signal through a small “window,” we would notice small features. The result in wavelet analysis is to see both the forest and the trees together. This makes study of wavelets interesting and useful.The data sets of many scientific experiments are corrupted with noise, either because of the data acquisition process, or because of environmental effects. A first pre-processing step in analysing such datasets is denoising, that is, estimating the unknown signal of interest from the available noisy data. There are several different approaches to denoise signals and images. Despite similar visual effects, there are subtle differences between denoising, de-blurring, smoothing and restoration.
Generally smoothing removes high frequency and retains low frequency (with blurring). De-blurring increases the sharpness signal features by boosting the high frequencies, whereas denoising tries to remove whatever noise is present regardless of the spectral content of a noisy signal .Restoration is a kind of denoising that tries to retrieve the original signal with optimal balancing of de-blurring and smoothing Wavelet transforms enable us to represent signals with a high degree of sparsity. This is the principle behind a non-linear wavelet based signal estimation technique known as wavelet denoising. Wavelet denoising attempts to remove the noise present in the signal while preserving the signal characteristics, regardless of its frequency content. Wavelet denoising must not be confused with smoothing. As already mentioned smoothing only removes the high frequencies and retains the lower ones.

WAVELET BASED DENOISING
The principal work on denoising is done by Donoho , which is based on thresholding the DWT of the signal. The method relies on the fact that noise commonly manifests itself as fine-grained structure in the signal, and WT provides a scale-based decomposition. Thus, most of the noise tends to be represented by the wavelet coefficients at finer scales. Discarding these coefficients would result in a natural filtering out of noise on the basis of scale. Because the coefficients at such scale also tend to be the primary carriers of edge information, the method of Donoho thresholds the wavelet coefficients to zero if their values are below a threshold. These coefficients are mostly those corresponding to the noise. The edge related coefficients of the signal on the other hand, are usually above the threshold.
An alternative approach to hard thresholding is the soft thresholding, which leads to less severe distortion of the signal of interest. Several approaches have been suggested for setting the threshold for each band of the wavelet decomposition. A common approach is to compute the sample variance of the coefficients in a band and set the threshold to some multiple of the deviation.
Wavelet denoising has wide range of application in signal processing as well as other fields. The signals may be one-dimensional, two-dimensional and three-dimensional. They carry useful information. Denoising (noise reduction) is the first step in many applications. Other applications include data mining, medical signal/image analysis (ECG, CT, etc.), radio astronomy image analysis etc.
Motivation to the thresholding idea is based on the assumptions that the decorrelating property of a wavelet transform creates a sparse signal: most untouched coefficients are zero or close to zero. Also noise is spread out equally along all coefficients.The noise level is not too high so that we can distinguish the signal wavelet coefficients from the noisy ones.
As it turns out, this method is indeed effective and thresholding is a simple and efficient method for noise reduction. Further, inserting zeros creates more sparsity in the wavelet domain and one can see a link between wavelet denoising and compression.
Hard and soft thresholding with threshold are defined as follows:
The hard thresholding operator is expressed in equation(1) as,
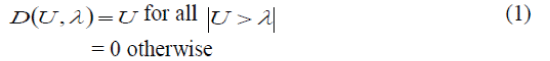image
The soft thresholding operator on the other hand is expressed in equation (2) as,
image
Hard threshold is a “keep or kill” procedure and is more intuitively appealing. The alternative, soft thresholding, shrinks coefficients above the threshold in absolute value. While at first sight hard thresholding may seem to be natural, the continuity of soft thresholding has some advantages. It makes algorithms mathematically more tractable. Sometimes, pure noise coefficients may pass the hard threshold and appear as annoying ‟blips‟ in the output. Soft thresholding shrinks these false structures.

THRESHOLDING ALGORITHMS
The choice of threshold is a fundamental issue. A very large threshold cuts too many coefficients, resulting in an over smoothing. Conversely, a too small threshold value allows many coefficients to be included in reconstruction, giving a wiggly, under smoothed estimate. The proper choice of threshold involves a careful balance of these principles. Most of the work is mainly due to Donoho and Johnstone. A variety of threshold choosing methods can be mainly divided into two categories: global thresholding and level−dependent thresholding. The former chooses a single value of to be applied globally to all empirical wavelet coefficients, while the later chooses different threshold value or each wavelet level j

A. Universal Thresholding - ‘sqtwolog’
This type of global thresholding method was proposed by Donoho and Johnstone. This is also called „sqtwolog‟ method. The threshold value is given in equation (3) as
image
where n is the number of data points, and ˆ is an estimate of the noise level σ. Donoho and Johnstone proposed an estimate of σ that is based only on the empirical wavelet coefficients at the highest resolution level J -1 because they consist most of noise. Most of the function information except the finest details is in lower level coefficients. The median of absolute deviation (MAD) estimator is expressed in equation (4) as
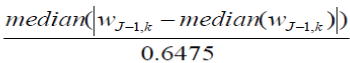image
The universal thresholding removes the noise efficiently. The fitted regression curve is often very smooth and hence visually appealing. If z1... zn represent the wavelet coefficients of the noise with idd N (0, σ2), then it is expressed in equation (5) as
image
This means that the probability of all noise being shrunk to zero is very high for large samples. Since the universal thresholding procedure is based on this asymptotic result, it sometimes does not perform well in small sample situations.

B. Minimax Thresholding
Mini max is another global thresholding method developed by Donoho and Johnstone.
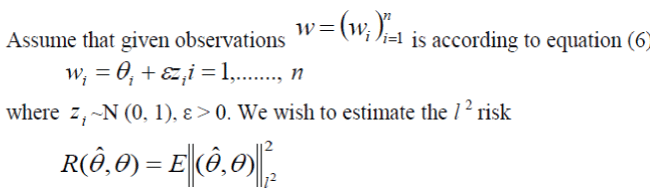image
Let be the soft thresholding function defined in equation (4.2). Suppose we have a single observation y~N (μ, 1). The function is defined in equation (8) as
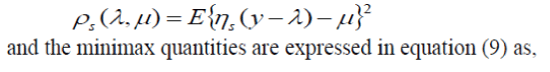image
image
image
Compared with universal threshold, the minimax thresholding is more conservative and is more proper when small details of function f lie in the noise range.

C. Sure Shrink – ‘rigrsure’
Sure Shrink chooses a threshold j λ by minimizing the Stein Unbiased Risk Estimate for each wavelet level j . It is also considered as „rigrsure‟ method.
image
where the function g =(gi) i-1 Rd to Rdis weakly differentiable.
Then the risk given by
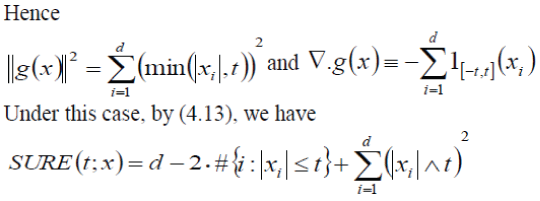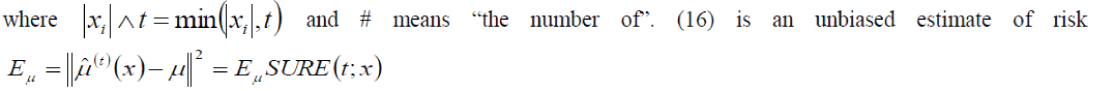image
image
image
image
By use of E SURE (t; x) as the estimator of risk, the SURE threshold is given by
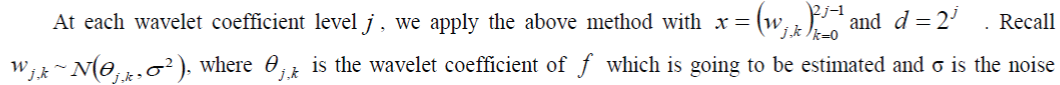image
image
level. In order to apply SureShrink method, we need to rescale j k w , by use of the MAD estimate in (4.4) for σ. The computational effort involved in minimizing the SURE criterion is light. Donoho show that the whole effort to calculate λ j in level j with d = 2 wavelet coefficients is O(d log(d) ).

D.‘heursure’ method
SureShrink does not perform well in certain cases that the wavelet representation at any level is very sparse, i.e., when the vast majority of coefficients are essentially zeros. Thus, Donoho suggest a mixture of universal threshold and SureShrink. If the set of coefficients is sparse, then the universal threshold is used; otherwise, SURE is applied. We call this hybrid method as Heursure.

IMPLIMENTATION – WAVELET DENOISING
The performance of four conventional denoising algorithms – namely „rigrsure‟, „heursure‟, „sqtwolog' and „ minimax „is compared .The denoising procedure is explained in the flow chart shown in Figure 1.
With the four methods, denoising is done. Type of thresholding used is soft thresholding. Denoised signal‟s performance is compared based on mean square error computed. This is implemented using Matlab tool box, which is widely used for high performance numerical computation and visualization The wavelet used is db4. Ingrid Daubechies invented what are called compactly supported orthonormal wavelets, thus making discrete wavelet analysis practicable. Daubechies wavelets are the most popular wavelets. They represent the foundations of wavelet signal processing and are used in numerous applications. The names of the Daubechies family wavelets are written dbN, where N is the order, and db the "surname" of the wavelets.
The performance measure chosen is the mean squared error (MSE) between denoised signal and the original signal as shown in Table 1.The variables in the set of experiments is different signal to noise ratio ranging from -15 to +15 including zero. If the mean square error is plotted against various SNR values, a graph as shown in figure2 is obtained.

CONCLUSION
Computational competence makes wavelet scheme attractive. The major observation from the set of experiments is that rigrsure gives best performance. It is observed that performance of minimax & heursure is better than that of sqtwolog. Denoising performance varies with type of signal under considerations and wavelet chosen.

ACKNOWLEDGMENT
We sincerely extend our thanks to each and every members of the staff in the Department of Electrical and Electronics Engineering, M A College of Engineering, Kothamangalam & PSG College of Technology, Coimbatore and every officials of NPOL, DRDO, Kochi, who guided us and rendered their full cooperation. Authors are immensely grateful to all those who have helped us directly or indirectly towards the successful completion of the paper.

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References
  1. Agostiino Abbate, Casinemer M.DeCusatis , Pankaj K Das, “ Wavelets and Sub bands”, Birkhauser, Boston, 2002
  2. Raghuveer M. Rao & Ajit S. Bopadiker , “Wavelet Transforms –Introduction to Theory and Applications", Pearson Education Asia, 1998.
  3. K.P. Soman & K. I. Ramachandran “Insight Into Wavelets -From Theory to Practice”, Prentice Hall, India, 2004
  4. Donoho, D.L. (1993), "Progress in wavelet analysis and WVD: a ten minute tour," in Progress in wavelet analysis and applications, Y. Meyer, S. Roques, pp. 109-128. Frontières Ed.
    5. <
  5. Donoho, D.L., I.M. Johnstone (1994), "Ideal spatial adaptation by wavelet shrinkage," Biometrika, vol 81, pp. 425-455.
  6. Donoho, D.L. (1995), "De-noising by soft-thresholding," IEEE Trans. on Inf. Theory, 41, 3, pp. 613-627
  7. G. Mallat. A wavelet tour of signal processing: the sparse way. 3rd edition, Academic Press, 2009
  8. www.mathwork.com
  9. www.wavelet.org.