Depth Estimation Analysis Using Sum of Absolute Difference Algorithm

Abstract

Stereo vision is one of the methods that can yield depth information of the scene. It uses stereo image pairs from two cameras to produce disparity maps that can be easily turn into depth maps. It is assumed that both the left and right channels of the multiview image sequence are coded using block or object-based methods. A dynamic programming algorithm is used to estimate a disparity field between each stereo image pair. Depth is then estimated and occlusions are optionally detected, based on the estimated disparity fields. Further, 2D and 3D motion compensation techniques are evaluated for the coding of sequences of depth or disparity maps. Reliability of depth maps and computational cost of algorithm is key issue for implementing real time robust applications. An algorithm for estimating reliable and accurate depth maps from stereoscopic image pairs is presented, which is based on correlation techniques for disparity estimation. By taking neighbouring disparity values into account, reliability and accuracy of the estimated disparity values are increased and the corona effect at disparity discontinuities is avoided. An interpolation of disparity values within segmented regions of homogeneous disparity enables the computation of dense depth maps by means of triangulation.

Keywords

STEREO MATCHING, DISPARITY, PSNR, MSE Error

INTRODUCTION

This Disparity means pixel displacement between corresponding points in multiview images or stereo images. Researchers have been giving special attention to stereo vision systems. Stereo vision systems aim at reconstructing 3D scenes by matching two or more images taken from slightly different viewpoints. Stereo vision systems generate accurate depth information of an observed scene. Most stereo vision implementations are based on two forward-facing cameras, where each camera delivers a 2D projection of a scene. The main difficulty encountered in this context is stereo matching which determines the spatial displacement between each two corresponding pixels in a stereo pair. This process is termed as correspondence problem and it aims at estimating a disparity map which is the set of disparity values of all the pixels in a reference image.

Intensive research has been conducted in the recent decades to solve the problem of finding the correspondences between the right and the left images. For more details, a good taxonomy of dense two-frame stereo matching algorithms can be found. In general, stereo matching algorithms can be categorized into two major classes: local and global methods. Global methods formulate the problem in terms of an energy function, which is subject to optimization. Then all disparities are determined simultaneously by applying energy minimization techniques. Global methods usually achieve high matching accuracy such as graph cuts dynamic programming and belief propagation. However, most of these methods are computationally expensive. Compared with them, local methods have higher efficiency and they are more suitable for real-time application. To retain more smoothness in the disparity map, local methods based on correlation are utilizing the colour or intensity values within a ?nite window. These methods have been widely employed, where a cost function is evaluated over a window around the pixel of interest. Correlation based methods fail in most points because they are strictly based on the resemblance constraint by assuming that the intensities of corresponding points are similar which is not robust to changes in illumination and contrast variation. Also, these methods are not able to deal with the problems of occluded areas and discontinuities where some parts of one image are hidden in the second image. Moreover, pixels inside texture less regions and repetitive patterns are hard to be properly matched.

STEREO MATCHING

The problem of reconstructing a three dimensional scene from several viewpoints was first investigated in the fields of aerial photography and human stereopsis. Until relatively recently, the scene reconstruction problem was typically treated as a matching problem where the objective was to match points or features between two or more images. Having obtained a match, the three dimensional position of a point could be determined by triangulation assuming the camera positions were known.

The matching of image points is performed by comparing a region in one image, referred to as the reference image, with potential matching regions in the other image and selecting the most likely match based on some similarity measure. The resulting scene estimate is then invariably represented using a depth-map relative to the reference camera. As an example of the stereo matching process, consider estimating the three dimensional position of a point P shown in Fig. 1. By correctly matching this point between the two images, the relative shift or displacement of the point can be used to calculate the depth of the point.

Stereo vision is obtained using two cameras which are displaced horizontally from each other in order to obtain different views of the same scene. Depth information can be obtained by examining the relative positions of objects in the two perspectives. Objects which are closer to the cameras will have a greater difference (disparity) in apparent position between the two perspectives. A disparity map can be formed from the combination of the 2 images that will allow a system to make decisions based on the distance of objects from the vehicle.

The main challenge in implementing stereo vision is developing an algorithm which is fast and returns good results. There are three main areas which make this a difficult challenge. The first and greatest challenge is that the creation of accurate disparity mappings of objects is a very computationally intense procedure as many comparisons have to be carried out between pixels in the two images returned by the stereo cameras. The second challenge is that many of the fast algorithms (e.g. Daniel Hutten ocher’s algorithm) are unable to distinguish homogenous regions. Homogeneous regions are areas of similar texture where the pixel values have little variation. Finally the third main challenge is that pixels which make up the same feature in each of the stereo images do not have the same values.

A. Solving the corresponding problem

The correspondence problem consists in finding correct point-to point correspond-dance between images or models. If we can identify the same 3D point in both views we can estimate its 3D coordinates. Accurately solving the correspondence problem is the key to accurately solving the Stereo Vision problem.

The fundamental hypothesis behind multi-image correspondence is that the appearance of any sufficiently small region in the world changes little from image to image. In general, appearance might emphasize higher-level descriptors over raw intensity values, but in its strongest sense, this hypothesis would mean that the color of any world point remains constant from image to image. In other words, if image point p and q are both images of some world point X, then the color values at p and q are equal. This color constancy (or brightness constancy in the case of grayscale images) hypothesis is in fact true with ideal cameras if all visible surfaces in the world are perfectly diffuse (i.e., Lambertian). In practice, given photometric camera calibration and typical scenes, color constancy holds well enough to justify its use by most algorithms for correspondence.

The geometry of the binocular imaging process also significantly prunes the set of Possible correspondences, from lying potentially anywhere within the 2D image, to lying necessarily somewhere along a 1D line embedded in that image [2] [3]. Suppose that we are looking for all corresponding image point pairs (p, q) involving a given point q (Figure 2). Then we know that the corresponding world point X, of which q is an image, must lie somewhere along the ray through q from the centre of projection Q. The image of this ray Qq in the other camera's image plane Π lies on a line l that is the intersection of Π with the plane spanned by the points P, Q and q. Because X lies on ray Qq, its projection p on Π must lie on the corresponding epipolar line l.(When corresponding epipolar lines lie on corresponding scan lines, the images are said to be rectified; the difference in coordinates of corresponding image points is called the disparity at those points.) This observation, that given one image point, a matching point in the other image must lie on the corresponding epipolar line, is called the epipolar constraint. Use of the epipolar constraint requires geometric camera calibration, and is what typically distinguishes stereo correspondence algorithms from other, more general correspondence algorithms.

Based on color constancy and the epipolar constraint, correspondence might proceed by matching every point in one image to every point with exactly the same Color in its corresponding epipolar line. However, this is obviously awed: there would be not only missed matches at the slightest deviation from color constancy, but also potentially many spurious matches from anything else that happens to be the same color. Moreover, with real cameras, sensor noise and finite pixel sizes lead to additional imprecision in solving the correspondence problem. It is apparent that color constancy and the epipolar constraint are not enough to determine correspondence with sufficient accuracy for reliable triangulation. Thus, some additional constraint is needed in order to reconstruct a meaningful three-dimensional model. Marr and Poggio proposed two such additional rules to guide binocular correspondence [3] [4].

STEREO MATCHING ALGORITHMS

Stereo Matching Algorithms like SAD (sum of absolute difference), use for finding the disparity use the stereo images.

A. SAD (Sum of Absolute Difference)

This algorithm is based on pixel based approach is use for finding the disparity. Sum of absolute differences (SAD) is an algorithm for measuring the similarity between image blocks. It works by taking the absolute difference between each pixel in the original block and the corresponding pixel in the block being used for comparison. These differences are summed to create a simple metric of block if the left and right images exactly match, the resultant will be zero.

The sum of absolute differences may be used for a variety of purposes, such as object recognition, the generation of disparity maps for stereo images, and motion estimation for video compression.

EVALUATION METHODOLOGY

Quality measures are computed with known ground truth data:

MSE

The Mean Square Error (MSE) and the Peak Signal to Noise Ratio (PSNR) are the two error metrics used to compare image compression quality.

The MSE represents the cumulative squared error between the compressed and the original image, whereas PSNR represents a measure of the peak error.

The lower the value of MSE, the lower the error.

OBSERVATIONS AND RESULTS

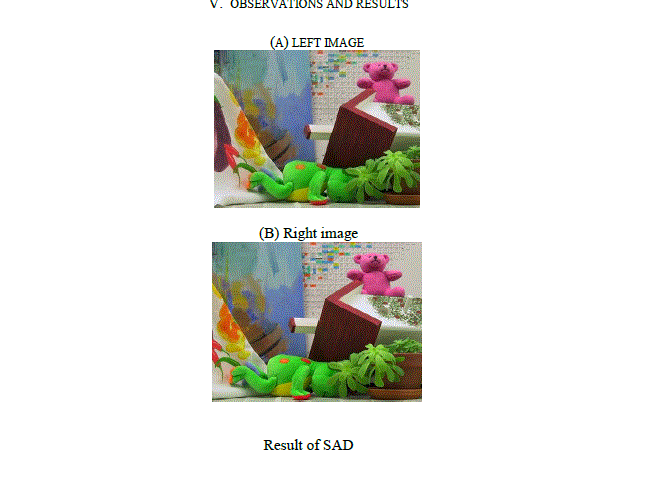CONCLUSION

Matlab R2007b has been chosen for implementing different Stereo Matching Algorithms. Stereo Matching Algorithms like SAD (sum of absolute difference), has been implemented to generate disparity Map. SAD gives good disparity Map. MSE error is small and gives more accurate PSNR.

FUTURE SCOPE

Disparity Maps are successfully generated by implementing through different type of Stereo Matching Algorithms, but still there is a scope for improvement. Performance of the Stereo Matching Algorithms is affected by the illumination conditions, shape and the camera characteristics. Effects of these three on disparity Map. Depth Map can be Generate. Height and Width of an object can also be tried to be calculated. 3D view can also be generated by using Disparity Map and Depth Map.

Figures at a glance

Figure 1 Figure 2 Figure 3

References

R. Gonzales, P.Wintz, woods, Digital Image Processing, Addition-Wesley, 1987 Nadir Nourain, Dawoud,Brahim, Belhaouri samir, josefina janier fast template matching method based optimized sum of absolute difference algorithm for face localization international journal of computer application vol.18 no8 ,march2011 A. Ian H. Witten, Eibe Frank, The Geometry from Multiple Images, MIT Press, 2000 D. Marr and T.Poggio, Computational Theory of Human Stereo Vision. D. Marr and T. Poggio, Cooperative Computation of Stereo Disparity. Daniel Scharstein and Richard Szeliski, A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. C. Lawrence and Kanade, A Cooperative Algorithm for Stereo Matching and Occlusion Detection. www.middlebury.edu