ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Prashant Upadhyay1, Bheru Das Vairagi1, Dr. Vinod Kumar2, Dr. R.R. Joshi3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Maximum power point trackers are so important to improve the efficiency of photovoltaic systems. Many methods have been proposed to achieve the maximum power that the PV modules are capable of producing under different atmospheric conditions. This paper proposed a fuzzy logic based Maximum Power Point Tracking (MPPT) algorithm for solar system. The solar panel is simulated and analyzed in MATLAB/SIMULINK. Photovoltaic system is connected to a DC-DC Buck-boost converter. The Solar panel can produce maximum power at a certain operating point called Maximum Power Point (MPP).To achieve maximum power and to get maximum efficiency, the whole system must operate at that Maximum Power point. Maximum power point of PV panel keeps same on changing with changing solar irradiance and temperature of cell. Then to obtain maximum power from a PV system, MPPT algorithms are implemented. So that, fuzzy logic based MPPT is developed and Simulation results show the effective of the fuzzy based controller to produce more stable power.
Keywords |
| MPPT, Fuzzy Logic, PV Modeling, Buck-Boost Converter. |
I. INTRODUCTION |
| As we know energy has the great role in our life and economy. The energy demand has greatly increased day by day due to the technical revolution. Fossil fuels have been started to be gradually depleted. On the other hand the greenhouse gases emissions are increasing due to the conventional generation of energy. It is a really critical challenge to reduce carbon dioxide emissions and ensuring safe, improve and affordable energy, and to achieve better energy systems. Renewable energy sources are considered for generation of clean and sustainable energy.[1] |
| There are many available renewable energy sources are such as solar energy, wind energy, etc. Photovoltaic (PV) system has a huge research area for upcoming energy requirement. So it taken a great attention by the researchers and it appears to be one of the most sustainable renewable energy sources. Solar energy is a secure, less maintenance, pollution free and noiseless generation due to absence of moving parts.[2,3] |
| However, two important factors affect the implementation of photovoltaic systems. These are high initial cost and less efficient at energy conversion. So to reduce photovoltaic system cost and to increases the conversion efficiency of solar energy, the maximum power point tracking system of photovoltaic modules is one of the effective method. Maximum power point tracking, frequently referred to as MPPT, is a system used to extract the maximum power of the PV module to deliver it to the load, and system efficiency increases. |
| PV systems are dependent power sources with nonlinear I-V characteristics under different environmental (insolation and temperature) conditions. In addition they have high installation cost and low energy conversion efficiency. These are the reasons for the less efficiency of PV systems. To overcome the problems, the Maximum power point tracking of the PV system is used (at a given condition) at on-line or off-line algorithms and the system operating point is forced toward this to desired condition.[4,5] |
| In literature, various maximum power point tracking (MPPT) techniques are proposed and implemented. These techniques include look-up table methods, perturbation and observation (P&O) methods and computational methods. One of the computational methods which have demonstrated fine performance using fuzzy-based MPPT technique.[6] |
| The fuzzy theory based on fuzzy logic sets and fuzzy algorithms provides a general method of expressing linguistic rules so that they may be processed quickly by a computer. Recently some application of fuzzy control has been successful in photovoltaic applications. The fuzzy controller introduced in uses dP/dI and its variations D(dP/dI) as the inputs and computes MPPT converter duty cycle.[7] The shortcoming of this approach is the ignorance of duty cycle variations, which results in an acceptable accuracy level with improved dynamic characteristics. The fuzzy tracker of reference considers variation of duty cycle, but replaces dP/dI by the variation of panel power. This tracker has fine dynamic behavior with limited accuracy.[8] |
| This paper presents a photovoltaic system including a solar panel, a fuzzy MPP tracker and a resistive load is designed, simulated and constructed. Simulated and measured results are presented. |
II. RELATED WORK |
| A. THE PHOTOVOLTAIC SYSTEM |
| There are many equivalent circuits of a solar cell, where the single-diode and two-diode models could be the mostly used. So that the single-diode model is simple and accurate enough in many cases. Its equivalent circuit with series and parallel resistance is shown in Figure 1.[3,4] |
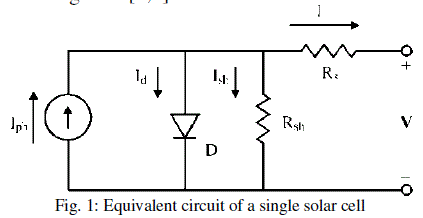 |
| The symbols in Fig. 1 are defined as follows: |
| Iph : photocurrent; |
| Id : current of parallel diode; |
| Ish : shunt current; |
| I : output current; |
| V : output voltage; |
| D : parallel diode; |
| Rsh : shunt resistance; |
| Rs : series resistance; |
| Using the equivalent circuit of Fig.1, the nonlinear I-V characteristics of solar cells is given by the following equation: |
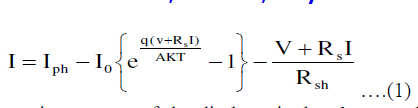 |
| Where Io is the reverse saturation current of the diode, q is the electron charge (1.602 × 10−19 C), A is the curve fitting factor, and K is Boltzmann constant (1.38 × 10−23J/K). |
| Model of a PV Module |
| If a solar cell type tends to have an I–V curve in which the slope at short circuit is almost zero, the value of Rsh can be assumed to be infinite. In this case, the last term in (1) could be ignored. And taking Iph as ISC, (1) will become |
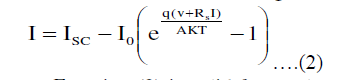 |
| Where ISC is the short-circuit current. Equation (2) is valid for a solar cell. For the accurate application of this equation for a PV module, the term of q(V + Rs I)/AKT is changed to q(V + Rs I)/NsAKT, in which Ns is the number of series-connected solar cells in a PV module. |
| A simple PV module model will be derived from (2) in this section. When a PV module is in a open-circuit situation, I = 0 and the item q/NsAKT in (2) will be solved as follows: |
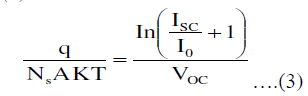 |
| where VOC is the open-circuit voltage of a PV module. Substituting (3) into (2), we get |
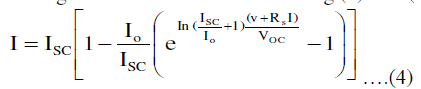 |
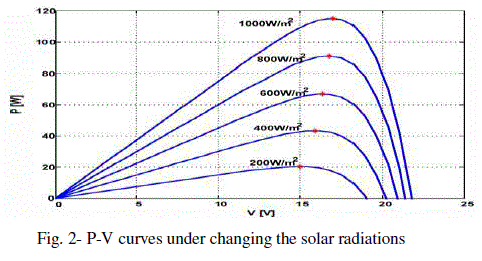
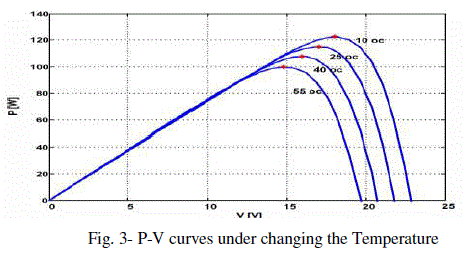
| Fig. 2 shows the P-V curves of the PV module under changing solar radiation from 200W/m2 to 1000W/m2 while keeping the temperature constant at 25°C. Fig. 3 shows the P-V curves of the PV module under changing temperature from 10°C to 55°C while keeping the solar radiation constant at 1000W/m2. |
 |
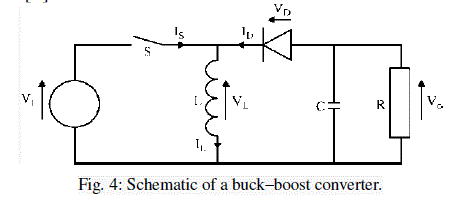
| B. DC-DC BUCK-BOOST CONVERTER |
| The DC-DC converter is an electronics circuit which is used to provide a loss less transfer of energy between different circuits at different DC voltage levels. There are many DC-DC converters. One of the popular types of DCDC converters is buck-boost converter. Buck-boost converter is circuit that operating using switching mode power supply. Buck-boost converter used to step up and step down the DC voltage by changing the duty ratio of the switch |
| When the duty ration is less than 0.5, the output voltage is less than the input voltage and vice versa. The buck-boost converter circuit is shown in Fig. 4.[9] |
 |
| The operation of the Buck-boost converter is as follows: |
| When the transistor is turned ON, the diode is reverse-biased and being not conducting. Turning on the transistor is accomplished during o < t < DT s interval. The voltage across the inductor in this stage is given as: |
| When the transistor is turned off, the diode is conducting. Turning on the transistor is accomplished during DTs< t < Ts interval. The voltage across the inductor in this stage is given as: |
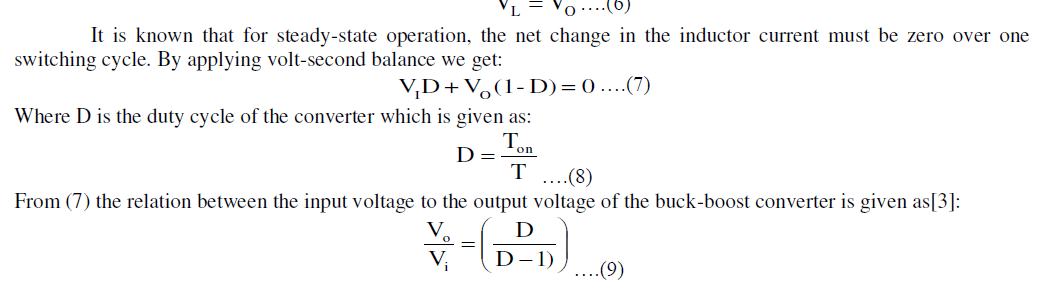 |
III. THE PROPOSED FUZZY LOGIC BASED MPPT METHOD |
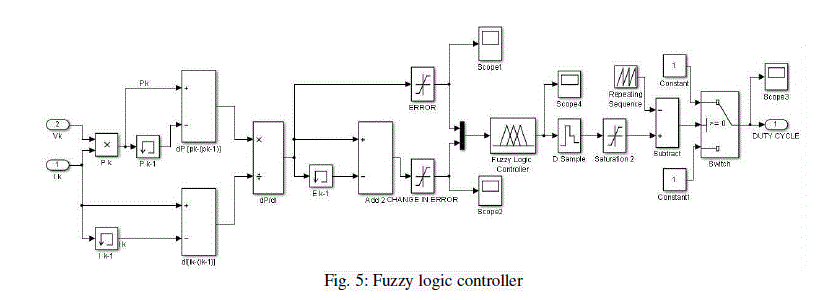
| A Fuzzy Logic Controller (FLC) is designed to work as an MPPT controller. Fig. 5 shows the FLC. |
 |
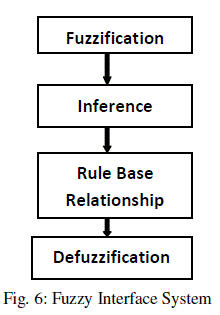
| The FLC contains a Fuzzy Inference System (FIS) whose structure is shown in Fig. 6. The FIS inputs, error (E) and |
| change in error (CE), are obtained using the following equations:[10] |
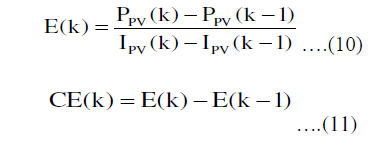 |
| Where: |
| PPV: The power of the PV system |
| IPV: The current of the PV system |
| E: Error |
| CE: Change in error |
 |
| A. Fuzzification: |
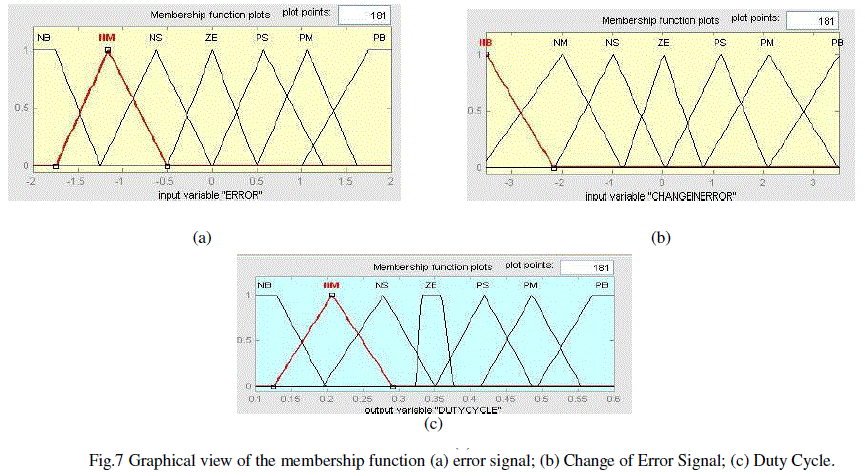
| 1) Fuzzification of Error-Signal: The range of error-signal is partitioned into seven regions with triangular and trapezoidal membership functions labeled as: Negative Big, Negative medium, Negative small, Zero error, positive small, positive Medium and positive big over Universe of Discourse (UoD) of -2 to 2 as shown in fig.7. |
| 2) Fuzzification of Change in Error-Signal: The second input parameter is Change in Error-Signal. The range of signal is partitioned into seven regions with triangular membership functions labeled as: Negative Big, Negative medium, Negative small, Zero error, positive small, positive Medium and positive big over UoD of -3.5 to 3.5 same as shown as error signal. |
| 3) Fuzzification of PWM Duty cycle-Signal: Defuzzification converts membership functions into Crisp value for PWM signal. Seven regions with triangular and trapezoidal membership partitions are labeled as: Negative Big, Negative medium, Negative small, Zero error, positive small, positive Medium and positive big over UoD of 0.1 to 0.6 counts. |
 |
 |
| B. Fuzzy Inference System: |
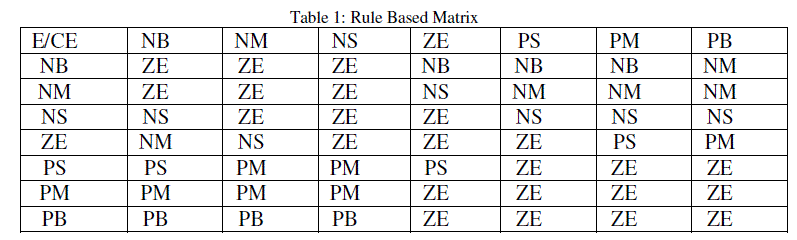
| The Fuzzy Inference forms a key part of Fuzzy Logic Control. The Fuzzy IF-THEN rule base matrix is in[11] |
 |
| C. Defuzzification: |
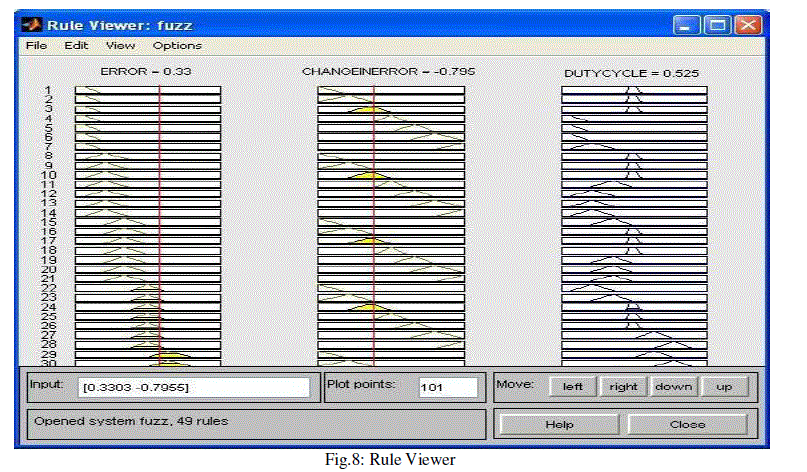
| The Fuzzy Inference based on Mamdani’s scheme is shown in fig.8 for present Error of 0.33, change of error is -0.795 thereby suggesting a PWM duty cycle of 0.525.[10,11] |
 |
IV. RESULT AND DISCUSSION |
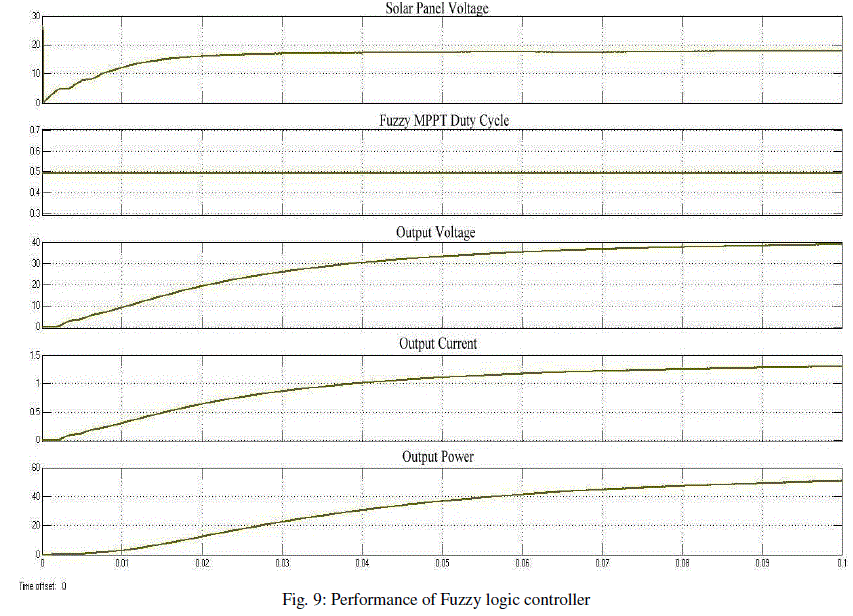
| In order to verify the MPP tracker for the photovoltaic simulation system, the proposed fuzzy MPPT method can effectively and accurately tracks the maximum power. The simulation is done using MATLAB/STMULINK. The output of the fuzzy MPPT control block is the gating signal which is used to drive the MOSFET. With further tuning of fuzzy sets and fuzzy rules the process of output power can be more and more power efficient. Results are shown in fig. 9. |
 |
V. CONCLUSION |
| Fuzzy MPPT model using Matlab/SIMULINK and design of appropriate DC-DC buck-boost converter with a maximum power point tracking facility are presented in this paper. A new method for MPPT based fuzzy logic controller is presented. The model is tested under 1000W/m2 solar radiation and 25’C photovoltaic temperature. Simulation results show that the proposed method effectively tracks the maximum power point as compared to other MPPT techniques. The oscillation around MPP is decreased and the response is faster in compared with the conventional methods. |
References |
|