DESIGN AND IMPLEMENTATION OF 31-
ORDER FIR LOW-PASS FILTER USING
MODIFIED DISTRIBUTED ARITHMETIC
BASED ON FPGA

Shrikant Patel

DESIGN AND IMPLEMENTATION OF 31- ORDER FIR LOW-PASS FILTER USING MODIFIED DISTRIBUTED ARITHMETIC BASED ON FPGA

Shrikant Patel
PG student, Department of Electronic and Communication, Oriental University, Indore, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper provide the principles of Modified Distributed Arithmetic, and introduce it into the FIR filters design, and then presents a 31-order FIR low-pass filter using Modified Distributed Arithmetic, which save considerable MAC blocks to decrease the circuit scale, meanwhile, divided LUT method is used to decrease the required memory units and pipeline structure is also used to increase the system speed. The implementation of FIR filters on FPGA based on traditional method costs considerable hardware resources, which goes against the decrease of circuit scale and the increase of system speed. It is very well known that the FIR filter consists of Delay elements, Multipliers and Adders. Because of usage of Multipliers in our design gives rise to 2 demerits that are (i) Increase in Area and (ii) Increase in the Delay which ultimately results in low performance (Less speed). A new design and implementation of FIR filters using Modified Distributed Arithmetic is provided in this paper to solve this problem. Modified Distributed Arithmetic structure is used to increase the recourse usage while pipeline structure is also used to increase the system speed. In addition, the divided LUT method is also used to decrease the required memory units. Modified Distributed Arithmetic can save considerable hardware resources through using LUT to take the place of MAC units. The simulation results indicate that FIR filters using Modified Distributed Arithmetic can work stable with high speed and can save almost less than 50 percent hardware recourses to decrease the circuit scale, and can be applied to a variety of areas for its great flexibility and high reliability. The main abstract of this paper design a FIR filter according to Modified Distributed Arithmetic, we can make a Look-Up-Table (LUT) to conserve the MAC values and callout the values according to the input data. Therefore, LUT can be created to take the place of MAC units so as to save the hardware resources.

Keywords

Distributed Arithmetic (DA), Field programmable gate arrays (FPGA), Finite impulse response (FIR), look up table (LUT), Pipeline.

INTRODUCTION

Filters are a basic component of all signal processing and telecommunication systems. Filters are widely employed in signal processing and communication systems in applications such as channel equalization, noise reduction, radar, audio processing, video processing, biomedical signal processing, and analysis of economic and financial data. For example in a radio receiver band-pass filters, or tuners, are used to extract the signals from a radio channel. Digital filters are divided into two categories, including Finite Impulse Response (FIR) and Infinite Impulse Response (IIR). And FIR filters are widely applied to a variety of digital signal processing areas for the virtues of providing linear phase and system stability.

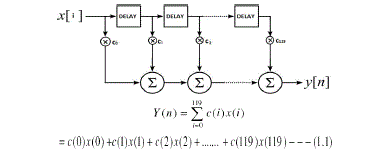c(i) =constant or filter coefficient

x(i) = nth point of input sequences is variable

y(n)= represents the system response

Finite impulse response (FIR) filters are the most popular type of filters implemented in software. A digital filter takes a digital input, gives a digital output, and consists of digital components. In a typical digital filtering application, software running on a digital signal processor (DSP) reads input samples from an A/D converter The FPGA-based FIR filters using traditional direct arithmetic costs considerable multiply-and-accumulate (MAC) blocks with the augment of the filter order. However, according to Distributed Arithmetic, we can make a Look-Up-Table (LUT) to conserve the MAC values and callout the values according to the input data if necessary. Therefore, LUT can be created to take the place of MAC units so as to save the hardware resources. This paper provide the principles of Distributed Arithmetic, and introduce it into the FIR filters design, and then presents a 31-order FIR low-pass filter using modified Distributed Arithmetic, which save considerable MAC blocks to decrease the circuit scale, meanwhile, divided LUT method is used to decrease the required memory units and pipeline structure is also used to increase the system speed.

DISTRIBUTED ARITHMETIC

The arithmetic sum of products that defines the response of linear, time-invariant networks can be expressed as:

Where:

y (n) = response of network at time n.

Xk (n) = ‘k’th input variable at time n.

AK = weighting factor of ‘k’th input variable that is constant for all n, and so it remains time-invariant In filtering applications the constants, Ak , are the filter coefficients and the variables, xk , are the prior samples of a single data source (for example, an analog to digital converter). In frequency transforming - whether the discrete Fourier or the fast Fourier transforms - the constants are the sine/cosine basis functions and the variables are a block of samples from a single data source. Examples of multiple data sources may be found in image processing. The multiply-intensive nature of can be appreciated by observing that a single output response requires the accumulation of K product terms. In DA the task of summing product terms is replaced by table look-up procedures that are easily implemented in the Xilinx configurable logic block (CLB) look-up table architecture. We start by defining the number format of the variable to be 2’s complement, fractional - a \standard practice for fixed-point microprocessors in order to bound number growth under multiplication. The constant factors, Ak, need not be so restricted, nor are they required to match the data word length, as is the case for the microprocessor. The constants may have a mixed integer and fractional format; they need not be defined at this time. The variable, xk, may be written in the fractional format as shown in

Where xkb is a binary variable and can assume only values of 0 and 1. A sign bit of value -1 is indicated by xk0. Note that the time index, n, has been dropped since it is not needed to continue the derivation. The final result is obtained by first substituting

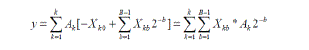and then explicitly expressing all the product terms under the summation symbols:

y= - [X10.A1+X20.A2+X30.A3+………...+Xk0.Ak]

+ [X11.A1+X21.A2+X31.A3+………...+Xk1.Ak]2-1

+ [X12.A1+X22.A2+X32.A3+………...+Xk2.Ak]2-2

+ [X1B-2.A1+X2B-2.A2+X3B-2.A3+………...+XkB-2.Ak]2-(B-2)

+ [X1B-1.A1+X2B-1.A2+X3B-1.A3+………...+XkB-1.Ak]2-(B-1)

FILTERS DESIGN

In the course of FIR filters design, ringing can be generated at the edge of transition band for the reason that finite series Fourier transform cannot produce sharp edges. So windows are often used to produce suitable transition band, and Kaiser Window is widely used for providing good performance. The parameter ÃÂ¡ÃÂµÃÂ is an important coefficient of Kaiser Window which involves the windows types. We can get a variety of windows like Rectangular window, Hanning window, Hamming window, and Blackman window with the adjustment of ÃÂ¡ÃÂµÃÂ. A 31-order FIR low-pass filter is designed using Kaiser Window, and the parameter is as follows: ÃÂ¡ÃÂµÃÂ=3.39, w=0.18. We can obtain the filter coefficients using Matlab as follows:

h(0)=h(31)=0.0019;h(1)=h(30)=0.0043;h(2)=h(29)=0.0062;h(3)=h(28)=0.0061;h(4)=h(27)=0.0025;h(5)=h(26)=- 0.0050;h(6)=h(25)=0.0148;h(7)=h(24)=0.0236;h(8)=h(23)=0.0266;h(9)=h(22)=0.0192;h(10)=h(21)=0.0015;h(11)=h(2 0)=0.0351;h(12)=h(19)=0.0774;h(13)=h(18)=0.1208;h(14)=h(17)=0.1566;h(15)=h(16)=0.1768.

In Matlab data is described in the floating-point form while described in the fixed-point form in this FPGA system. After quantizing the filter coefficients using 12-bit-width signed binary, we can obtain the final coefficients as follows:

h(0)=h(31)=4;h(1)=h(30)=9;h(2)=h(29)=13;h(3)=h(28)=12;h(4)=h(27)=5;h(5)=h(26)=-10;h(6)=h(25)=30;h(7)=h(24)=- 48;h(8)=h(23)=55;h(9)=h(22)=39;h(10)=h(21)=3;h(11)=h(20)=72;h(12)=h(19)=158;h(13)=h(18)=247;h(14)=h(17)=32 1;h(15)=h(16)= 362.

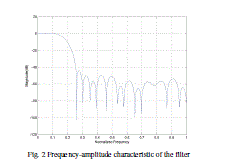
With above coefficients in Matlab, the frequency-amplitude characteristic of the filter is described as Fig.2.

As we are supposed to design 31-order filter, with the increase of filter order, the scale of LUT will increase dramatically, which will cost more time to look up the table and more memory to store the values. Therefore, we can divide the LUT unit into four small LUT units to solve this problem. Coefficient values of small LUT is given below

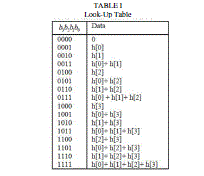DISTRIBUTED ARITHMETIC FOR FIR FILTER

Distributed Arithmetic is one of the most well-known methods of implementing FIR filters. The DA solves the computation of the inner product equation when the coefficients are pre knowledge, as happens in FIR filters. An FIR filter of length K is described as:

Where h[k] is the filter coefficient and x[k] is the input data. For the convenience of analysis, x'[k] =x [n - k] is used for modifying the equation (1) and we have:

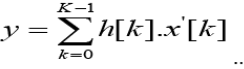Then we use B-bit two's complement binary numbers to represent the input data:

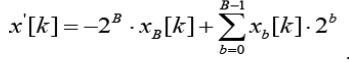Where Xb[k] denoted the b’th of Xb[k], Xb[k] €{0,1}. Substitution of (3) into (2) yields:

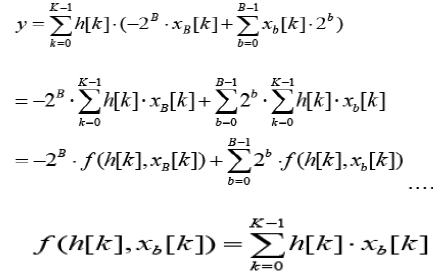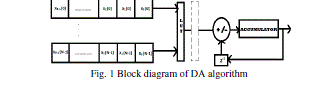
In equation (4), we observe that the filter coefficients can be pre-stored in LUT, and addressed by xb = [,,...]. This way, The implementation of digital filters using this arithmetic is done by using registers, memory resources and a scaling accumulator. Original LUT-based DA implementation of a 4-tap (K=4) FIR filter is shown in Figure 3. The DA architecture includes three units: the shift register unit, the DA-LUT unit, and the adder/shifter unit.

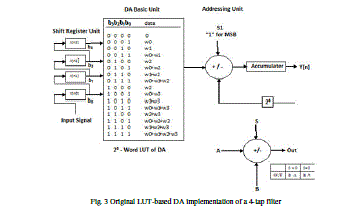As the filter order increases, the memory size also increases. This in turn increases the look up table (LUT) size. So we use combinational logic in place of look up table for better performance. The proposed DA-LUT unit dramatically reduces the memory usage, since all the LUT units can be replaced by multiplexers and full adders.

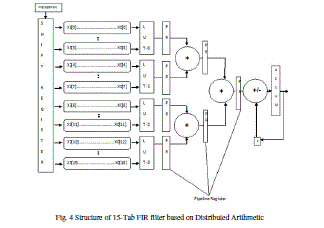Fig. 4 Structure of 15-Tab FIR filter based on Distributed Arithmetic

B. Modified Distributed Arithmetic LUT Architecture

In Fig.3, we can see that the lower half of LUT (locations where b3=1) is the same with the sum of the upper half of LUT (locations where b3 =0) and h [3]. Hence, LUT size can be reduced 1/2 with an additional 2x1 multiplexer and a full adder, as shown in Figure 5. By the same LUT reduction procedure, we can have the final LUT-less DA architectures, as shown in Figure 6 On other side, for the use of combination logic circuit, the filter performance will be affected. But when the taps of the filter is a prime, we can use 4-input LUT units with additional multiplexers and full adders to get the tradeoff between filter performance and small resource usage.

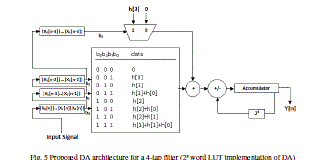Fig. 5 Proposed DA architecture for a 4-tap filter (2³ word LUT implementation of DA)

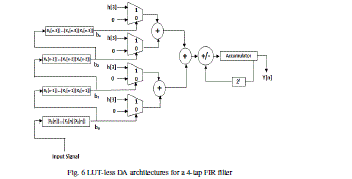Fig. 6 LUT-less DA architectures for a 4-tap FIR filter

FINAL BLOCK DIAGRAM OF 31-TAB FIR FILTER

Above block diagram shows the final block diagram of the 31 – Tab FIR Filter. In this diagram consist of PISO shift register, where PISO means parallel in and serial out that mean shift Register received data in parallel form and give out put in serial form. It is also consist of 8 types of 4 – Tab FIR Filter. For this purpose no. of 8 LUT’s used. It is modified LUT of basic LUT. It is connected between the pipeline register and shift register. When pipeline register use as element, which increase the system speed. LUT – 0 and LUT – 1 are connected to the adder similarly all the no. of 6 LUT’s are connected to the adder in coupling form after that the adding separate result of 4 LUT’s are connected to the individual adder and finally both adding result add by the final adder. Final result of the entire adding is saved to the accumulator.

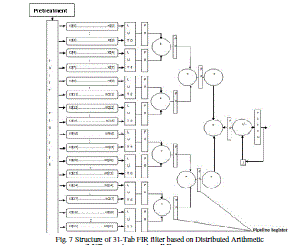Fig. 7 Structure of 31-Tab FIR filter based on Distributed Arithmetic (LUT – Look Up Table, P.R. – Pipeline Register)

SIMULATION RESULT OF BASIC LUT

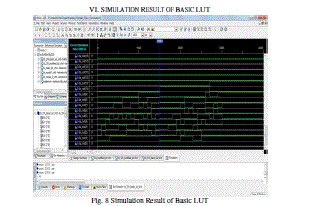Fig. 8 Simulation Result of Basic LUT

SIMULATION RESULT OF MODIFIED LUT

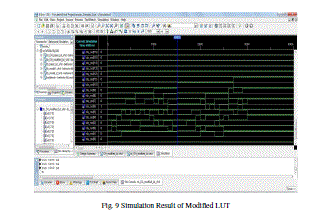DESIGN SUMMARY OF BASIC LUT

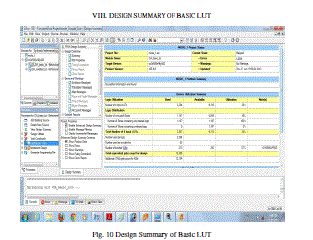Fig. 10 Design Summary of Basic LUT

DESIGN SUMMARY OF MODIFIED LUT

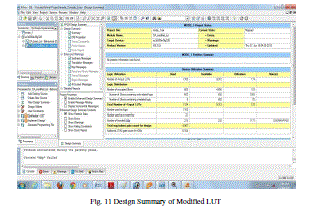Fig. 11 Design Summary of Modified LUT

SYNTHESIZE OF BASIC LUT

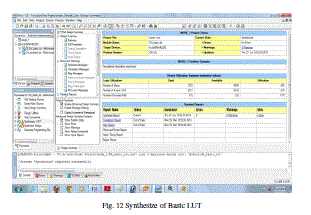Fig. 12 Synthesize of Basic LUT

SYNTHESIZE OF MODIFIED LUT

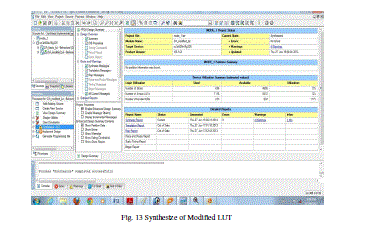Fig. 13 Synthesize of Modified LUT

RTL SCHEMATIC MODEL OF MODIFIED LUT

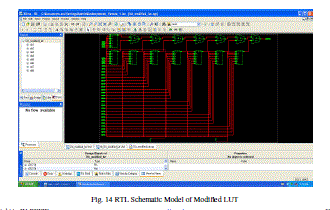Fig. 14 RTL Schematic Model of Modified LUT

CONCLUSION

This reports the proposed DA architectures for high-order filter. The architectures reduce the memory usage by half at every iteration of LUT reduction at the cost of the limited decrease of the system frequency. We also divide the highorder filters into several groups of small filters; hence we can reduce the LUT size also. As to get the high speed implementation of FIR filters, a full-parallel version of the DA architecture is adopted. We have successfully implemented a high-efficient 31-tap full-parallel DA filter, using both an original DA architecture and a modified DA architecture on a 4VLX40FF668 FPGA device. It shows that the proposed DA architectures are hardware efficient for FPGA implementation. the design and implementation based on Distributed Arithmetic, which is used to realize a 31- order FIR low-pass filter. Distributed Arithmetic structure is used to increase the recourse usage while pipeline structure is used to increase the system speed. The test results indicate that the designed filter using Distributed Arithmetic can work stable with high speed and can save almost 50 percent hardware recourses. Meanwhile, it is very easy to transplant the filter to other applications through modifying the order parameter or bit width and other parameters, and therefore have great practical applications in digit signal processing. After all implementation and simulation result of the basic LUT and modified LUT result .according to Fig. 8 and Fig. 9 these are the diagram of Basic LUT and modified LUT . these wave from result are same that mean basic LUT work with large memory space and modified LUT work with small memory space so that wave result of both LUTs are same. After that according to the design summary result, we take Fig. 10 and Fig. 11. These are the diagrams of Basic LUT and modified LUT. Now take the device utilization summary of Basic LUT.

Now we take the device utilization summary of modified LUT.

TABLE III

Device utilization Summary of Modified LUT

After that compare both device utilization summary of basic LUT and modified LUT in the Basic LUT the utilization of No. of slice is 26%. But in the modified LUT it is 13% and 386/4656 the ratio of utilization is 1233/4656. Similarly in the basic LUT the utilization of no. of 4i/p LUTs is 23% but in the modified LUT it is 12% and the ratio of utilization is 759/9312. But No. of banded IOB’s ratio of utilization 273/232 is common both LUT’s and utilization percentage is 117% it is also common in both the LUT.

FUTURE WORK

Till now all the DA based adaptive filter was implemented in an ordinary look up table so the development here is constructing the look up table in efficient manner that is Distributed arithmetic by offset binary coding. In this off set binary coding, the look up table is exactly reduced by half from the actual look up table. Divided LUT method is used to decrease the required memory units or reduced the circuit scale and pipeline structure is also used to increase the system speed. It is also useful for where FIR filter is used in digital signal processing. The basic LUT use in this paper that can reduced in 3 time that mean we can decrease the circuit scale and increase the system speed in 3 time such that there are many FIR filter based DSP application where this method can use and we can do decrease the circuit scale as well as increase the system speed so it is main FUTURE WORK of this paper. It is very easy to transplant the filter to other applications through modifying the order parameter or bit width and other parameters, and therefore have great practical applications in digit signal processing. So this is somewhat area efficient filter based on look up table, named as Distributed Arithmetic for FIR filter.

ACKNOWLADGEMENT

I thank all Department of Electronic and communication faculty members of Oriental University Indore, Staff, who have helped me in many ways directly or indirectly for this paper. I would like to dedicate this paper to my family and friends and to God, who gave me support during the tough times in the course of completion of the paper.

References

Uwe Meyer-Baese.Digital signal processing with FPGA[M]. Beijing: Tsinghua University Press, 2006.
Tsao Y C and Choi K. Area-Efficient Parallel FIR Digital Filter Structures for Symmetric Convolutions Based on Fast FIR Algorithm [J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems,,PP(99),2010.
Stanley A. White, “Applications of distributed arithmetic to digital signal processing: A tutorial review,” IEEE ASSP Magazine, vol. 6, pp. 4–19, July 1989.
S. Haykin, Adaptive Filter Theory, Prentice Hall, Upper Saddle River, NJ, 1996.
C. F. N. Cowan and J. Mavor, “New digital-adaptive filter implementation using distributed-arithmetic techniques,” IEE Proceedings, vol. 128, Pt. F, no. 4, pp. 225–230, August 1981.
A. Peled and B. Lie, “A new hardware realization of digital filters,” IEEE Transactions on A.S.S.P., vol. 22, pp. 456–462, December 1974.
Partrick Longa, Ali Miri, "Area-Efficient Fir Filter Design on FPGAs using Distributed Arithmetic" IEEE International Symposium on Signal Processing and Information Technology, pp:248-252,2006.
Sangyun Hwang, Gunhee Han,Sungho Kang, Jaeseok Kim, "New Distributed Arithmetic Algorithm for Low-Power FIR Filter Implementation", IEEE Signal Processing Letters, Vol.11, No5, pp:463-466,May, 2004.
Heejong Yoo, David V.Anderson, "Hardware-Efficient Distributed Arithmetic Architecture For High-order Digital Filters", IEEE International Conference on Acoustics, Speech and Signal Processing, Vol.5,pp. 125-128,March,2005.
Wangdian, Xingwang Zhuo "Digital Systems Applications and Design Based On Verilog HDL", Beijin: National Defence Industry press, 2006.
McClellan , J.H. Parks, T.W. Rabiner, L.R. "A computer program for designing optimum FIR linear phase digital filters":. IEEE Trans. Audio Electroacoust. Vol. 21, No.6, pp:506-526, 1973.
M. Keerthi 1, Vasujadevi Midasala2, S Nagakishore Bhavanam3, Jeevan Reddy ``FPGA Implementation of Distributed Arithmetic For FIR Filter” International Journal of Engineering Research & Technology (IJERT), Vol. 1 Issue 9, November- 2012.
Yajun Zhou, Pingzheng Shi “Distributed Arithmetic for FIR Filter implementation on FPGA’’ IEEE International Conference on Multimedia Technology, Print ISBN: 978-1-61284-771-9, pp. 294 - 297, july 2011.