Design and Implementation of High Performance Adaptive FIR Filter Systems Using QRD-RLS Method

Chaitra N; Mr. Praveen Kumar Y G; Dr. M Z Kurian

Design and Implementation of High Performance Adaptive FIR Filter Systems Using QRD-RLS Method

Chaitra N¹, Mr. Praveen Kumar Y G², Dr. M Z Kurian³

PG Student [DE], Dept. of ECE, SSIT, Tumkur, Karnataka, India
Assistant professor, Dept. of ECE, SSIT, Tumkur, Karnataka, India
HOD, Dept. of ECE, SSIT, Tumkur, Karnataka, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, an adaptive FIR filter hardware architecture with high performance is designed. The RLS (Recursive Least Square) algorithm for adaptive signal processing is explored based on QR decomposition, which uses Givens Rotation algorithm. The Givens Rotation algorithm will be implemented using CORDIC algorithm. This design is suitable for high-speed FPGAs or ASIC design. This QR Design is tested using Xilinx-FPGA as a case study

Keywords

Adaptive Filter, CORDIC method, Givens Rotation method, QR-Decomposition, RLS algorithm.

I.INTRODUCTION

Adaptive filtering techniques can be used in many applications in different fields, such as wireless communication, signal de-noising, sonar signal processing, clutter rejection in radars, and channel equalization, noise cancelling techniques, channel estimation and medical signal processing. An adaptive filter can be operated in different environmental conditions which are not known. They can automatically adapt to the face of changing system requirements and changing environments. The estimated error controls the adjustable filter coefficients of adaptive filter and with the help of input signal and desired response the further computation can be performed. Using some updated equations they can be trained to perform specific filtering and decision-making tasks. To make a useful filter the adaptive filter uses this feature for various applications of signal processing and control. In some applications adaptive filter can be used in which where some parameters are not known in advance. It uses feedback in form of error signal generated by the filter output and to adjust its transfer function to match the changing parameter it uses noise corrupted signal. This error is minimized by updating the coefficients of a digital filter according to an appropriate algorithm for specific applications.

The adaptive filtering implementation is very complex, hence it uses standard RLS algorithm which requires a direct matrix inversion operation which may cause numeric stability problems. Later QR decomposition with back substitution method is able to solve this issue. The newly designed method called QR Decomposition Recursive Least Square (QRD-RLS) offers the most robust numerical properties and hardware specific accelerator architecture compared to last two methods.

Hence in this paper QRD-RLS algorithm has been proposed. QRD-RLS algorithm uses highly efficient hardware architecture. This algorithm has wide applications in wireless communications and signal processing such as beam forming, channel equalization and HDTV. QRD-RLS has rapid convergence and is numerically stable. It also involves local communication between nodes which is suitable for hardware implementation and the hardware optimization. QRD has different types of algorithms; the one used here is CORDIC methods. For fixed-point calculations a very suitable rotation algorithm is CORDIC (Coordinate Rotation Digital Computer). For calculating trigonometric functions such as sine and cosine it is called as iterative algorithm.

II.RELATED WORK

Joseph B. Evans, “Efficient FIR Filter Architectures Suitable for FPGA Implementation”(1). In this paper efficient architecture for FIR filters will be discussed here. By exploiting the reduced complexity made possible by the use of two powers-of-two coefficients, these architectures allow the implementation of high sampling rate filters of significant length on a single field-programmable gate array (FPGA). In order to attain high performance, parallel implementation strategies such as systolic methods have been applied. Word-parallel, bit-parallel processing techniques appear to scale well with improvements in implementation technology and increasing demands for higher performance. A new parallel FIR filter building blocks suited for implementing filters where each of the coefficient values is a sum or difference of two power-of-two terms is presented and architecture allow high sampling rate in this design.

G.L. Bernocchi, G.C. Cardarilli, A. Del Re, A. Nannarelli and M. Re, “A Hybrid RNS Adaptive Filter for Channel Equalization” (2). In this paper a hybrid Residue Number System (RNS) implementation of an adaptive FIR filter is designed. The adaptation algorithm used is the Least Mean Squares (LMS). The filter has been designed to meet the constraints of specific class of applications. In fact, it is suitable for applications requiring a large number of taps where a serial updating of the filter coefficients is feasible. The RNS implementation of FIR filters grants earnings in area ad power consumption due to the introduced arithmetic simplifications has been shown in literature.

Bijan Sayyarrodsari, Member, IEEE, Jonathan P. How, Babak Hassibi, and Alain, “Estimation-Based Synthesis of H∞ –Optimal Adaptive FIR Filters for Filtered-LMS Problems”(3). A systematic synthesis procedure for H∞-optimal adaptive FIR filters in the context of an active noise cancellation (ANC) problem is discussed here. An estimation interpretation of the adaptive control problem is introduced first. Based on this interpretation, an estimation problem is formulated, and its filtering solution is discussed. The solution minimizes the maximum energy gain from the disturbances to the predicted estimation error and serves as the adaptation criterion for the weight vector in the adaptive FIR filter. This adaptation scheme is referred as estimation-based adaptive filtering (EBAF). Here steady-state gain vector in the EBAF algorithm approaches that of the classical filtered- X LMS algorithm. The error terms, however, are shown to be different. Comparisons to the results from conventional filtered-LMS algorithm show faster convergence without compromising steady-state performance and robustness of the algorithm to feedback contamination of the reference signal. Finally, more efficient implementation schemes can further reduce computational complexity of the algorithm.

M. M.Sheikh Algunaidi1, M. A. Mohd Ali1 and Md. Fokhrul Islam2*, “Comparative analysis of fetal electrocardiogram (ECG) extraction techniques using system simulation” (4). A system simulation to compare between two adaptive filters based on recursive least square (RLS) and normalized least mean square (NLMS) is modelled, in their use for fetal heart rate (FHR) monitoring. The reference and primary signals are fed simultaneously to the inputs of the RLS and NLMS adaptive filters to extract the fetal signal. Each extracted signal is post processed using a newly developed enhancement technique. At the end RLS will give high output compared with NLMS. The average values of sensitivity and positive prediction of the RLS based method are compared to NLMS based method. Finally the RLS ANC technique gives better results to be used in realizing FHR monitoring.

Marjan Karkooti, Joseph R. Cavallaro,“FPGA Implementation of Matrix Inversion Using QRD-RLS Algorithm” (5). A novel architecture for matrix inversion by generalizing the QR decomposition-based recursive least square (RLS) algorithm is designed here. The use of Squared Givens rotations and a folded systolic array makes this architecture very suitable for FPGA implementation. Input is a 4*4 matrix of complex, floating point values. The matrix inversion design can achieve throughput of 0:13M updates per second on a state of the art Xilinx Virtex4 FPGA running at 115MHz. Due to the modular partitioning and interfacing between multiple Boundary and Internal processing units, this architecture is easily extendable for other matrix sizes. In this work, architecture for matrix inversion by generalizing the QR decomposition-based Recursive Least Square algorithm (QRD-RLS) is developed.

Walter G. Huang, “Implementation of Adaptive Digital FIR and Reprogrammable Mixed-Signal Filters Using Distributed Arithmetic” (6).The typical computational flow of distributed arithmetic for adaptive filtering requires a significant increase in the computational workload over the non-adaptive case and a noticeable increase in the computational time when constrained with limited computing resources. These additional resources are needed for updating the contents of the memory table associated with distributed arithmetic. For these applications, one of the typical advantages of distributed arithmetic that is the low computing requirement is significantly diminished or eliminated. Although these approaches do reduce the amount of processing necessary to update the memory, this reduction is gained at the expense of additional memory usage and of convergence speed. To address these issues, a new type of adaptive distributed arithmetic filter is proposed.

II.SYSTEM MODEL AND ASSUMPTIONS

Systems design is the process of defining the architecture, components, modules, interfaces, and data for a system to satisfy specified requirements. In this section, details for the system design are given to satisfy the requirements for implementation.

The structure of a classical adaptive filtering system is shown in Figure 1. The input signal is given to FIR filter design; the output signal of FIR is added with a noise or reference signal. Then this error signal is given to QRDRLS adaptive algorithm for estimation of filter coefficients. The two popular methods in implementation of QR Decomposition-based are CORDIC method and LUT-N method. Performance comparison can be done for these two methods to get highly efficient output. The output of algorithm is again given to FIR filter design. This design will remove the error signal by using filter coefficients and the filtered output is obtained at the output signal.

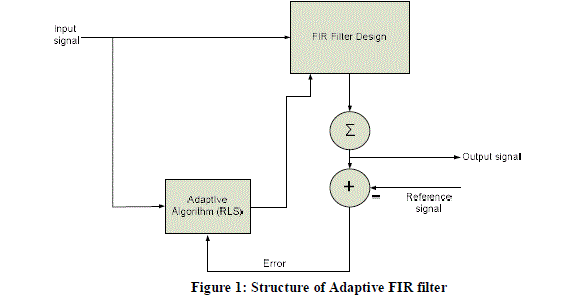The complexity of a standard RLS algorithm requires O (N2) operations per sampling period, including multiplications and divisions, where N is the number of taps in the adaptive filter. Also, numerical overflow limits RLS applications. The implementation of basic FIR filter is described in this section. FIR filters has great advantages in terms of area, speed and power consumption. This module is used in digital signal processing by virtue of its stability and easy implementation whenever required. Using verilog HDL this FIR filter module is implemented.

III.PROPOSED METHODOLOGY AND DISCUSSION

The first block in the structure of adaptive FIR filter is FIR filter design. The multiplications can be implemented through the adder circuit tree by sharing partial results that implement the multiple constant multiplications (MCM) block. The MCM block, shown in Figure 2, is the combinational hardware architecture which implements all the filter multipliers simultaneously. Here the shift-add multiplier circuits are used in order to optimize the filter architectures. An adder must be used in order to provide the partial product terms in this design. D-FF is used as shifter and storage device here.

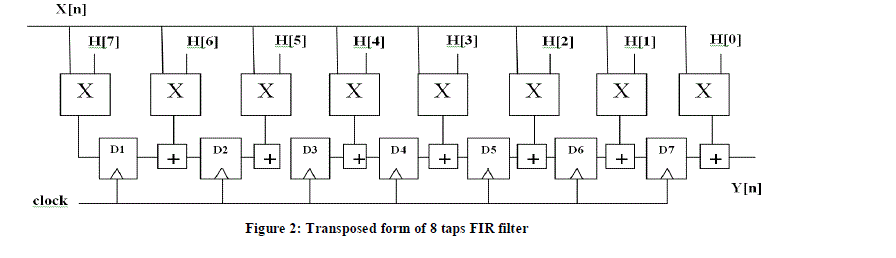The next block in the structure is an adaptive algorithm .Here the filter is aimed at reducing noise or any other undesired signals from the input signal. The adaptive algorithm estimates weight adjustments to obtain the FIR filter coefficients by minimizing the error signal. The popular methods for estimation of filter coefficients are the RLS and LMS algorithms. Adaptive filtering using the RLS algorithm gives better performance compared with the NLMS and LMS algorithm due to faster convergence and smaller final error. Since, the complexity of a standard RLS algorithm requires O (N2) operations per sampling period, including multiplications and divisions, where N is the number of taps in the adaptive filter. Also, numerical overflow limits RLS applications. The QRD-RLS algorithm also provides relations for avoiding overflow and equations for the mean squared values of the internal variables in the algorithm. QR decomposition has better and more robust numeric properties than other methods. Based on the previous work, mapping of QR decomposition algorithm to the VLSI and FPGA platform with good performance is possible compared with conventional designs.

The different methods can be implemented using QR Decomposition. For square root operation the CORDIC algorithm is the better one and is illustrated in Figure 3.

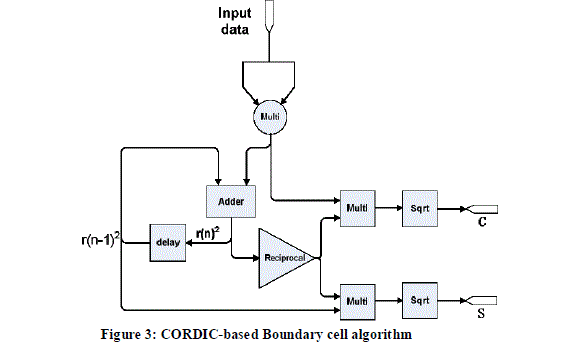The CORDIC methods use some of the arithmetic blocks for its operations. In this paper a ripple carry adder is used. A ripple carry adder is a digital circuit that gives the arithmetic sum of two binary numbers. It can be designed with cascading required number of full adders; with the carry output from each full adder connected to the carry input of the next full adder in the cascade. The multiplier is an important block of digital signal processors. Because of the circuit complexity, the power consumption and area are the two important design considerations of the multiplier. In this paper a low power multiplier is used which aims at low area architecture for the shift and add multiplier.

IV.EXPERIMENTAL RESULTS

When the clock is high and reset is low, the output will be obtained at data out pin. Here input is of 8bit data used to get 16bit output data, order of the filter is 7. Using FDA Tool in mat lab, an 8 coefficients using Low pass FIR based on least square method is designed. The input and outputs relations are analysed in Table 1.

The simulation result for basic FIR filter is as shown in Figure 4. It gives the complete output for basic FIR filter with 8taps. In this basic FIR filter an adder and low power multiplier is used. An 8 tap filter is designed here, after 8 multiplications, adds and shift operations the output is obtained at the final block.

The Cordic algorithm is a combination of shift-add operations, and multiplications are not required. The input and outputs are analysed for figure 7 is shown in below Table 2. When the below specified inputs are given the output of final block yields C and S values.

The simulation result of Cordic method is as shown in Figure 5. . The reset should be made low to get the output, then control, clock, load inputs should be applied. Then load should be made low to get the final simulation output of Cordic method. Finally this output will generate desired input as filter coefficients which help in removal of error signal in filter.

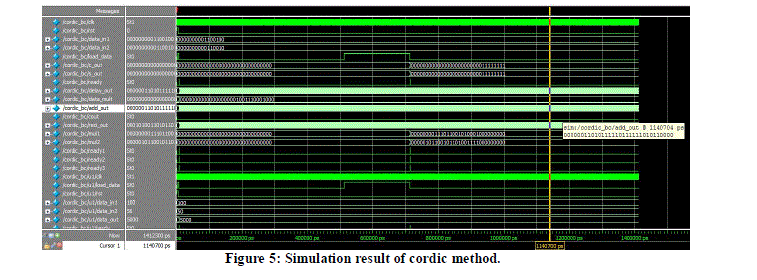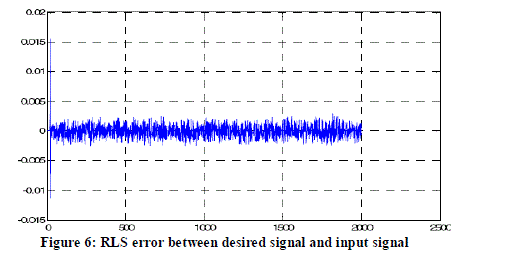
The error output between the estimated signal and desired signal is less than 0.025%as shown in below Figure 6. The QRDRLS simulation gives better estimation performance and it also verifies the QR factorization implementation.

V.CONCLUSION

In this paper, an improved CORDIC based boundary cell architecture method is for the QRD-RLS algorithm based on hardware implementation. The error of the CORDIC method is reasonable and acceptable for high-speed adaptive signal processing. The CORDIC based architecture results in hardware with about twice the area and more than 50% more latency compared to the Givens rotation based architecture.The optimized hardware allows the CORDIC based algorithm running at higher throughput.

References

Joseph B. Evans, “Efficient FIR Filter Architectures Suitable for FPGA Implementation”, Prentice Hall, 2009.
G.L. Bernocchi, G.C. Cardarilli, A. Del Re, A. Nannarelli. and M. Re, “A Hybrid RNS Adaptive Filter for Channel Equalization”, Prentice- Hall. 2006.
Bijan Sayyarrodsari, Member, IEEE, Jonathan P. How, Babak Hassibi, and Alain, “Estimation-Based Synthesis of H∞ –Optimal Adaptive FIR Filters for Filtered-LMS Problems”, 2001.
M. M. Sheikh Algunaidi1, M. A. Mohd Ali1 and Md. Fokhrul Islam2*, “Comparative analysis of fetal electrocardiogram (ECG) extraction techniques using system simulation”, 2011.
Marjan Karkooti, Joseph R. Cavallaro, “FPGA Implementation of Matrix Inversion Using QRD-RLS Algorithm”, 1892.
Walter G. Huang, “Implementation of Adaptive Digital FIR and Reprogrammable Mixed-Signal Filters Using Distributed Arithmetic”, December 2009.
Chang-Seok CHOI†a), Nonmember and Hanho LEE†b), “A Self-Reconfigurable Adaptive FIR Filter System on Partial Reconfiguration Platform”, 2007.
B. Widrow and S.D. Stearns, “Adaptive Signal Processing”, Prentice Hall, 1985.
Cioffi, J.M., “The Fast Adaptive ROTOR's RLS Algorithm”, Acoustics, Speech and Signal Processing, IEEE Transactions on, vol.38, no.4, pp.631-653, Apr 1990.
Aslan, S. Niu, S. Saniie, J. , "FPGA Implementation of Fast QR Decomposition Based on Givens Rotation," Circuits and Systems (MWSCAS), 2012 IEEE 55th International Midwest Symposium on , vol., no., pp.470-473, 5-8 Aug. 2012.