Design and Simulation of MEMS Comb
Vibratory Gyroscope

S.Yuvaraj; V.S.Krushnasamy

Design and Simulation of MEMS Comb Vibratory Gyroscope

S.Yuvaraj¹, V.S.Krushnasamy²

PG Student, Dept. of ICE, SRM University, Chennai, Tamil Nadu, India
Assistant professor,Dept.of ICE, SRM University,Chennai,Tamil Nadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

MEMS is (Micro Electro Mechanical Systems) refer to device or systemthat’s integrated with electrical and mechanical modules in the scale of microns. It is low power consumption, very small in size, very low price, and high efficiency in nature. In this study a novel comb-drive, variance capacitance detecting gyroscope is actuated to vibrate along X-axis by electrostatic comb driving. If the angular velocity along Y-directions is expert, theCoriolises force actuates the central proof mass along Z-directions. The size of the driving beams and sensing beams are sensibly chosen to reducing the frequency mismatch in two directions, thus increasing the sensitivity of gyroscope. Intellisuite simulation is used to find out the device frequency and displacement. Gyroscope is most commonly used in inertial navigation, automobile, aerospace ship, consumer products, micro satellite, etc

Keywords

Tuning fork, Comb vibratory gyroscope, MEMS (Micro Electro Mechanical Systems), Intellisuite.

I.INTRODUCTION

MEMSis normallyconsidered as devices and systems integrated with mechanical elements, actuators, sensors and electronic circuits on a common silicon substrate through micro fabrication technology [3]. MEMS are made up of components value between 1 to 10000 micro meters in size (i.e. 0.0001 to 0.1 micrometre). They are generally consisting of theessential unit that processes data, the several components like that microcontroller that are related with the outside such as micro sensors and micro actuators. Gyroscopes are extra category that denotes MEMS inertial sensors. Conventional (non MEMS) spinning wheel gyroscope are common, but raising and turning of a MEMS device with no springs has not yet been commercialized. Many MEMS type of gyroscopes have been did in the literature work, with most subsiding into the sets of tuning fork gyroscopes [7], fluctuating wheels, lavender glass resonators and Foucault swings.

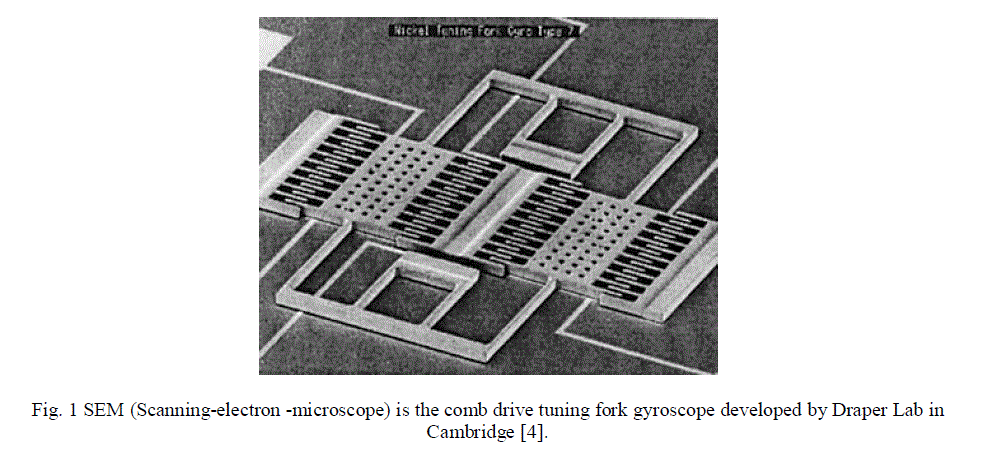The tuning fork gyroscopes have a pair of masses that are motivated to fluctuate with equal amplitude but in reverse directions. When we rotated, the Coriolis force creates an orthogonal vibration that can be sensed by a variation of devices.The normal gyroscope shown in fig1 is using the comb type structures to drive the tuning-fork into resonance [6]. The gyroscope has the several type of the technique is based upon variant structure. Like that scanning electron microscope structure has the view of comb drive double folded beam structure is obtained the sensitivity of the device [5].

II.LITERATURE REVIEW

A. Sharma,etc al [4]This paper presents the design and implementation of an in-plane solid-mass single-crystal silicon tuning fork gyro that has the potential of attaining sub-deg/hr rate resolutions. A design is devised to achieve high Q in the drive and sense resonant modes (Qdrive=81,000 and Qsense=64,000) with effective mode decoupling. The gyroscope was fabricated on 40μm thick Silicon-on-Insulator (SOI) using a simple two-mask process. The drive and sense resonant modes were balanced electrostatically to within 0.07% of each other and the measured rate results show a sensitivity of 1.25mV/º/s in a bandwidth of 12Hz.

X. Xiong, etc al [3]In this paper, a novel DRIE (Deep Reactive Ion Etching) bulk micro machined single-crystal silicon comb vibratory micro gyroscope is introduced. The device uses glasses substrate so that parasitic capacitance can be alleviated. Due to DRIE technique the device thickness can be increased to be more than 100μm. The working principle of the micro gyroscope is introduced. The dynamics analysis of the gyroscope is also performed. Based upon the analysis, an optimized micro gyroscope design is proposed. The designed gyroscope is expected to have a sensitivity of 4ÃÂ¯ÃÂÃÂV/(°/sec).

Xuesong Jiang, etc al [5] A monolithic surface micro machined Z-axis vibratory rate gyroscope with an on-chip A/D converter is fabricated in a monolithic MEMS/circuits technology with 2ÃÂ¯ÃÂÃÂ°ÃÂ¯ÃÂÃÂ CMOS and 2.25ÃÂ¯ÃÂÃÂm-thick mechanical polysilicon. The on-chip position sense circuit uses correlated double sampling to reject l/f and kT/C noise and resolves 0.02Angstrom displacements. The gyroscope achieves a sensitivity of 3ÃÂ¯ÃÂÃÂV/°sec/.\IHz at atmospheric pressure and operates from a single 5V supply.

Z.Y. Guo, Z, etc al [6]A decoupled lateral-axis TFG (tuning fork gyroscope) with novel driving and sensing combs is presented. The EFBD (electrostatic force balanced comb driver) adopted in the TFG can efficiently suppress the mechanical coupling in a simple manner. The structure of the gyroscope is also optimized to suppress the coupling further. Moreover, torsional sensing combs are adopted to detect the out-of-plane movement, so it can work at atmospheric pressure. The TFG was fabricated and tested at atmosphere. The measured CFDTS (coupling from driving mode to sensing mode) and CFSTD (coupling from sensing mode to driving mode) are -45dB and -51dB respectively. The sensitivity is 2.9mV/°/s while the nonlinearity is 0.9% with the full scale of 800°/s. The noise floor is 0.035°/s/Hz1/2.

III.PROPOSED WORK

Working Principle of Gyroscope: A vibratory gyroscope normally has two upright vibration modes are driving mode and sensing mode, which can be easy as a mass suspended by springs along two orthogonal axis [1], as shown in fig 2.

When the mass is driven along the x direction by an outside force (F(t)=F0cosÃÂ¯ÃÂÃÂ·dt), and it is subjected to a constant angular velocity (Ω), a Coriolis force is induced in y-direction. In this case, the equation of movement is.

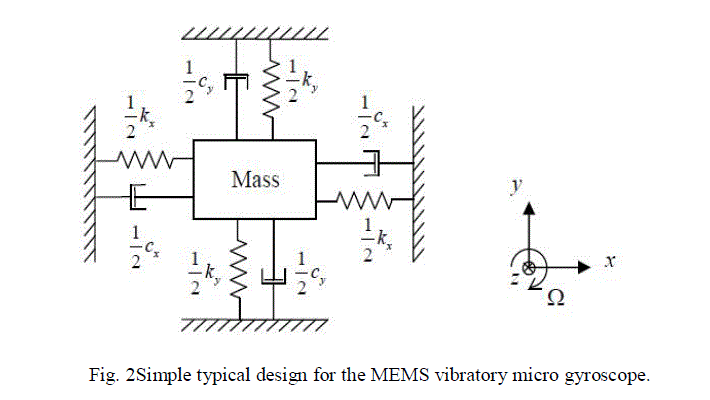Where m is the mass, cxand cyare the air damping coefficients,kxand kyare the spring constants of the driving beam and the sensing beam on x and y direction respectively,x(t) and y(t) are the displacement of the central mass on x and y direction respectively. Solving the above differential equations, we can have oscillatory motion in x and y direction.

When resonant frequency in x direction and y direction is precisely matched, which means θ = 0, the mass oscillates along a linear path at an angle to the x-axis, as shown in fig 3.

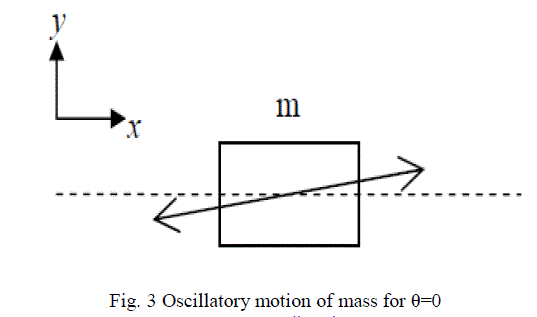Fig 4 shows the relationship between the normalized sensitivity sdn and (ωx / ωy) for different Qy values [3].

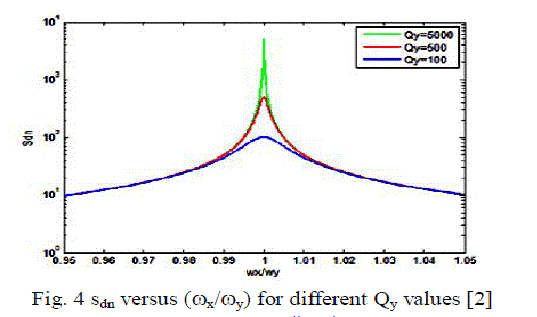(ωx / ωy) = 1From the curves we can see that the displacement sensitivity takes its peak value, which shows that in order to confirm the high sensitivity, we need to surely match the resonant frequencies of driving and sensing mode. With the increase of Qy, the peak becomes narrower and sharper, which specify that increasing quality factors is another way to increase sensitivity [9].

IV.SIMULATION

The structure is analysed by using the SYNPLE module of intellisuite a commercial finite element analysis package. In this analysis, structural mechanical model is used for computing the gyroscope. The coriolis force, that governs the device, is applied as the boundary load [8].

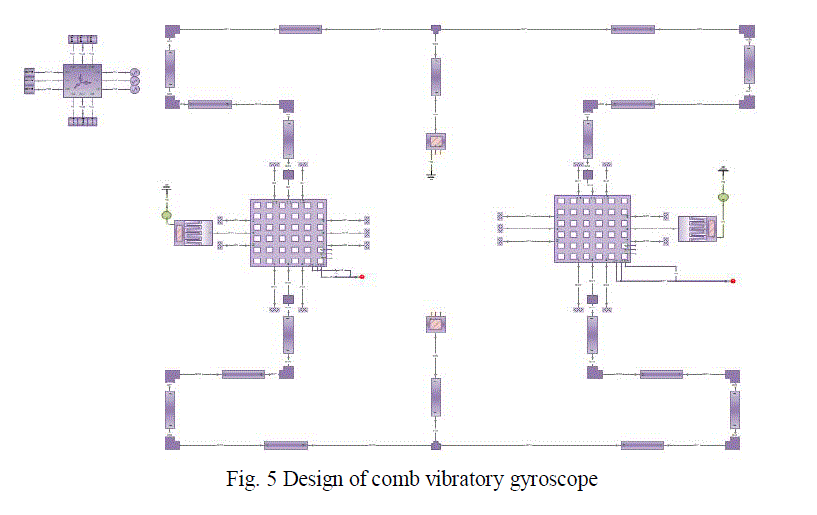The device is initially operated at its natural frequency. The frequency range applied is 1 KHz to 10KHz. The device is electrostatically and mechanically meshed to generate a finer mesh. The electrostatic mesh is used at the comb drives, since they are electrostatic elements. The mechanical mesh is applied for the spring support.

The device is subjected to static frequency analysis. In this analysis, the device is actuated by applying voltage to the comb drives. The simulation takes few minutes. Both of the masses of the gyroscope will move inX-direction. The mode 3 will be the drive mode of the device because the proof masses will vibrate in X-direction with a phase shift. When coriolis force is applied in Z-direction perpendicular to the applied force of the mode 2 is the sense mode of the device.

V.RESULTS

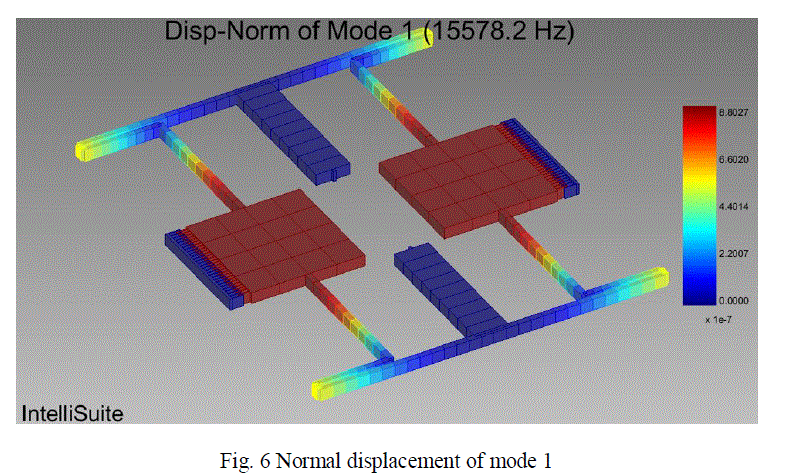
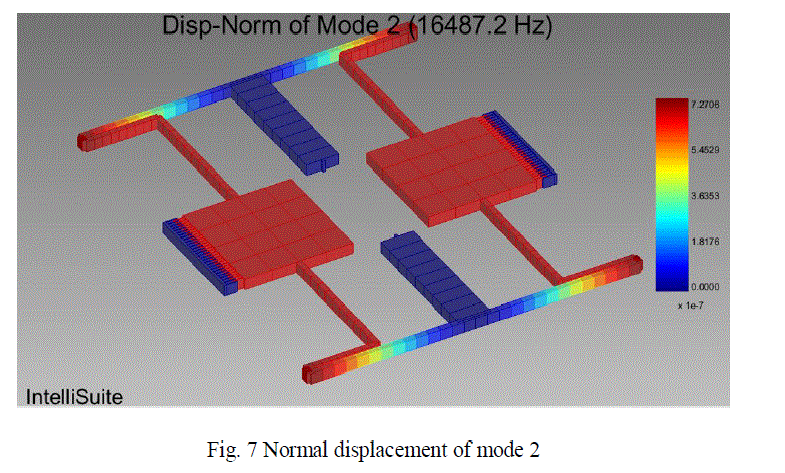
MEMS 3D Visualization module: Using 3D visualization module various modes of displacement is analysed. The fig 6, 7 and 8 shows that normal displacement of the device at its mode 1, mode 2 and mode 3.

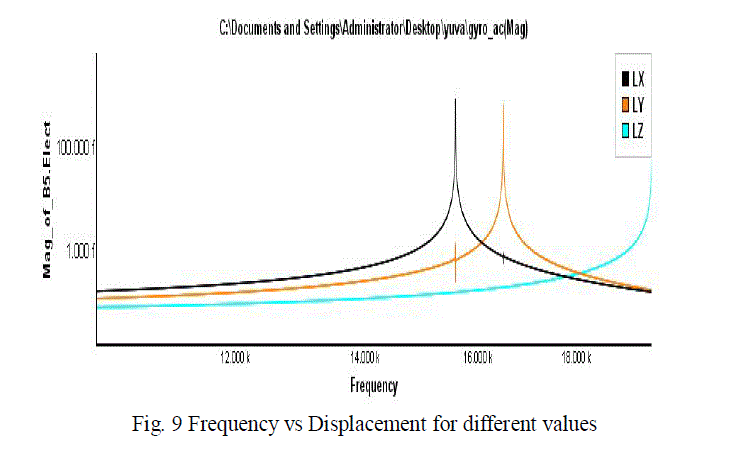
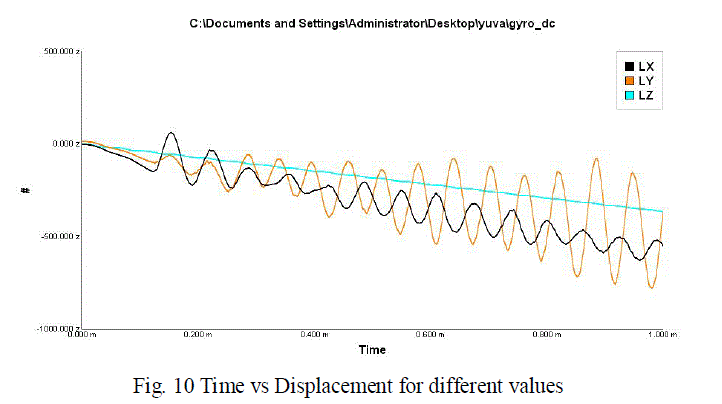
From the figure it can be seen that the device vibrates at its drive mode at a frequency of 15578.2Hz, 16487.2Hz and 19678.2Hz. Figure 9 and 10 shows that the displacement for the various frequencies and time.

The transient response of the device is achieved on applying the force. From fig 11, 12 and 13 it is observed that the transient response has a phase shift in both X & Y-direction. This is because on applying the coriolis force, the proof mass gets displaced with same magnitude but in opposite direction.

The simulation of AC Analysis: Initialize the AC simulation and the frequency value is assigned in such a way to so that the small signal analysis can be performed frequency=1k. The X, Y and Z displacement of the two proof masses will be observed. after a minute the message window informing about the location of the simulation results. Using the 2D graph to view the output signals

Transient Simulation Analysis: The AC voltage loads have been applied to the comb drives and the simulation is set up to run for the 10 millisecond with a time step of 1 microsecond. After the simulation completed we can get the graph of transient response.

Dc Simulation Analysis: The 100 V DC voltage loads have been applied to the comb drives. To run the simulation you will see the proof mass displacement 0.808 microns in X-direction, 0.72 microns in Y-direction and 1.012 microns in Z-direction.

VI.CONCLUSION

MEMS based comb vibratory gyroscope was designed and analysed using Intellisuite software in SYNPEL and 3D module. The displacement and rotation for X, Y and Z direction using AC, DC analysis is obtained and transient analysis for frequency and time was simulated. The graphical representation for frequency vs displacement and time vs displacement was studied. MEMS 3D Visualization the normal displacement of X-direction is 0.808μm (/0s) at the frequency of 15578.2Hz. The normal displacement of Y-direction is 0.72μm (/0s) at the frequency of 16487.3Hz. The normal displacement of Z-direction is 1.012μm (/0s) at the frequency of 19678.2Hz.

References

H. Dong, X. Xiong, "Design and Analysis of a MEMS Comb Vibratory Gyroscope", American Society for Engineering Education Northeast Conference, Apr. 3-4, 2009.
K. Tanaka, Y. Mochida, M. Sugimoto, K. Moriya, T. Hasegawa, K. Atsuchi and K. Ohwada, "A Micromachined Vibrating Gyroscope", Sensors & Actuators A: physical, Vol. 50, pp.111-115, 1995.
X. Xiong, D. Lu and W. Wang, "A Bulk-micromachined Comb Vibrating Microgyroscope Design", the 48th IEEE International Midwest Symposium on Circuits & Systems, Vol.1, pp. 151-154, Aug 7-10, 2005.
A. Sharma, F. Zaman, B. Amini and F. Ayazi, "A High-Q In-Plane SOI Tuning Fork Gyroscope", Proceedings of IEEE Volume , Sensors, Vol.1 Oct. 24-27, PP. 467-470, 2004.
W. Clark, R. Howe, and R. Horowitz, "Surface Micromachined Z-axis Vibratory Rate Gyroscope", IEEE Proceedings on Solid-state Sensors and Actuators, Hilton Head Island, SC, USA, pp. 283-287, Jun. 2-6, 1996.
Z. Y. Guo, Z. C Yang, L. T. Lin, Q. C. Zhao, J. Cui, X. Z. Chi, and G. Z. Yan, “A lateral-axis micromachined tuning fork gyroscope with novel driving and sensing combs,” in Proc. Transducers Conf., Denver, pp. 288– 91, Jun. 21–29, 2009.
Y. Oh, B. Lee, S. Baek, H. Kim, J. Kim, S. Kang, C. Song, "A Tunable Vibratory Microgyroscope", Sensors & Actuators A: physical, Vol. 64, pp.51-56, 1988.
URL: http://www.intellisuite.com
URL: http://en.wikipedia.org/wiki/MEMS_gyroscope.