Design Aspects of using Low Grade Fuels to
Improve the Combustion Efficiency in Enlarge the
Free Board Zone in AFBC Boiler

Venkata Ramesh Bobba; B. Srinivas

Design Aspects of using Low Grade Fuels to Improve the Combustion Efficiency in Enlarge the Free Board Zone in AFBC Boiler

Venkata Ramesh Bobba¹, B. Srinivas ²
PG Student, Department of Mechanical Engineering, BVC Engineering College, Andhra Pradesh, India¹
Associate. Professor, Department of Mechanical Engineering, BVC Engineering College, Andhra Pradesh, India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Low grade, high ash and low calorific value of fuels can be effectively used in fluidized bed combustion; otherwise these low grade fuels are difficult to handle due to high moisture and fines content. In the present work the possibility of using Kutch lignite in the fluidized combustor to improve the combustion efficiencies are discussed. Increase in fluidized velocity along the vertical height above the distributor plate indicate that considerable burning of fuel particles is taking place in the freeboard zone rather than complete burning within the bed. Therefore, an enlarged disengagement section is provided to improve the combustion of fines. In the present work, a design of 50 TPH Coal based atmospheric fluidised bed combustion boiler in enlarge the free board zone.

Keywords

Kutch lignite, fluidized bed; free board height, free board temperature, overall heat transfer coefficients.

INTRODUCTION

A fluidized bed consists of a chamber in which solid particles are kept in a state of suspension by high velocity air forced upward through the particles. the turbulent mass of solid particles stores heat and transfers this heat rapidly to any fuel that is introduced into the bed. These results in an efficient energy conversion method, which can use a wide range of low-grade fuels. Bhattacharya et al. (1983) reported the combustion efficiency of low grade fuels in the range of 81 t0 96%. It has also been suggested that higher combustion efficiencies could be achieved by Providing an enlarged freeboard, which effectively reduces the flue gas velocity.

The fluidized velocities were varied from 0.4 to 2.2m/s with excess air levels of 30 to 95%.the bed temperature were maintained between 650 and 900OC. These results confirm that at all fluidized velocities a significant amount of combustion is taking place in the freeboard. Bhattacharya and Weizhang (1990) reported that the loss of unburnt carbon in the form of carbon mono oxide (CO) is in the order of 3 to 10%. The higher CO emissions were observed at higher fluidization velocities and this could be because of shorter residence time. Salour et al. (1993) found that the combustion efficiency in bubbling beds is dependent on the particle size of the fuel, excess air levels, bed temperature and gas velocity.

It is recommended that the height of freeboard must be increased to increase the combustion efficiencies. Kouprianov and Permchart (2003) studied the effect of operating conditions(load and excess air) as well as fuel quality and bed height on the major gaseous emissions(CO2,CO and NOx) in a fluidized bed combustor. Physico-chemical parameters in the bed i.e., minimum fluidizing velocity, bubble properties like bubble diameter, bubble rise velocity, superficial velocity of gas etc.

A.Minimum fluidization velocity:

Numbers of correlations are available in define minimum fluidization velocity, the application of which varies to a great extent depending upon the particle size in the bed. According to the equation (1) Saxean & vogal (1977) gives the best results for coarse particles.

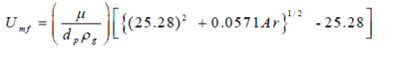Saxean & vogal (1977) correlation was used to calculate the minimum fluidization velocity in the present model because the particle size is greater than 100μm. The result of this relation is more closely matched with the larger particle size.

B. Viscosity of fluidizing gas:

Subramani et. al. (2007) gave an equation for estimating the viscosity of fluidizing air, which is a function of bed temperature only and is presented.

C.Density of fluidizing gas:

The density of fluidizing gas can be found from the work of Bird et al. (1960). The final expression for density of fluidizing gas, which is a function of bed temperature only, is presented below:

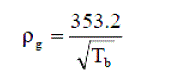D.Particle Terminal velocity:

Particle terminal velocity is also termed the particle free fall velocity or setting velocity. For a solid particle in free fall in a gas medium the terminal velocity Ut , is reaches when the downward gravitational force on the particle is equal to the upward drag force. On a gas solid medium if the upward gas velocity is large than the terminal velocity of the solid particle, the particle tends to get out of the system. Hence the determination of Ut is essential for elutriation studies. Elutriation is the process of carry over, out of the system of the Super-Fine defined as that of fraction of the bed particles whose terminal velocity is lower than the operating gas velocity. Elutriation of super fines dictates the free board height and the sizing of the downstream particulate control devices, affects the average bed particle diameter and necessitates bed material makeup to maintain overall bed performance. The following general expression can be used to determine Ut.

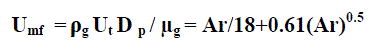When a fluidized bed is operated with gas velocities in excess of the terminal velocity of some of its constituent particles, then particles will be entrained in the freeboard and unless they are returned, the bed will be lose the material. The regime of operation above Ut is used in several particles applications and is referred to as „fast fluidizationÃÂ¢Ãâ¬ÃÅ¸, „High velocity fluidizationÃÂ¢Ãâ¬ÃÅ¸, and ÃÂ¢Ãâ¬ÃÅ¸circulating fluidizationÃÂ¢Ãâ¬ÃÅ¸.

Voidage at minimum fluidization

Observing that parameters like the bed porosity at minimum fluidization (εmf), Remf and Ar change with temperature, Subramani et. al. attempted to develop an empirical correlation to predict εmf as a function of Remf and Ar , using least square method.

For fine particles the following relation is used.

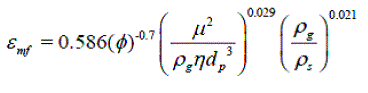For fluidization purpose the following classification can be approximated

DP > 10mm --------------- lumps

DP (1-10mm) -------------- coarse particulates

DP (500μm-1mm) --------------Fine particles

DP (50μm-500μm) --------------Powder

DP < 50μm --------------Pulverized

E.Gas distribution plate:

The distributor plate will be used as a sparger type distributor, the gas distributor plate is designed in such a way that the primary air passing through the bed in the minimum fluidization state is nearly equal to the theoretical air requires for the combustion of fuel. As the velocity of air is increased beyond the minimum fluidization state, the excess air is in the form of bubbles and the bed becomes agitated due to high solid-gas contact.

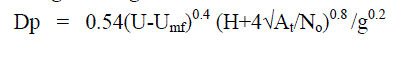F.Average equivalent bubble diameter:

Various correlations can be found in literature for the estimation of bubble diameter in a fluidized bed. One of the widely used correlations was proposed by Mori and Wen in 1975 taking into account the effect of bed diameter and distributor type on bubble diameter as follows:

For porous distributor plates.

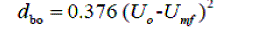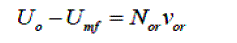Where

V or = volumetric flow rate through an orifice (m3/s);

Hence the bubble diameter just above the distributor becomes

For low gas flow rate:

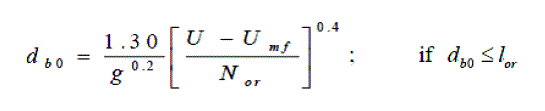Where lor = spacing between adjacent holes

Mean bubble size is depending on type of distributor, distance above the distributor plate and excess gas velocity

Pressure drop at pipe:

To measure Pressure drop across the bed and distributor.

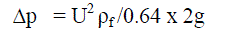G.TRANSPORT DISENGAGEMENT HEIGHT :( TDH)

The height in the bed vessel beyond which

i) Entrainment remains constant

ii) Gas flow distribution is fairly uniform

iii) Particles having Ut < Uo is called the transport dis engagement height or TDH i.e. all large particle with Ut > Uo are „disengagedÃÂ¢Ãâ¬ÃÅ¸ from the bulk of the upward flow.

The significance of the TDH lies in the fact that it is the minimum freeboard height to be provided to prevent unused sorbent particles or un burnt carbon particles.TDH determines the optimum distance for the gas exit ports above a fluidized bed TDH is determined by using the following relation

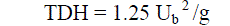Ub is the bubbling velocity in m/s

H.Expanded bed height on fluidization:

The bed expansion is governed by the following equation

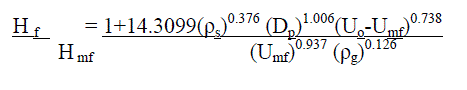Where,

Hf is the fully expanded bed height (m)

Hmf is the bed height at minimum fluidization conditions (m)

Uo is the operating superficial velocity of gas (m/s)

I. Bubble velocity:

The presence of bubbles causes the bed to expand and the prediction of bubble hold-up is possible. Using the two phase theory which states that all gas in excess of that required for incipient fluidization of the particles flows as bubbles. The absolute rise velocity of an isolated single rising bubble, ubr, was first suggested by Davidson and Harrison (1963) to be given by The motion of a single bubble in a fluidized bed can be described according to in viscid fluid equation

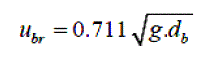Where Db is the bubble diameter

Bubble velocity is related to the bubble size through equation

Davidson and Harrison (1963) also proposed on theoretical grounds that the average absolute velocity of a crowd of bubbles in a fluidized bed may be expressed as:

Ub = bubble velocity = K(Uo-Umf)+Ubr

Where K≈1 in the region well above a distributor plate and is a function of bed voidage.

The distribution of the gas between the bubbles and dense phase is of interest because it influences the degree of chemical conversion.

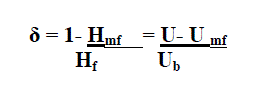The Davidson model successfully accounted for the movement of both gas and solids and the pressure distributing about rising bubbles. Davidson development a model for two and three dimensional beds (a two dimensional bed is one formed between two closely spaced parallel plates) and is based on the following postulates.

Postulate-1: A gas bubble is solid free and circular in shape and thus is spherical in the three dimensional case and cylindrical in the two dimensional case.

Postulate-2: As A bubble rises, particles move aside, as a would an incompressible in viscid fluid of bulk density δs (1-Σmf).small bubbles rise slowly and large bubbles fast.

Postulate-3: The gas flows in the emulsion phase as an incompressible viscous fluid.

Postulate-4: Series of bubbles (a train) do not have the same velocity as a single bubble.

Postulate-5: Velocity of rise of single bubbles in fluidized beds is given as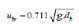

Db = diameter of bubble

Postulate-6: Gas in excess of minimum fluidization passes through as bubbles

Postulate-7: unlike in gas-liquid system there is interchange between bubble gas and emulsion gas.

Velocity of train bubbles is given as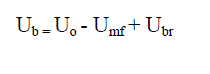

J.Bubble properties:

Considering the following patterns

Cloudness or slow bubble (Ubr< Uf = Umf/εmf):

Here the emulsion gas rises faster than bubble, hence it uses the bubble as a convenient shirt cut on its way through the bed.it enters the bottom of the bubble and leaves at the top.

However an annular ring of gas does circulate within the bubble,moving upward with it. The amount of this accompaning gas increases has the bubble velocity slows to the raise the velocity of emulsion gas. Clouded or fast bubble (Ubr> Uf ):

As with the slow bubble emulsion gas enters the lower part of the bubble and leaves at the top. However the bubble is raising faster than the emulsion gas,consequently the gas leaving the top of the bubble penetrated by this circulating gas is caled the cloud. The rest of the gas in the bed does not mix with the recirculating gas but moves aside as the fast bubble with its cloud passes.

The transition from slow to fast bubble is smooth. The cloud is infinite in thickness at Ubr = Uf but things with increasing bubble velocity.

Its size is given by

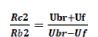for a two dimensional bed

According to Rowe and Partridge (1965), the ratio between the volumes of wake dragged upward behind a rising bubble to the volume of bubble, fw, may be taken to be roughly as 0.2.

For estimating the size of cloud, ratio of cloud volume to bubble volume (fc), the Davidson and Harrison (1963) correlation was tried.

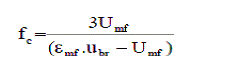The ratio of volume of cloud-wake phase to the volume of bubble fcw f is obtained as follows: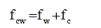

But, it was found that equation (1.27) gave absurd values of fc, for the present Case. We have therefore taken fc as an adjustable parameter, the value of which lies in between 0.025 and 0.15. This in turn implies that fcw is now an adjustable parameter, with its value varying from 0.2 to 0.4.

Flow rate of gas into and out of bubble:

This Davidson theory also shows that the upward flow of gas into and out of the bubble is

V = 3 Umf π Rb 2 = 3 Ur εmf π Rb2 for a three dimensional bed

II. OPERATING PROCEDURE

After initial start-up of the bed, the flow rate of primary air is increased till the bed reached the minimum fluidization state. the operating conditions maintained in the bed are presented in table. The theoretical air required for the combustion of fuel particles is calculated from the ultimate analysis and the excess air supplied at each flow rate and the combustion efficiency is thus calculated with the following equation:

Combustion efficiency = [Calorific value of rice straws – (Heating value of refuse at cyclone separator+ Heating value in the flue gasses)]/Calorific value of rice straws

ηc = CV-(HVR+HVG)

ηc = CV- [(Wc X CVC)+(Wco X CVCO)]

where

CV – Calorific value of fuel, Kcal/kg

CVC – Calorific value of carbon, Kcal/kg

CVCO – Calorific value of carbon monoxide, Kcal/kg

Wc - Weight of carbon in refuse, kg

Wco - Weight of carbon monoxide in flue gases, kg

INPUT PARAMETERS:

Various input parameters are taken from the plant

PROXIMATE+ULTIMATE ANALYSIS OF FUEL

III. RESULTS AND DISCUSSIONS

Effect on variation of minimum fluidising velocity with bed temperature in the combustion chamber: The variation of minimum fluidization velocity with bed temperature is show in figure 1. It is seen that as the bed temperature is increased the minimum fluidization velocity decreases. This is due to the fact that as the bed temperature is increased the resistance offered to the fluid flow is decreased because with increase in bed temperature the fluid particles get energized and they will break the intermolecular attraction forces. if we keep the other parameters same then, lesser force is required to fluidize the bed and to overcome the resistance offered to the fluid flow. Effect on variation of operating velocity with bed temperature in the combustion chamber:

In figure (2) the bed temperature is increased the operating velocity of gas increases because the operating velocity is directly proportional to the bed temperature and with in bed temperature the operating velocity also increases.Effect on variation of superficial gas velocity of bubbles with bed temperature in the combustion chamber: In figure (3) the bed temperature is increased the superficial velocity of bubbles is also increased because the superficial velocity of bubbles is directly proportional to (Uo-Umf ) and with increase in bed temperature, Uo increases and Umf decreases.Effect on variation of bubble diameter with bed height in the combustion chamber:

In figure (4) the bubble diameter is increased the bed height will also increased. Bubble diameter increases and oxygen conversion decreases with increase in bed temperature. This is due to the reason that as bed temperature increases, operating velocity increases and this will increase the bubble diameter because it is directly proportional to the operating velocity and with increase in bubble diameter.

Effect of operating conditions on combustion efficiency:

For the estimation of combustion efficiency, the heat losses owing to incomplete combustion and unburnt carbon in fly ash are determined the heat and mass balance calculation. Shows the combustion efficiency for the rice straws & rice husk fuel at maximum combustor loads for different fluidizing velocities. The maximum possible combustion efficiency for rice straws & rice husk is 95.7% at fluidizing velocity of 1.23 m/s in it can be observed that only a slight increase in combustion efficiencies is observed for rice straws & rice husk because of the low ash-fuel ratio. Even though there is a considerable reduction of carbon losses. Permchart and Kouprianov (2004) reported that for the maximum combustor load and with excess air of 50 to 100%, a combustion efficiency of over 99% could be achieved when sawdust and bagasse were fired. In the present study the maximum combustion efficiency is found to be 99.1% for 63% at excess air, which results in higher combustion efficiency at a relatively small quantity of excess air with a minimum heat loss by the exhaust gases.

The maximum possible combustion efficiency for rice straws & rice husk is 95.7% at fluidizing velocity of 1.23 m/s in it can be observed that only a slight increase in combustion efficiencies is observed for rice straws & rice husk because of the low ash-fuel ratio. Even though there is a considerable reduction of carbon losses. Permchart and Kouprianov (2004) reported that for the maximum combustor load and with excess air of 50 to 100%, a combustion efficiency of over 99% could be achieved when sawdust and bagasse were fired. In the present study the maximum combustion efficiency is found to be 99.1% for 63% at excess air, which results in higher combustion efficiency at a relatively small quantity of excess air with a minimum heat loss by the exhaust gases.

Even though there is a considerable reduction of carbon losses. Permchart and Kouprianov (2004) reported that for the maximum combustor load and with excess air of 50 to 100%, a combustion efficiency of over 99% could be achieved when sawdust and bagasse were fired. In the present study the maximum combustion efficiency is found to be 99.1% for 63% at excess air, which results in higher combustion efficiency at a relatively small quantity of excess air with a minimum heat loss by the exhaust gases.

The reason for higher combustion efficiency in the present study is due quantity of excess air supplied in the disengagement section.

IV. CONCLUSION

From This Work We Can Conclude That The Minimum Fluidization Velocity Increases With Increase In Fuel Particle Size. Minimum Fluidization Velocity Decreases With Increase In Bed Temperature, Bubble Diameter Increases With Increase In Bed Height And The Mixing Of Solids By (Large) Bubbles Almost Constant Temperature Throughout The Reactor. A Maximum Possible Combustion Efficiency Of 99.1 % Could Be Achieved With The Enlarged Freeboard And The Supply Of Secondary Air In The Freeboard Zone.

Nomenclature

A Cross-sectional area of the bed (m2)

Ar Archrmedes number

dp Feed particle diameter (m)

Db Average equivalent bubble diameter (m)

Dbo Initial bubble diameter (m)

fc Ratio of cloud volume to the volume of bubble

fcw Ratio of volume of cloud-wake phase to the volume of bubble

fw Ratio of wake volume to the volume of bubble

g Acceleration due to gravity (m/s)

H Expanded bed height (m)

Hmf Bed height at minimum fluidization (m)

N Number of equivalent stages

Nor Number of orifice openings in distributor plate

Pav Average pressure in the combustor (atm)

Rg Gas constant (atm-m3/ kg-mole)

Tb Absolute bed temperature (K)

ub Rise velocity of a crowd of bubbles (m/s)

Ubr Rise velocity of an isolated single rising bubble (m/s)

U Superficial velocity (m/s)

Ub Superficial gas velocity of the bubble phase (m/s)

Ucw Superficial gas velocity of cloud-wake phase (m/s)

Umf Superficial velocity of fluidizing gas under minimum fluidization (m/s)

W Fuel feed rate into the combustor (kg/s)

Greek symbols

ρ Density of fluidizing gas (kg/m3)

ρs Density of feed particle (kg/m3)

μ g Viscosity of fluidizing gas (kg/m.s)

ε b Volume fraction of bubbles in the bed

ε mf Voidage at minimum fluidization

ACKNOWLEDGMENT

The authors would like to thank the anonymous reviews of this paper for their fruitful comments and suggestions which greatly improved the quality of this paper.

Tables at a glance

Table 1

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

References

Premchart, W., and Koupranov, V. I., Emission performance and combustion efficiency of a conical fluidized combustor firing various biomass fuels, Bio Resources technology,83-91(2004).
Nag P., Power Plant Engineering, Tata Mcgraw-Hill Publishing Company Limited, New Delhi, (1998).
Domkundwar., and Arora, S., A course in Power Plant Engineering, Dhanpat Rai & Company (P) Ltd., Delhi, (1998).
Wang, A. L., Clough, S. J., and Stubington, J. F., Gas flow regimes in fluidized bed combustor. School of Chemical Engg. and Industrial Chemistry, University of New South Wales, Australia, 29, 819-826, (2002).
Kunni, D., Levenspiel, O., Fluidization Engineering, Wiley, NY, (1969).
Kunni, D. and Levenspiel, O., Bubbling bed model for kinetic processes in fluidized bed, Ind. Engg. Chem. Process Des. Dev., 7, 481-492, (1968).
Davidson, J. F., and Harrison, D., Two Phase Theory of Fluidization, Cambridge University Press, (1963).
Yagi and Kunii D., Studies on combustion of carbon particles in flames and fluidized bed, 5th Int. Symp. On combustion, Reinhold, NY, (1955).