DESIGN CONTROL AND MODELING
OFTHREEPHASEBLDCMOTOR
APPLICATIONSUSINGPID

S.Sathish Kumar; Dr.R.Meenakumari; P.Ravikumar.AP; V.Krishnaveni; K.Kiruthika

DESIGN CONTROL AND MODELING OFTHREEPHASEBLDCMOTOR APPLICATIONSUSINGPID

S.Sathish Kumar¹, Dr.R.Meenakumari², P.Ravikumar.AP¹, V.Krishnaveni³, K.Kiruthika³

Assistant Professor, Dept. of EEE, Jansons Institute of Technology, Coimbatore, Tamilnadu, India
Professor, Dept. of EEE, Kongu Engineering College, Erode, Tamilnadu, India
PG Student, Dept. of EEE, Jansons Institute of Technology, Coimbatore, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The research paper is to develop a complete model of the BLDC motor and to design controller for its position control. PID controllers used for many control problems because of its simple structure, implementation. In practical, we often do not get the optimum performance with the conventionally tuned PID controllers. The efficiency of this method is compared with that of traditional method. I predict results showed that PID control tuned by GA somewhat efficient closed loop response for position control of BLDC motor. The modeling, control and simulation of the BLDC motor have been done using the software.

Keywords

Brushless DC motor, PID control, Pulse Width Modulation.

I. INTRODUCTION

BLDC motors are very popular in does a switch need high performance because of their smaller volume, high force, and simple system structure. In practice, the design of the BLDCM drive involves a complex process such as modeling, control scheme selection, simulation and parameters tuning etc. An expert knowledge of the system is required for tuning the controller parameters of servo system to get the optimal performance. Recently, various modern control solutions are proposed for the optimal control design of BLDC motor [1] [2]. However, these methods are complex in nature and require excessive computation. In contrast, PID control provides a simple and yet effective solution to many control problems [3]. In this paper, extensive mo del ing of a BLDC motor and GA-based PID scheme is proposed for its position control. The paper is organized in the following manner. Section 2 describes mathematical modeling a n d the dr iving c i r c u i t r y o f BLDC motor, section 3 explains the design of PID controller using Ziegler-Nichol’s (ZN) method, section 4 gives brief overview of GA, section 5 briefly illustrate the design of PID controller using GA method, section 6 presents the comparison between the results obtained by the GA and ZN.

II. MATHEMATICALMODELING

The Y-connected, 3-phase motor with 8-pole permanent magnetic rotor is driven by a standard three phase power convertor. The motor specifications are given in Table I.

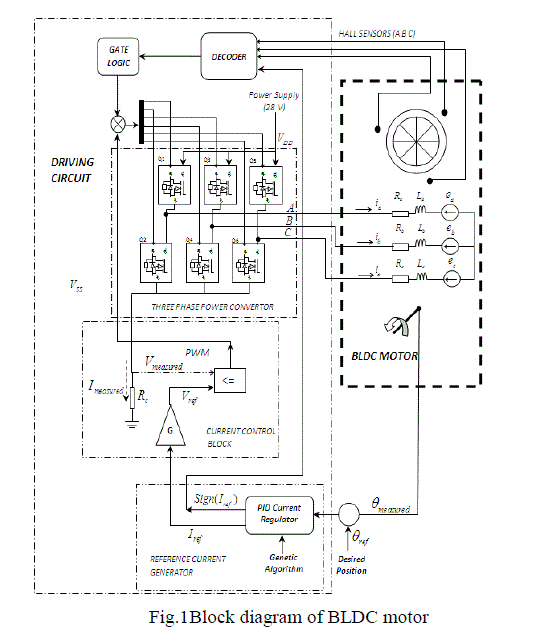
Fig.1shows the basic building blocks of BLDC motor and its Driving circuitry. Driving circuit consists of Reference Current Generator, PID controller, PWM current controller and MOSFET based three phase Power Converter.

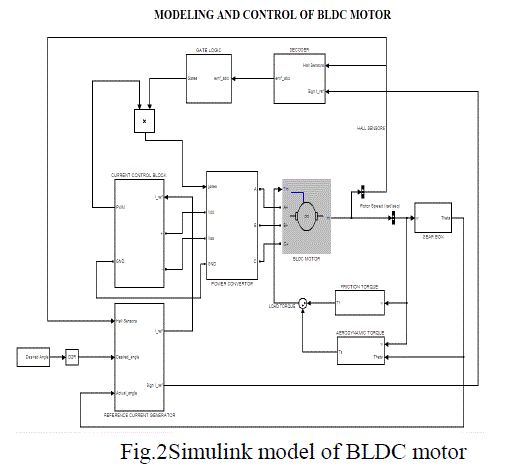
Fig. 2 shows t h e c omp l e t e Simulink model of three phase BLDC motor with its controlling a nd driving circuitry. The detailed descr iption of the major blocks of BLDC motor is mentioned below.

A. ELECTRICALSUBSYSTEM

The electrical part of DC brushless motor and relationship between cur rents , vol tage , and back electromotive f o r c e and rotor velocity is deriving using Kirchhoff’s voltage law [6]:

B. MECHANICAL SUBSYSTEM

A mathematical relationship between the s h a f t a n g u l a r velocity and voltage input to the DC brushless motor is derived using Newton’s law of motion [6].

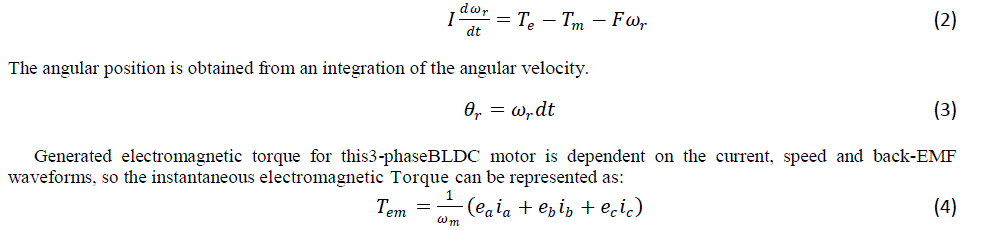C. DESCRIPTION OF DRIVING CIRCUITRY

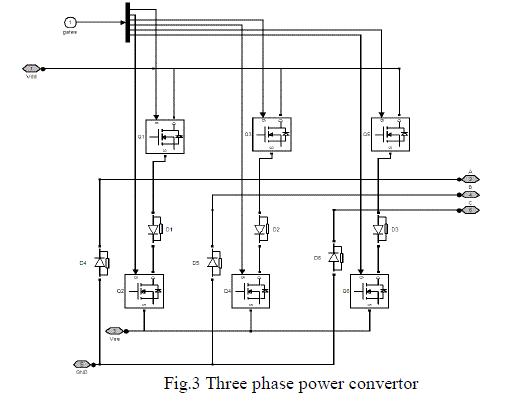
Driving circuitry consist soft three phase power convertors as shown i n Fig.3, which utilize six power transistors to energize two BLDC motor phases concurrently. The r o t o r position, which determines the switching sequence of the MOSFET transistors, is detected by means of 3-Hall sensors mounted on the stator.

By using Hall sensor information and the sign of reference current (produced by Reference c u r r e n t gene r a tor ), De c o d e r block generates signal vector back EMF. The basic idea of running m o t o r i n o p po s i te d i r e c t i o n is by gi vi n g o p p o s i t e current. Based on that, we have Table.4 and Table.5 for calculating back EMF for clockwise and anticlockwise direction of motion as shown below:

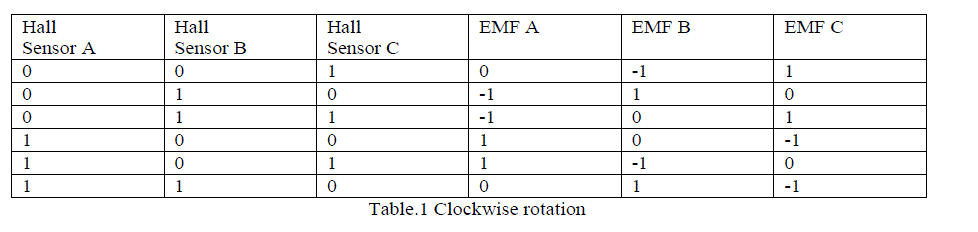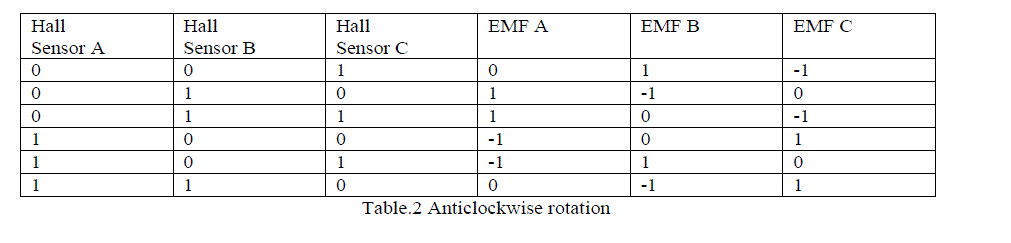In Reference current generator block as shown in Fig.7, PID controller attempts to minimize the difference between desired angle a n d t h e a c t u a l m e a s u r e d angle b y t a k i n g a corrective action to generate reference current signal direction of rotation is based on the sign of that reference current.

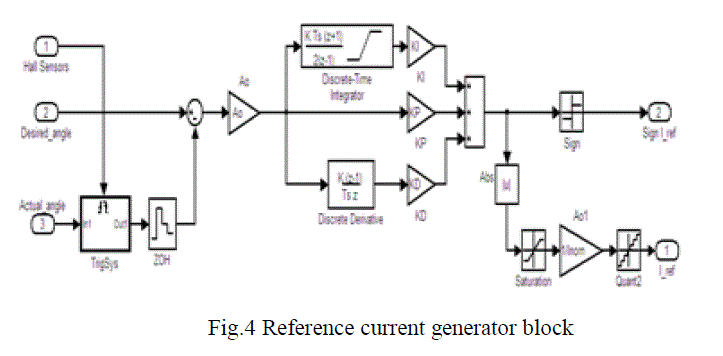In current control block shown in Fig.8, the reference current from current generator is transformed to reference voltage signal by using Ohm’s law (Vref=IrefR).This reference voltage is then compared with the measured voltage across control resistance Rc, where Rc=0.01Ω..When the measured voltage is less than the reference voltage, control signal is set to one for t=2Ts, where Ts is sampling time. In other case control signal is set to zero. In this way a pulse width modulated (PWM) signal having fixed frequency with variable duty cycle is obtained. This PWM signal is then multiplied with the output from gate logic to drive three phase Power Convertor.

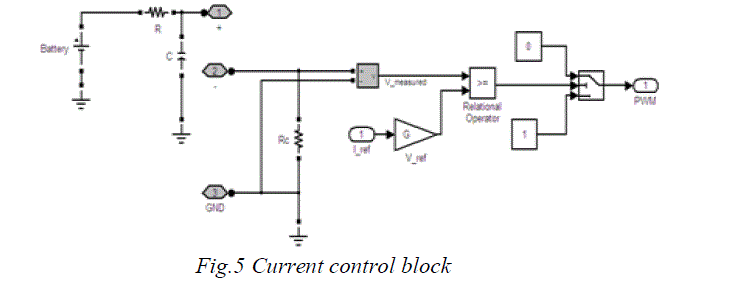III. DESIGN OF PID CONTROLLER USING ZIEGLER-NICHOLS METHOD

The gain tuning of PID is done by increasing the proportional gain until the system oscillates; that gain is Ku.At this instant, time interval is measured between peaks to get Tu. Table V gives approximate values for the controller gains.

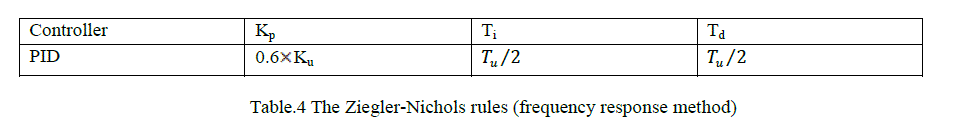From the above algorithm the step response of the system is shown in below Figure:

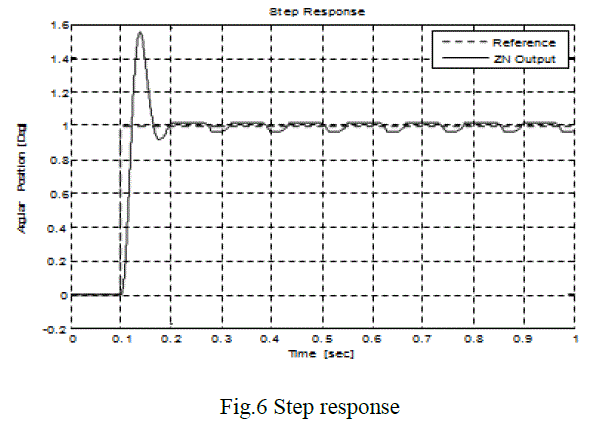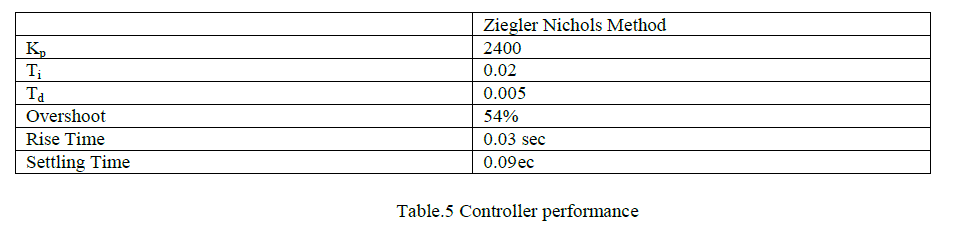
Below analysis d e p i c t s t h a t the s ys t em r e s p o n s e i s not optimum. In order to achieve better performance, GA approach is used to find the optimal value so PID gains.

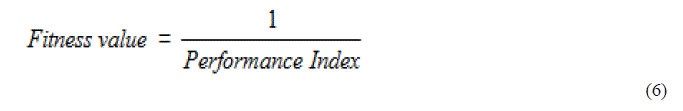D. TERMINATIONCRITERIA

Termination of algorithm takes place when the value of the fitness function for the best point in the current population is less than or equal to fitness limit and the change in the value of fitness function is l e s s t h a n function tolerance. The best member of the population was selected and plotted in the graph. The variation of the PID parameters Kp, Ti and Td are below. It is evident from the results that the best particle has an excellent c o n v e r g e n c e b e f o r e reaching g e n e r a t i o n l imi t . The plot of the error, which is based on IAE criterion for all iterations, is shown in figures below;

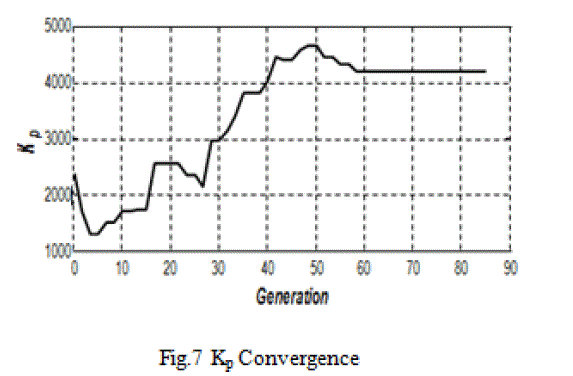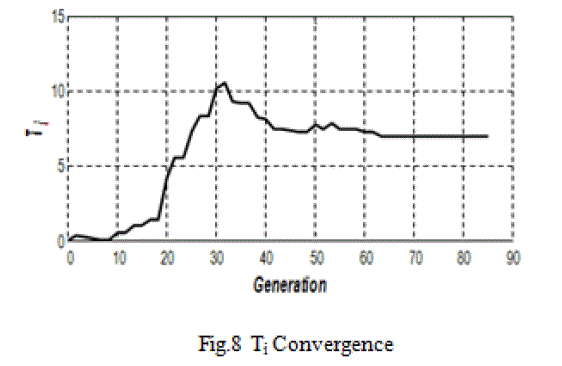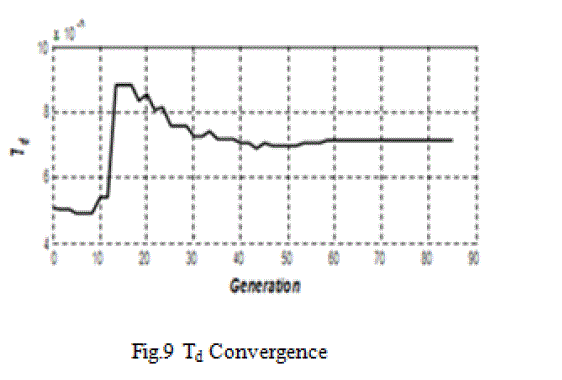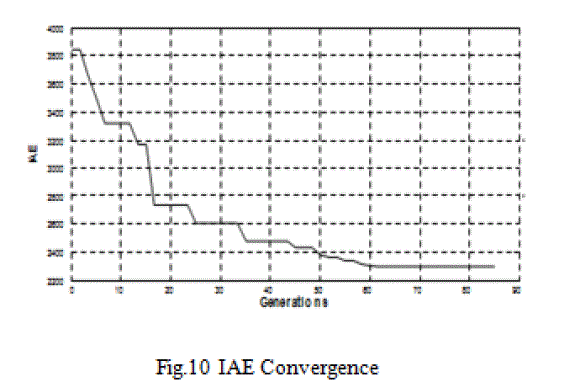PID parameters acquired after GA optimization are listed below:

VI.SIMULATIONRESULTSAND COMPARISON

With optimized PID gains using GA, the step response of the co nt ro l led s y s t e m i s shown i n below along with t h e response obtained from ZN method:

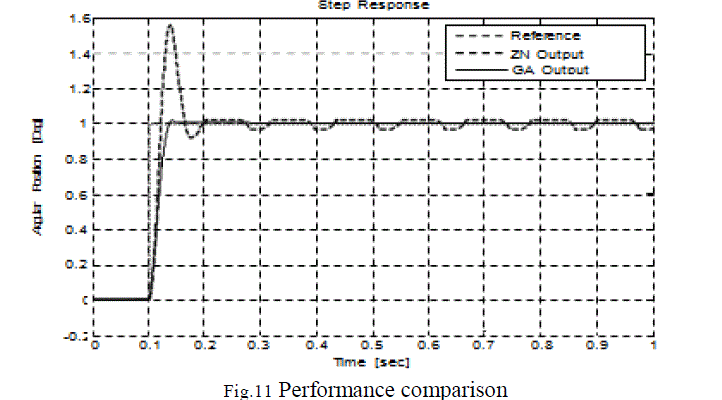It is apparent from the above step response that the controller performance with GA optimized gains is quite efficient as compared to the response obtained from ZN method. The comparison of results in term of rise time, settling time and over shoot are listed in table below:

PERFORMANCE COMPARISON TABLE:

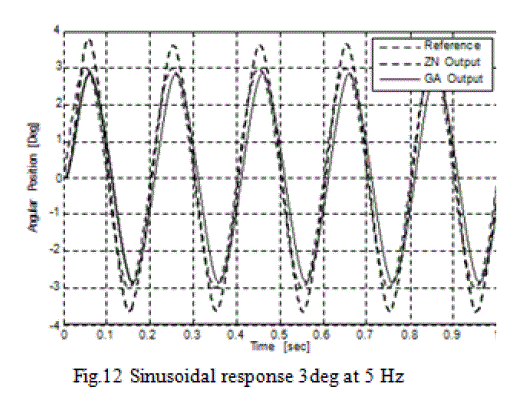
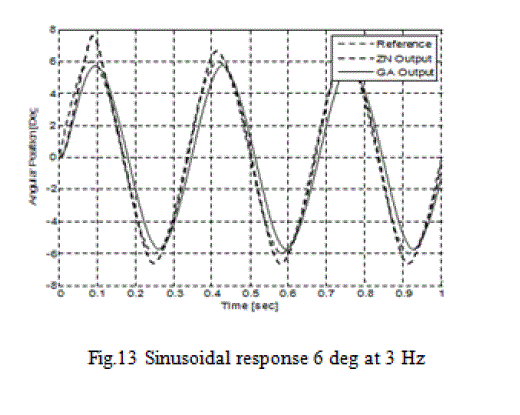
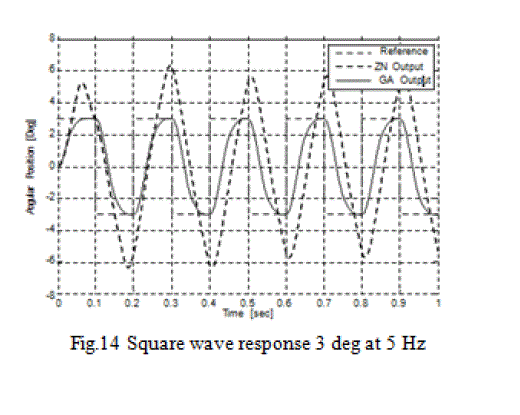
Apart from step response, var ious simulations are carried out in which sinusoidal and square waves having various amplitude and frequencies are applied. Performance comparison of GA optimized controller with the controller tuned by ZN method from various simulations are shown in below Figures:

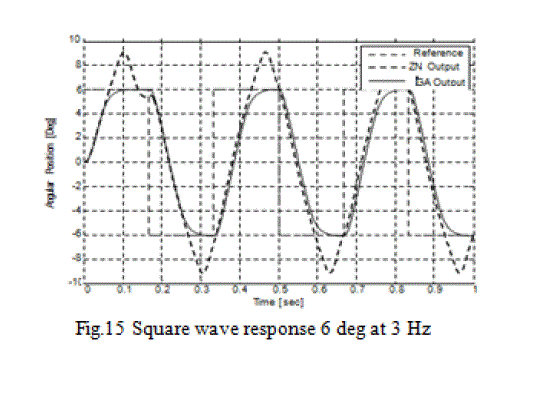It is clear f r om above F i g ures that t h e controller designed with ZN method has high over shoots as was observed in the step response, while the controller with GA optimized gains precisely follows the input signal. Above Figures depict t h a t t h e r e sp o nse o f ZN me t h o d a p p e a r s s i n u s o i d a l against square wave input. There as on is that the controller was still in its transient state when the next pulse is arrived. On the other hand GA based controller achieved its steady state before the next pulse arrived due to its low settling time.

VII. CONCLUSION

In this research paper, modeling of three phase BLDC motor and its optimized PID position control are designed. Comparative study is carried out in which the response of GA based controller is compared with the controller designed using ZN method. It is obvious from review simulation results that the controller performance with GA optimized gains is much more efficient than the ZN method in terms of rise time, settling time, over shoot and set point tracking. However ZN method is good for providing the starting values of PID gains for GA optimization.

References

N.Hemati, J. S. Thorp, and M. C. Leu, “Robust nonlinear control of Brushless dc motors for direct-drive robotic applications,”IEEE Trans. Ind.Electron.,vol.37, pp. 460–468,Dec1990.
P.M.Pelczewski, and U.H.Kunz, “The optimal control of a constrained drive system with brushless dc motor,”IEEE Trans.Ind.Electron., vol.37, pp.342–348, Oct. 1990.
K.Ang, G.Chong, and Y.Li,“PID control system analysis, design, and technology,”IEEE Trans.Control SystemTechnology,vol.13,pp.559- 576,July2005.
T.O.Mahony, CJDowning, and KFatla, “Genetic Algorithm for PID Parameter Optimization: Minimizing Error Criteria”, Process Control and Instrumentation 26-28 July2000, University of Stracthclyde, pg148-153.
David E.Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning. The University of Alabama, Addison-Wesley Publishing Company Inc, 1989.
Atef Saleh Othman Al-Mashakbeh, “Proportional Integral and Derivative Control of Brushless DC Motor”, European Journal of Scientific Research 26-28 July2009, vol.35, pg198-203.