ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| K. Ramesh1, M.Vaidehi2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
A 2-bit Booth encoder with Josephson Transmission Lines (JTLs) and Passive Transmission Lines (PTLs) is designed. The Booth encoding method is one of the algorithms to obtain partial products. With this method, the number of partial products decreases down to the half compared to the AND array method. The circuit area of the multiplier designed with the Booth encoder method is compared to that designed with the AND array method. The proposed 4-bit modified booth encoders are designed using Quartus II. The area, delay and power performance of the booth encoder and modified Booth Encoder have been evaluated from the simulated output analysis shows that modified Booth encoder implemented SFQ multiplier better compared to conventional booth encoder.
Key words |
| Multiplier, booth encoder, (modified booth encoder) MBE, (Single Flux Quantum) SFQ logic. |
INTRODUCTION |
| Low power consumption in CMOS circuits is the present research as high integration causes increases the power dissipation. Single-Flux-Quantum (SFQ) logic circuits attract much attention because of low power dissipation and high throughput. Although the superconductive circuits need a refrigerator system, SFQ circuits have higher advantage compared to semiconductor circuits. The advantages of the SFQ logic are the operation speed and the power dissipation. The AND array method and the Booth encoding method are algorithms for partial product generation. The reduction of partial products is required for higher-bit multiplication, because the addition of partial products stage occupies a large circuit area and causes huge delay |
| In general, a multiplier uses Booth encoder and array of full adders (FAs), or CSA tree instead of the array of FAs. This multiplier mainly consists of the three parts: Booth encoder, a tree to compress the partial products such as CSA tree, and final stage adder. CSA tree is to add the partial products from encoder as parallel as possible. In real implementation, many (4:2) compressors are used to reduce the number of outputs in each pipeline step. The most effective way to increase the speed of a multiplier is to reduce the number of the partial products because multiplication precedes a series of additions for the partial products. To reduce the number of calculation steps for the partial products, Modified Booth Encoder has been applied mostly where CSA tree has taken the role of increasing the speed to add the partial products. |
| The AND array method and the Booth encoding method are algorithms for partial product generation. The reduction of partial products is required for higher-bit multiplication, because the addition of partial products stage occupies a large circuit area. In this paper we present test chips for signed parallel 4-bit multipliers with an AND array or a Booth encoder. |
| In this brief, we present a design technique that improves speed of SFQ multiplier without a power penalty. Based on the proposed technique, the maximum speed of SFQ multiplier can be increased by more than 40% comparing with conventional designs. Moreover, a various multiplier in this table to work almost at the speed SFQ multiplier can be realized. Section II discusses design and analysis. Section III shows simulation and measurement results, followed by the conclusions in Section IV. |
II. ANALYSIS OF MULTIPLIER |
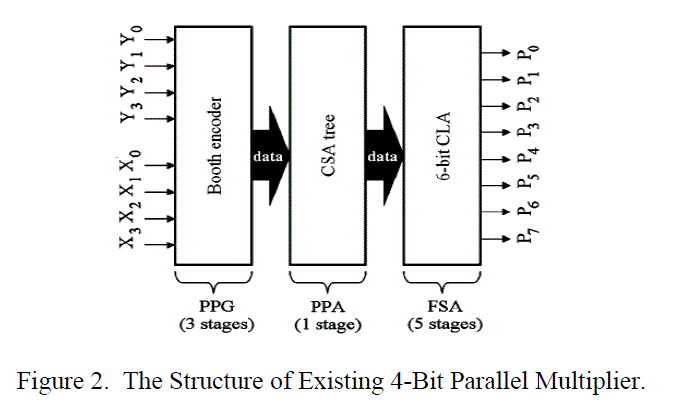
| To realize a high throughput parallel multiplication, We select architecture of general high speed multiplication that divides the multiplier into three blocks; a Partial Product Generator (PPG), a Partial Product Accumulator (PPA), and a Final Stage Adder (FSA) [2], [4]. To execute higher-bit multiplication, we present signed 4-bit multipliers with an AND array or a Booth encoder in PPG block in this paper. |
| A. Partial Product Generator |
| In this section, we explain the algorithm and the structure of the PPG. The AND array method easily generates the logical product of a multiplicand and a multiplier. This method is the simplest architecture for a multiplier. However, this method requires (nxm) many partial products where n and m denote a multiplier and a multiplicand word length, respectively. An AND array is easily designed by using only the AND cells in the cell library. The Booth encoding method is commonly adopted in semiconductor circuits [14]. With his method, we are able to decrease the number of partial products to n/2xm. A Booth encoder has a complicated structure, since an operation of a Booth encoder is complex compared to the AND array method. However, a Booth encoder is able to operate effectively to decrease the number of additions of partial products. The advantage of this method is the reduction of partial products down to the half compared to the AND array method. |
| Assuming that X =(Xn-1 ,Xn-2,….X0) and Y=(Ym-1,Ym-2,….Y0) are a multiplicand and a multiplier, respectively the product Z is Z=X*Y |
 |
| In the Booth encoding method, the multiplier is transformed to |
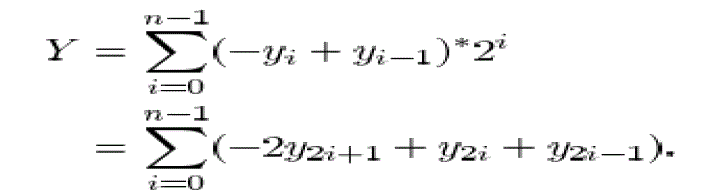 |
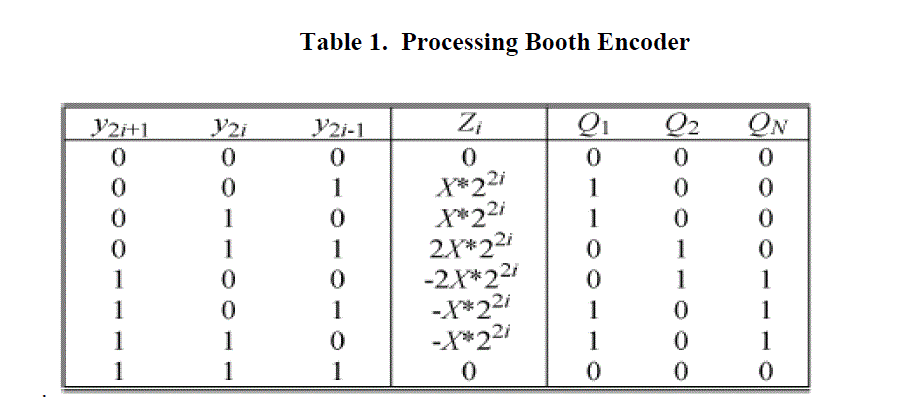
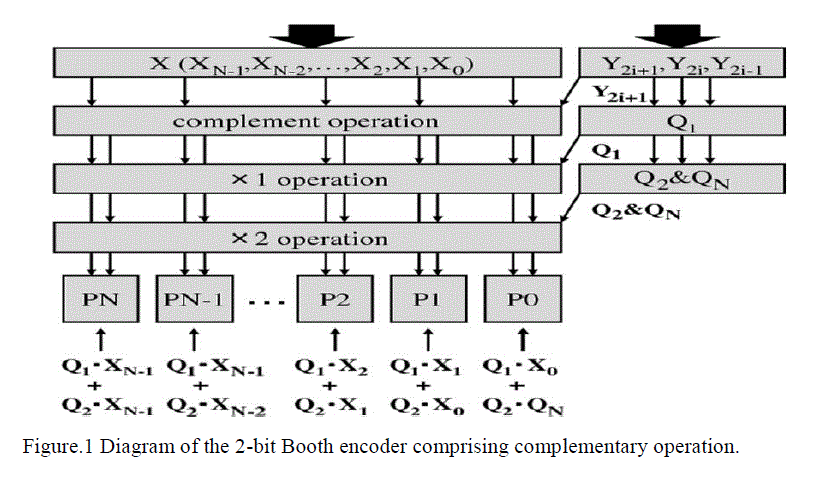
| This method analyses and decodes three bits at each two-bit From Y2i-1 in Table I. Fig. 2 shows a block diagram of 2-bit Booth encoderQ1,Q2 and QN signals are generated as which are easily implemented by SFQ logic circuits. |
 |
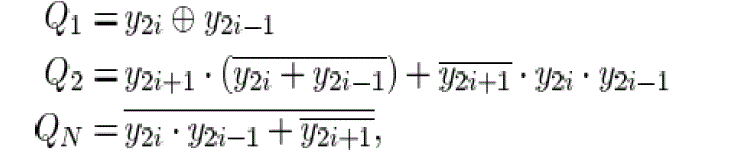 |
| The Booth encoder or the AND array are used for the PPG. Unlike a multiplier using the AND array, the FSA block using the Booth encoder requires a 6-bit Carry Look-ahead Adder (CLA) for 4-bit multipliers. We have designed a 2- bit Booth encoder with Josephson Transmission Lines (JTLs) and Passive Transmission Lines (PTLs). B. Partial Product Accumulator. |
| The PPA block achieves two partial products per bit. We employ a Carry Save Adder (CSA) tree for compression and calculation in the PPA block. The Booth encoder reduces the number of partial products down to the half compared to the AND array method. Table II shows the number of stages in the PPA block under the condition of the given word length of multiplier. The Booth encoding method has less stages from 3 to 5 than those of the AND array method as shown in Table II. These differences have an important meaning in schematic design phase. |
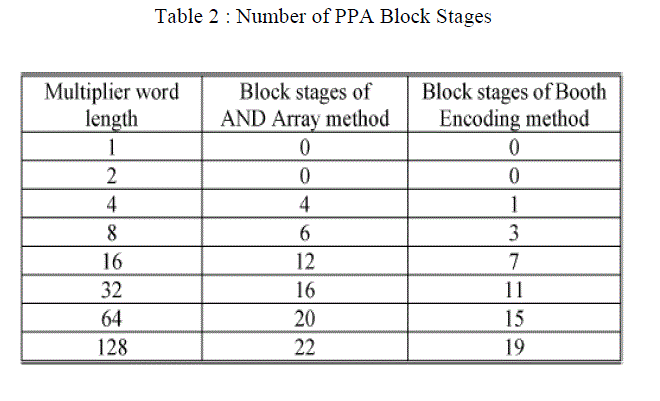 |
| C. Final Stage Adder |
| The FSA calculates a final result from two numbers that are produced by the PPA block. We adopt a CLA and Sklansky algorithm [12] in the FSA block, because they require lower number of Josephson junctions and stages of SFQ logic circuits. Fig.2 shows the structure of the designed 6-bit CLA for the FSA block. |
III. CONVENTIONAL BOOTH ENCODER |
| A 2-bit Booth encoder, a CSA tree and a 6-bit carry look-ahead adder are used for a multiplier operation in the PPG block, the PPA block and FSA block, respectively. Fig.2 shows the diagram of the designed multiplier with the PTLs, and Table III shows its specifications. The multiplier has a 9-stage structure where the PPG block, the PPA block and the FSA block consist of 3 stages, 1 stage and 5 stages respectively. |
IV. PROPOSED WORK |
| A. Modified Booth Encoder (MBE) |
| A modification of the Booth algorithm [10] was proposed by Mac-Sorley in which a triplet of bits is scanned instead of two bits. This technique has the advantage of reducing the number of partial products by one half regardless of the inputs. |
| B. Modified Booth Algorithm |
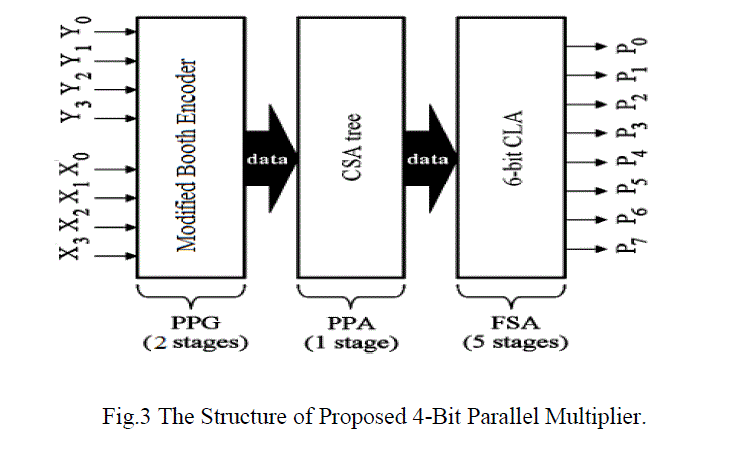
| The multiplier has a 8-stage structure where the PPG block, the PPA block and the FSA block consist of 2 stages, 1 stage and 5 stages respectively. |
 |
IV. PROPOSED WORK |
| A. Modified Booth Encoder (MBE) |
| A modification of the Booth algorithm [10] was proposed by Mac-Sorley in which a triplet of bits is scanned instead of two bits. This technique has the advantage of reducing the number of partial products by one half regardless of the inputs. |
| B. Modified Booth Algorithm |
| The multiplier has a 8-stage structure where the PPG block, the PPA block and the FSA block consist of 2 stages, 1 stage and 5 stages respectively. |
 |
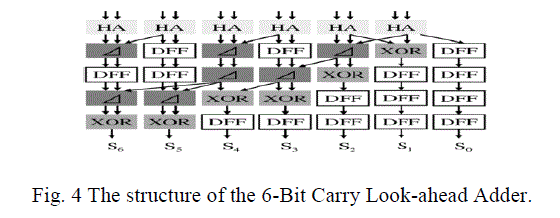 |
| When the number of partial products is reduced to sum and carry words, a final adder is required to generate the multiplication result. The number of bits of the final adder is the sum of the number of bits of the multiplier and multiplicand. Thus, the data path width is usually doubled and the delay of this stage is most severe. Normally 6-bit CLAs [4] can be used to reduce the delay and area requirements. This adder is a practical design with reduced delay at the price of more complex hardware. |
V. SIMULATION RESULTS |
A. Partial Product Generation: |
| The Quartus II tool is used to obtain the simulated output for booth and modified booth encoder. The simulated waveforms are obtained by assigning the input values at various levels of extraction and the corresponding outputs are obtained from the assigned inputs. The outputs obtained are complementary with respect to the corresponding complementary inputs. The simulated waveforms of the proposed work are shown here. Figure 5 shows the simulated output of modified Booth encoder. Output are realized based on the logic design of the encoder which is verified. |
 |
B. Simulated Waveform of Modified Booth Encoder |
 |
| Figure 6 illustrates the output waveform of Modified Booth Encoder. Here the 4- bit multiplier and multiplicand are given as inputs and 8- bit final product is the generated output. |
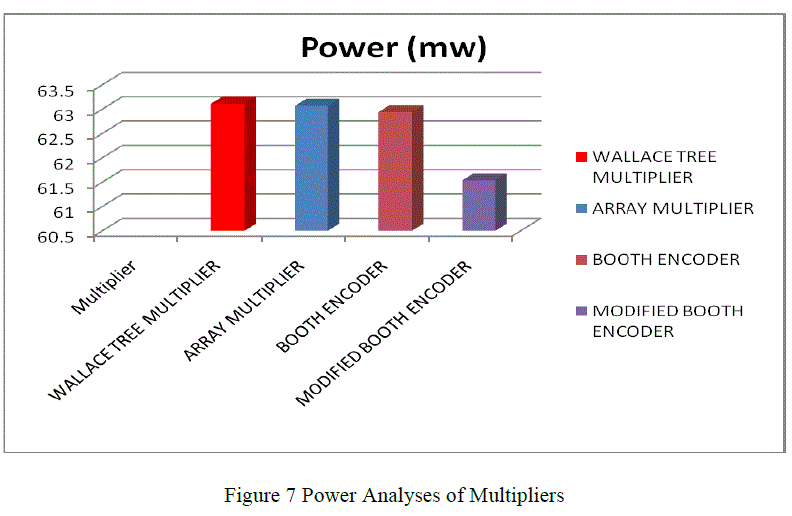 |
| The power dissipation of modified booth encoder SFQ multiplier demonstrates an power reduction of 22.24 % compared to booth encoder based SFQ multiplier. This reduction in power is due to the reduced number of partial product generation units in modified booth encoder based SFQ multiplier. Also the power of modified booth encoder based SFQ multiplier demonstrates better power saving compared to array and Wallace tree multiplier |
D. Delay Analysis |
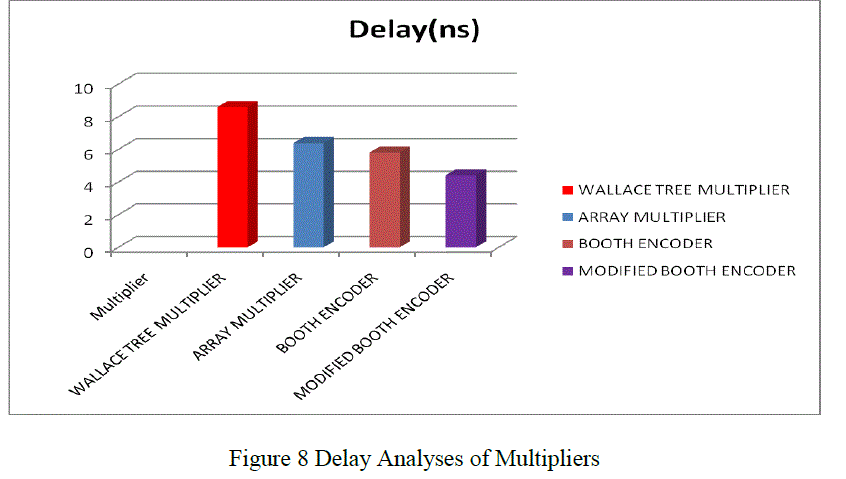 |
| The delay of modified booth encoder SFQ multiplier demonstrates a delay reduction of 23.96 % compared to booth encoder based SFQ multiplier. This reduction in delay is due to the reduced number of partial product generation units in modified booth encoder based SFQ multiplier. Also the delay of modified booth encoder based SFQ multiplier demonstrates better delay saving compared to array and Wallace tree multiplier. |
E. Logic Cell Analysis |
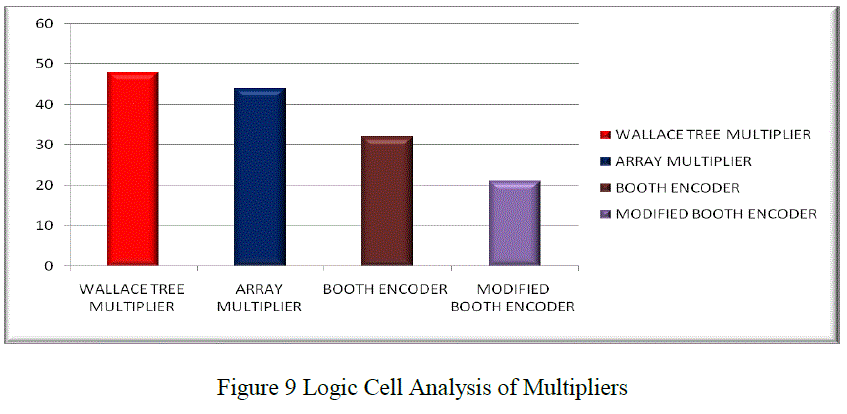 |
| The logic cell count of modified booth encoder SFQ multiplier demonstrates an area reduction of 34.37 % compared to booth encoder based SFQ multiplier. This reduction in logic cell count is due to the reduced number of partial product generation units in modified booth encoder based SFQ multiplier. Also the logic cell count of modified booth encoder based SFQ multiplier demonstrates better area saving compared to array and Wallace tree multiplier. |
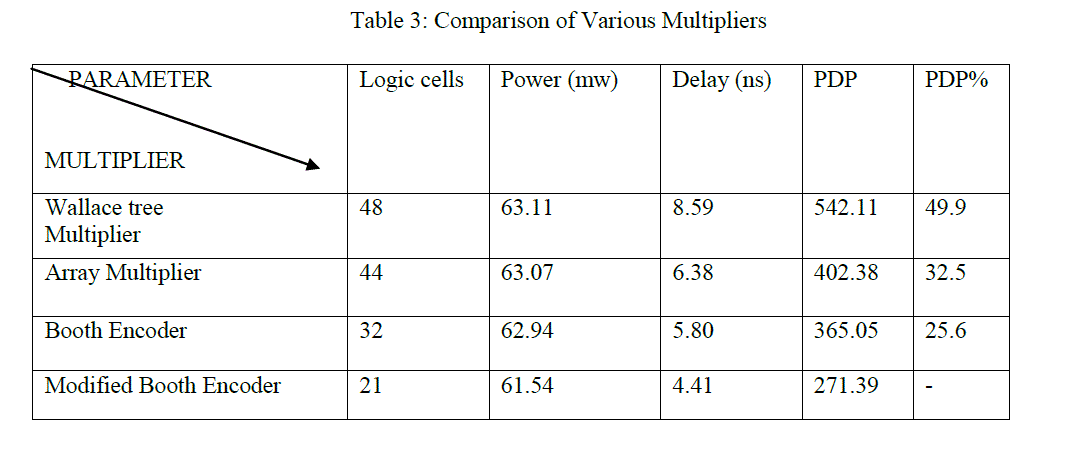
| Table illustrates power, delay and power delay product parameters of booth encoder and modified booth encoder. Table IV shows that power consumption is reduced compared to conventional booth encoder. Similarly in modified booth encoder delay is very less which results high speed operation due to the presence of modified booth encoder. |
 |
VI. CONCLUSION |
| Multipliers are one of the most important components of DSP systems. Critical delay of the DSP architecture depends on the computation time of the multiplier unit. This Method is used to reduce computation time of a multiplier unit not only increase the speed of DSP architecture but also reduce the power consumption. Booth encoder came as a best choice for critical delay applications. In the existing Booth encoder, based on Radix-2 algorithms by which number of partial products are more. In the proposed modified booth encoder based on radix-4 algorithms by reducing number of partial product. Results shows that proposed modified booth algorithm consumes 25%. Thus modified Booth encoder is considered as best choice for power critical applications. |
References |
|