Research & Reviews: Journal of Material Sciences
MenuISSN:2321-6212
ISSN:2321-6212
James N Monks1,2*, Andrew Hurst2, Zengbo Wang1
1 Department of Computer Science and Electronic Engineering, Bangor University, Gwynedd, United Kingdom
2 Qioptiq Ltd, Denbighshire, United Kingdom
Received: 12-Aug-2022, Manuscript No. JOMS-22-71820; Editor assigned: 16-Aug-2022, PreQC No. JOMS-22-71820(PQ); Reviewed: 30-Aug-2022, QC No. JOMS-22-71820; Revised: 6-Sep-2022, Manuscript No. JOMS-22-71820(R); Published: 13-Sep-2022, DOI: 10.4172/2321-6212.10.7.003.
Visit for more related articles at Research & Reviews: Journal of Material Sciences
Thin film technology has played an important role for optical filters with many complex designs and configurations used, such as Bragg, Dichroic and Rugate. In recent years, metamaterials have aimed to simplify the configuration and improve performance by applying the complexity to the material itself. In this research, we put forward a design technique that integrates visible wavelength plasmonic resonators with nano pyramid structured anti-reflection coatings to produce high performance fixed-line notch filters at visible wavelengths. The pyramid structure notch filters can provide a high transmission band surrounding the rejected wavelengths by mimicking gradient index transitions, whilst remain shift-free for oblique incidence angles, unlike the thin film counterparts. As an example, this research also demonstrates a 532 nm notch filter specifically designed for laser glare and dazzle protection.
Optical filters; Nanostructures; Plasmonics; Metamaterials
In 1817 Joseph von Fraunhofer discovered the Anti-Reflection (AR) effects of a single layer on glass [1]. Although Fraunhofer himself never followed up on this particular development, his observations did lay the foundations in this field. The development for modern thin film optical coatings amplified in the 1930s with the independent works of Rouard [2], Bauer [3], Pfund [4], Strong [5], Smakula [6], and Geffcken [7]. The extension of AR films to optical filters was underpinned by Lawrence Bragg and his father, William Henry Bragg [8]. The father and son duo defined Bragg’s law for X-ray crystallography, and in doing so, they also provide a description for the effects of constructive and destructive interference, the governing principle for optical filters. The technological advancements in optical coatings significantly improved the performance due to the sudden expansion of optical systems, particularly photographic objectives that demanded more complex antireflection coatings. World war-II witnessed a huge development that saw coatings as a necessity for optical systems. With today’s optical systems, it is almost impossible to imagine an optical device that would not rely on an optical coating to assure and improve functionality and performance. It is not uncommon for modern optical filters to have greater than 100 layers, and the uses have been unearthed for them in virtually all branches of science and technology.
The underlying technology for optical filters has, although significantly improved, remained the same and consists of transparent thin film layers with alternating and contrasting refractive indices. The layer thicknesses are designed to produce destructive and constructive interference in the reflected and transmitted beams [9], depending on the application and type of filter. Consequently, due to nature of this design, the layer’s performance change with incident angle due to a change in phase thickness. Thus, making optical filters extremely angular sensitive [10]. Metamaterials have been highlighted as a strong contender to improve the angular performance of optical filters [11,12] without the emission of fluorescence found in conventional dye molecules.
The exploration of artificial material for the intended purpose of electromagnetic wave manipulation began towards the later end of the 19th century [13] and have grown with interest as the technology begins to mature away from fundamental research. Unlike traditional materials where the chemical structure influences the electromagnetic properties, metamaterials do so from their physical structures. To affect electromagnetic radiation, the metamaterials atoms, known as meta-atoms or unit-cells, represent physical features much smaller than the wavelength to behave as a homogeneous material when arranged in some form of Bravais lattice. As such, at optical frequencies, the structures must remain on the nanometer scale [14].
Researchers have demonstrated applications and designs for the use of metamaterials as optical filters, but the outputs often lack the performances that thin films demonstrate at normal incidence [11,12,15]. One such example can be found with moth eye nanostructures, which exceed thin film anti-reflective performance [16]. In nature, moth’s eye has an unusual property where the surface of their eyes is covered with natural nanostructures as a form of camouflage [17]. Researchers have taken this idea and demonstrated antireflection coatings with surface structures that act as gradient index features [18]. A simplified moth eye design can be constructed using nano pyramids to achieve the same antireflection properties found in moth eyes [19]. Furthermore, our previous research demonstrated how plasmonic metamaterials could be used for laser protection eyewear but ultimately lacked ‘near-perfect’ out-of-resonance transmission [12]. The research presented in this article merges pyramid structure structures with plasmonic nanoparticles to significantly improve the optical performance of a fixed-line metamaterial notch filter. The plasmonic nanoparticles acts as packets of electrical charge that collectively oscillate at the surface when subjected to a particular wavelength, resulting in improved light blocking at that precise wavelength.
Analytical theories including Mie theory and thin film interference theory, has provided the base design principles for this research. Subsequently, the use of a full-wave numerical simulation software (CST Microwave Studios) has been used to solve the far field responses. The optical properties for the materials refractive indices and extinction coefficients have been obtained from literature. The light propagation direction, K-vector, with normal incidence is perpendicular to the design surface. For incidence angle (theta) studies, the propagation direction has varied from the normal incidence plane. The electric field is directional to the y-axis and the magnetic field is directional to the x-axis. The generalised design approach has swept the pyramid structure refractive index from a range of 1.38 to 3.
Physics and design protocol
Tuning of notch filter wavelength by plasmonics: A plasmon arises from a collective oscillation of free electrons in a noble metal, analogous to a mechanical oscillation of the electron gas of a metal [20]. With the presence of an external electric field, the electron gas becomes displaced with respect to the fixed ionic cores. At the surface of a noble metal, such as gold and silver, the plasmon takes the form of Surface Plasmon Polaritons (SPPs). These surface plasmons are optically excited and upon incidence, light can be coupled into a standing or propagating surface plasmon mode. When a surface plasmon is confined to a nanoparticle, the particle’s free electrons contribute to the collective oscillations that are localised to the nanoparticle itself. This is known as a Localised Surface Plasmon (LSP) [21]. There are two major implications of the LSP. First, electric fields at the particle’s surface are considerably amplified, with the enhancement being greatest near the particle’s surface and rapidly diminishing as the distance increases. Secondly, the particle’s optical extinction peaks at the plasmon resonance frequency, which for noble metal nanoparticles occurs at the visible wavelengths. This extinction peak depends on the refractive index of the surrounding medium and is the basis for fixed- line optical metamaterial notch filters. Scattering theory (Mie theory, Gans theory) provides a deep understanding of how Localised Surface Plasmon Resonance (LSPR) arises.
In Figure 1a, the real component of the complex dielectric functions of bulk silver and gold [22] are plotted, as experimentally determined by Johnson and Christy. The dependence of the LSPR peak on the surrounding dielectric environment, Figure 1b, is a condition met when−2εd, where εd is the real permittivity of the surrounding dielectric environment. For example, for gold nanoparticles in water (εd=1.33), the expected resonant wavelength is about 501 nm. The sensitivity εd is derived from the slope of the real component of the dielectric function in the observed wavelength range. The LSPR wavelength for silver will be bluer (shorter wavelength) than that of gold for a given external dielectric constant. In the plasmon resonance, the imaginary part of the dielectric function plays a role in the dampening or broadening of the resonance peak. As shown in Figure 1b, by using gold and silver nanoparticles within various surrounding refractive index environments, the LSPR can span the entire length of the visible spectrum.
Figure 1: (a) The permittivity (real part) for silver and gold according to Johnson and Christy. (b) The localised surface plasmon resonance wavelength for silver and gold nanoparticles with varying refractive index for the surrounding material and a fixed particle size of 20 nm. ?
Enhancing transmission with pyramid structure anti-reflection structure: Figure 2 presented the effectiveness for the transmission of a pyramid structure design as an antireflection coating when compared to a thin film layer at quarter-wave thickness, with varying refractive indices.
Figure 2: Transmission contour plots as function of refractive index of top film layer and incident wavelength for (a) Thin film on glass substrate with varying refractive index for the layer interfacing with air, and (b) for a pyramid structure design with varying refractive index.
The pyramid structure example here does not have any plasmonic resonators to solely demonstrate the high transmission advantages. The standard thin film design (Figures 2a and 2b) consisted of the following layer configuration with λ0=550 nm
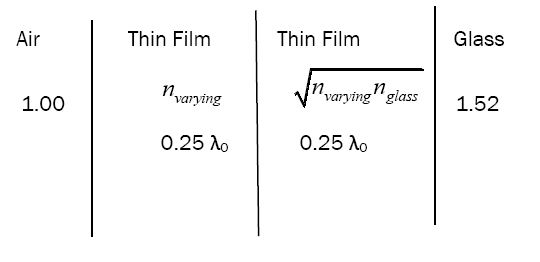
The performance of the thin film configuration, with the top thin film layer at indices below 1.52, provides some anti-reflection properties. However, for indices above the 1.52 threshold, the transmission begins to greatly reduce with the reflections reaching around 40% when nvarying=3. Unlike the thin film counterpart that displays a dramatic change in the refractive index at the interfaces, the pyramid structure has a continuous refractive index gradient between air and the medium that decreases reflections by effectively removing the air-to-thin film interface. A notable mention for the pyramid structure is that at the lower index range, the antireflection properties provide a broadband solution. However, as the index of the pyramid structure increase, the antireflection properties become less broadband and with the peak transmission remaining at the reference wavelength at around 99.98%. The reflection at the furthest wavelength from the reference wavelength never drops below 4%. The design configuration for the pyramid structure can be found in Figure 3 without the presence of the plasmonic nanoparticles.
Figure 3: The side-on design for the fixed-line optical notch filter. Insert shows the 3D structure with the simulation mesh.
The quarter-wave design principles for standard optical thin films provides the basis for the pyramid structure dimensions. The noticeable difference is that the pyramid structure itself must be of considerable height for an efficient gradient to occur. If the height is not at a sufficient gradient, then the incoming wave will experience a phase change at the interface due to an impedance mismatch, resulting in unwanted reflections. To increase the gradient and reduce the reflected light, the pyramid structure thickness, h, must have an odd-integer multiplication factor, m, so any reflected light destructively interferes with the incoming light to produce a phase difference of mπ
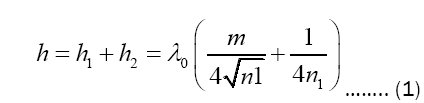
To prevent a sharp change of index and preclude further unwanted reflections between the pyramid structure and glass substrate, a simple thin film matching layer has been included with a refractive index of n2.
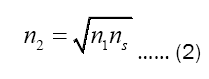
As the matching layer is a traditional, non-structured coating, the thickness of the coating can be calculated at a quarter wavelength.
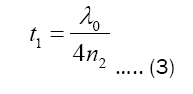
The side-on configuration of the pyramid structure metamaterial notch filter can be found in Figure 3, with the insert showing the actual three-dimensional simulated structure. The pyramid structures act as the pyramid structure features and provides a gradient index to produce high transmission. The refractive index of the pyramid structure and the plasmonic resonator material is determined by the desired notch wavelength, as described by the localised surface plasmon resonance, Figure 1b. The matching layer can be determined from the chosen pyramid structure index. For example, if a desired notch filter at 550 nm is required, in accordance with the LSPR, a silver nanoparticle can be selected and surrounded by a pyramid structure structure with a refractive index of 2.46. The matching layer between the glass substrate and pyramid structure would be then 1.93, according to Equation 2.
The design found in Figure 3 enables an easy design route for a fixed-line optical notch filter by simply selecting the material properties according to the LSPR. At the resonant wavelength, the absorption and scattering functions increase and result in a significant drop in transmission. The effects on adjusting the pyramid structure material’s refractive index for the transmission spectrum can be found in Figure 4. The contour transmission plots demonstrate that silver remains the ideal material choice because unlike gold, the transmission attenuation does not alter across the refractive index range. The gold counterpart does not provide strong LSPR with low refractive index environments but allows a notch selection at the longer visible wavelength range beyond what silver can offer.
Figure 4: Contour plot of transmission as function of laser wavelength and pyramid structure refractive index for (a) silver and (b) gold-based filter.
Traditional thin film notch filters are designed with quarter-wave thick layers of alternating refractive indices to create destructive and constructive interference to filter out the unwanted wavelengths. It is not uncommon for these designs to have up to 100 layers. The layer number governs the steepness of the transition from high transmission to low transmission. The designs themselves must also be complex to remove the pronounced ripples in the passband region that are produced due to the mismatching of the equivalent optical admittance of the substrate, multilayer stack, and air. Due to the thin film filters design, they are extremely angular sensitive. The disparity of performance with incidence angles is a well-known effect and has been widely studies [11].
As the angle of incidence increase from the normal incidence of the thin film filter, the transmission notch shifts towards the blue spectrum, and away from the desired blocking wavelength. As the filters notch shifts, it also begins to split the S-(TE) and P-(TM) polarisations.
The design process presented in this study, mitigates most the problems presented by the traditional thin film filters. The metamaterial notch filter does not present ripples in the passband because of the gradient transition between air and the pyramid structure. Furthermore, the proposed filter is not angular sensitive or polarisation sensitive because the plasmonic resonators are able to create a strong electric resonance at the blocking wavelength which can create circulating currents to efficiently drive a magnetic response. The strong electric and magnetic responses lead to angular stability because of the symmetry and equivalent inductance of the meta-atom. To demonstrate this, an example narrowband notch filter has been designed using the techniques described in this research.
Application demonstration: 532 nm narrowband filter
The 532 nm filter is a common wavelength of choice for notch filters and has numerous applications in laser science and laser dazzle protection, where the optical density does not need to completely attenuate the laser but merely protect again dazzling effects. Here, the new pyramid-plasmonic composite metamaterial design is presented.
The configuration for the metamaterial narrowband notch filter is set out in Figure 3. This design demonstrates the excellent performance of a metamaterial filter, as presented in Figure 5. The LSPR for silver nanoparticles with a diameter of 20 nm at the wavelength of 532 nm is ~2.36. The material availability with a refractive index closely matched to this is Zinc Sulphide (ZnS). As such, the matching layer can be determined and the closest material to support the given refractive index is Hafnium dioxide (HfO2).
Figure 5: Pyramid-plasmonic composite metamaterial filter design showing shift-free angular performance. A. Fixed line transmission at θ=0°, θ=30° and θ=60°. B. The parametric mean transmission plot for angular studies. C. The optical density vs. incidence angle. D. The CIE 1931 colour map demonstrating the colouration for the given filter. E. The IVT vs. incidence angle. 
The metamaterial design displays no blue shift with increased incidence angles and has no ripples in the passband regions with near 100% transmission. The Integrated Visual Transmission (IVT) is the function associated with the average spectral sensitivity of the filter in accordance with the typical human visual perception and is important to understand how the human eye will interact visually with the filter. The average IVT for the presented filter is ~77%. The Optical Density (OD) defines the degree to which a medium impedes transmitted light waves and is a common measure for optical filters. The OD remains around 1 and increases with high angles of incidence. All optical filters will experience a degree of functional visual impairment which also relates to the filter colouration. The standard analysis for colouration is the CIE 1931 colour map. Due to individual variation of the human eye, the distribution of cones in the eye result in the tristimulus values being dependent on the observer’s field of view. The CIE 1931 colour map represents a chromatic response for the average human within a 2° arc inside the fovea centralis, a region of closely packed cones in the eye; thus, providing the user confidence of the correct colouration response. The colouration presents a magenta hue in the transmission mode and a Munsell green hue in the reflection mode.
Manufacturing
The pyramid structure metamaterial notch filter retains similar levels of manufacturing difficulty as the previously published design [12]. However, the pyramid structure design displays larger plasmonic nanoparticles than the sub-10 nm design previously reported [12]. Nanoscale self-assembling materials suc24h as Block-Copolymers (BCPs) can achieve discrete ordered morphologies over a large area with a continuously uniform natural period with a high-order natural spacing length ranging from 10 nm to 200 nm [23]. This self-assembled arrangement can organise the plasmonic nanoparticles into a periodic array, with multilayer fabrication stacking forming a three-dimensional assembly process [24]. Furthermore, research has demonstrated that the BCPs can also create reactive ion etching masks for pyramid structure antireflection coatings [25]. As such, BCPs could simplify the manufacturing process by acting as a temporary film for particle placement and a RIE mask for developing pyramid structures.
As the functionality requirements for optical systems increase with technological demand, so does the challenge for improved performance of optical thin film filters. Metamaterials have been a highlighted route for meeting this demand of enhanced output. One such filter that is in high demand is the optical notch filter. Our research presents a new route to design a metamaterial notch filter that merges pyramid structures and plasmonic resonators. The approach enables a reference blocking wavelength to be selected according to the localised surface plasmon resonance of a metallic nanoparticle. This nanoparticle is embedded within a pyramid structure. The function of the pyramid structure allows for near-perfect transmission in the passband regions, whilst the resonator provides wide-angle blocking at the reference wavelength. This research presents a promising route for novel design high performance optical metamaterial filters that could be used in a wide variety of applications.
Part-funded by the European Regional Development Fund through the Welsh Government.
[Crossref] [Google scholar][EBSCO]
[Crossref][Google scholar] [EBSCO]
[Crossref] [Google scholar][EBSCO]
[Google scholar] [EBSCO]
[Crossref] [Google scholar][EBSCO]
[Crossref] [Google scholar][EBSCO]
[Crossref] [Google scholar][EBSCO]