Detecting and Correcting Multiple Cell Upsets
With 64-Bit Decimal Matrix Code in Memories

N.V.Satyanarayana; Ch.N.L.Sujatha; J.S.S.Ramaraju

Detecting and Correcting Multiple Cell Upsets With 64-Bit Decimal Matrix Code in Memories

N.V.Satyanarayana1, Ch.N.L.Sujatha2, J.S.S.Ramaraju3

M.Tech ECE Pursuing, Bhimavaram Institute of Engineering & Technology, West Godavari, A.P, India
Assistant Professor, Department of ECE, Bhimavaram Institute of Engineering & Technology, West Godavari, A.P, India
Assistant Professor, Department of ECE, Bhimavaram Institute of Engineering & Technology(BVRM), West Godavari,
A.P, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The proposed security code utilizes decimal method to detect errors, so that more errors were detected and corrected. At the present days to maintain good level of reliability, it is required to protect memory cells using protection codes, for this purpose, various error detection and correction methods are being used. In the paper 64-bit Decimal Matrix Code was proposed to assure the dependability of memory. Here to detect and correct up to 50% errors. The results showed that the proposed scheme has a protection level against large MCUs in memory. To avoid MCUs from causing data corruption, more complex error correction codes (ECCs) are widely used to protect memory, but the main problem is that they would need higher delay overhead. Previously, matrix codes (MCs) based on Hamming codes include been proposed for memory safety. The main problem is that they are double error correction codes and the error correction capabilities are not enhanced in each case. Transient multiple cell upsets (MCUs) are appropriate major problems in the reliability of memories exposed to energy environment. In the new method we are implement 64-bit decimal matrix for error correction in memories. In the new method to increase the error correction rate compared to the 32-bit decimal matrix code. Moreover, the ERT (encoder-reuse technique) is proposed to decrease the area transparency of extra circuits exclusive of disturbing the total encoding and decoding processes. ERT (encoder re use technique) use DMC encoder itself to be part of in the decoder.

Keywords

Error correction codes (ECCs), mean time to failure (MTTF), memory, Hamming code, multiple cells upsets (MCUs), memory.

INTRODUCTION

The general idea for achieving error detection and correction is to add some redundancy (i.e., some extra data) to a message, which receiver can use to check consistency of the delivered message, and to pick up data determined to be corrupt. Error-detection and correction scheme can be either systematic or non-systematic: In a systematic scheme, the transmitter sends the unique data, and attaches a fixed number of check bits (or parity data), which are derived from the data bits by some deterministic algorithm. If only the error detection is required, a receiver can simple apply the same algorithm to the received data bits and compare its output with the receive check bits; if the values do not match, an error has occurred at some point throughout the transmission. Error-correcting codes are regularly used in lower-layer communication, as well as for reliable storage in media such as CDs, DVDs, hard disks and RAM.

In a system to uses a non-systematic code, the unique message is transformed into an encoded message that has at least as many bits as the unique message. The aim of error detection and correction code is to provide against soft errors that manifest themselves as bit-flips in memory. Several techniques are used present to midi gate upsets in memories. For example, the Bose–Chaudhuri–Hocquenghem codes [8], Reed–Solomon codes [9], punctured difference set (PDS) codes [10], and matrix codes has been used to contact with MCUs in memories. But the codes require more area, power, and delay overheads since the encoding and decoding circuits are more complex in these complicated codes. Reed-Muller code [14] is another protection code that is able to detect and correct additional error than a Hamming code. The main drawback of this protection code is its more area and power penalties

Hamming Codes are more used to correct Single Error Upsets (SEU’s) in memory due to their ability to correct single errors through reduced area and performance overhead [13]. Though brilliant for correction of single errors in a data word, they cannot correct double bit errors caused by single event upset. An extension of the basic SEC-DED Hamming Code has been proposed to form a special class of codes known as Hsiao Codes to increase the speed, cost and reliability of the decoding logic [14].

One more class of SEC-DED codes known as Single-error-correcting, Double-error-detecting Single-byte-error-detecting SEC-DED-SBD codes be proposed to detect any number of errors disturbing a single byte. These codes are additional suitable than the conventional SEC-DED codes for protecting the byte-organized memories [15][16]. Though they operate through lesser overhead and are good for multiple error detection, they cannot correct multiple errors. There are additional codes such as the single-byte-error-correcting, double-byte-error-detecting (SBC-DBD) codes, double-error-correcting, triple error-detecting (DEC-TED) codes that can correct multiple errors as discussed in [10].

The Single-error-correcting, Double-error-detecting and Double-adjacent-error-correcting (SEC-DED-DAEC) code provides a low cost ECC methodology to correct adjacent errors as proposed in [12]. The only drawback through this code is the possibility of miss-correction for a small subset of many errors.

AS CMOS technology scales down to nano-scale and memories are combined through an increasing number of electronic systems, the soft error rate in memory cells is rapidly increase, especially when memories operate in space environments due to ionizing effects of atmospheric neutron, alpha-particle, and cosmic rays.

Interleaving technique has been used to restrain MCUs, which rearrange cells in the physical arrangement to separate the bits in the same logical word into different physical words. However, interleaving technique may not be practically used in content-addressable memory (CAM), because of the tight coupling of hardware structures from both cells and comparison circuit structures.

Built-in current sensors (BICS) are proposed to assist with single-error correction and double-error detection codes to provide protection against MCUs. However, this technique can only correct two errors in a word.

More recently, in 2-D matrix codes (MCs) are proposed to efficiently correct MCUs per word with a low decoding delay, in which one word is divided into multiple rows and multiple columns in logical. The bits per row are protected by Hamming code, while parity code is added in each column. For the MC based on Hamming, when two errors are detected by Hamming, the vertical syndrome bits are activated so that these two errors can be corrected. As a result, MC is capable of correcting only two errors in all cases. In an approach that combines decimal algorithm with Hamming code has been conceived to be applied at software level. It uses addition of integer values to detect and correct soft errors. The results obtained have shown that this approach have a lower delay overhead over other codes.

In this paper, novel decimal matrix code (DMC) based on divide-symbol is proposed to provide enhanced memory reliability. The proposed DMC utilize decimal algorithm (decimal integer addition and decimal integer subtraction) to identify errors. The advantage of using decimal algorithm is that the error detection capability is maximize so that the reliability of memory is enhanced. Besides, the encoder-reuse technique (ERT) is proposed to minimize the area overhead of extra circuits (encoder and decoder) without disturbing the whole encoding and decoding processes, because ERT use DMC encoder itself to be part of the decoder

II. PROPOSED DMC

In this section, DMC is proposed to assure reliability in the presence of MCUs through reduced performance overheads, and a 64-bit word is encoded and decoded as an example based on the proposed techniques.

A. Proposed Schematic of Fault-Tolerant Memory

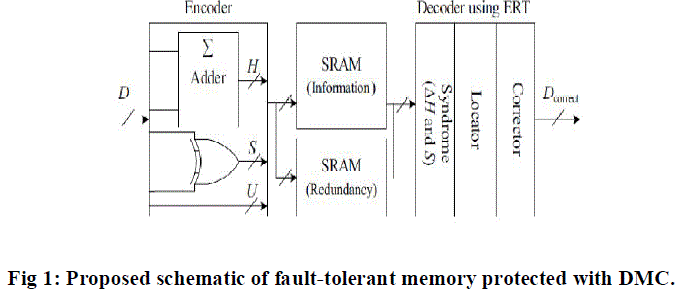
The proposed schematic of fault-tolerant memory is depicted in Fig. First, during the encoding (write) process, information bits D are fed to the DMC encoder, and the horizontal redundant bits H and vertical redundant bits V are obtained from the DMC encoder. When encoding process is completed, the obtained DMC codeword is stored in the memory. If MCUs happen in the memory, these errors can be corrected in the decoding (read) method. Due to the advantage of decimal algorithm, the proposed DMC has high fault-tolerant capability with lower performance overheads. In the fault-tolerant memory, the ERT technique is proposed to decrease the area overhead of extra circuits and will be introduced in the following sections.

B. Proposed DMC Encoder

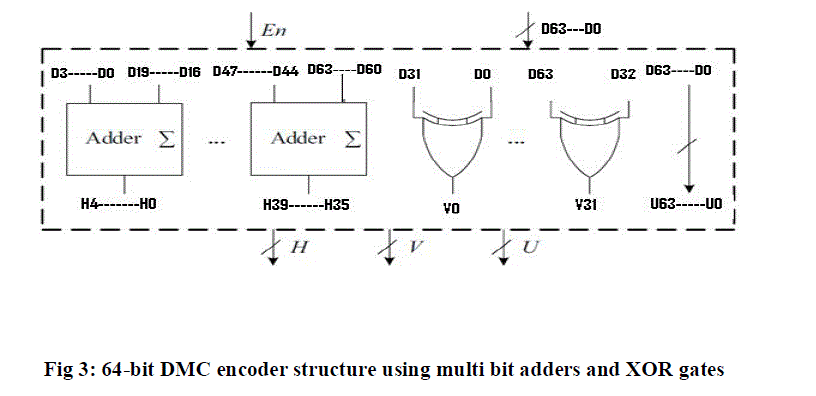
In the proposed DMC, first, the divide-symbol and place-matrix ideas are performed, i.e., the N-bit word is divided into k symbols of m bits (N = k × m), and these symbols are arranged in a k1 × k2 2-D matrix (k = k1 × k2, where the values of k1 and k2 represent the no. of rows and columns in the logical matrix respectively). Second, the horizontal redundant bits H are produced by performing decimal integer addition of selected symbols per row. Here, each symbol is regard as a decimal integer. Third, the vertical redundant bits V are obtained by binary operation among the bits per column. It should be noted that both divide-symbol and arrange-matrix are implemented in logical instead of in physical. Therefore, the proposed DMC does not require changing the physical structure of the memory.

To explain the proposed DMC scheme, we take a 64-bit word as an example, as shown in Fig. 2. The cells from D0 to D63 are information bits. This 64-bit word has been divided into sixteen symbols of 4-bit. k1 = 2 and k2 = 4 have been select simultaneously. H0–H39 are horizontal check bits; V0 through V31 are vertical check bits. However, it should be mentioned that the maximum correction capability (i.e., the maximum size of MCUs can be corrected) and the number of redundant bits are different when the different values for k and m are select. Therefore, k and m must be carefully adjusted to decrease the correction capability and minimize the number of redundant bits. For example, in this case, when k = 2×2 and m = 8, only 1-bit error can be corrected and the number of redundant bits is 80. When k = 4 × 4 and m = 2, 3-bit errors can be corrected and the number of redundant bits is reduced to 32. However, when k = 2 × 4 and m = 4, the maximum correction capability is up to 5 bits and the number of redundant bits is 72. In this paper, in order to enhance the reliability of memory, the error correction capability is first measured, so k = 2 × 8 and m = 4 are utilized to construct DMC.

The horizontal redundant bits H can be obtained by decimal integer addition as follow:

H4H3H2H1H0 = D3D2D1D0 + D19D18D17D16 (1)

H9H8H7H6H5 = D7D6D5D4 + D23D22D21D20 (2)

and similarly for the horizontal redundant bits H14H13H12H11H10, H19H18H17H16H15H16, H24H23H22H21H20, H29H28H27H26H25, H34H33H32H31H30 and H39H38H37H36H35 where “+” represents decimal integer addition. For the vertical redundant bits V, we have

V0 = D0 ^ D31 (3)

V1 = D1 ^ D32 (4)

and similarly for the rest vertical redundant bits

The encoding can be performed by decimal and binary addition operations from (1) to (4). The encoder that computes the redundant bits using multi-bit adders and XOR gates is shown in Figure. In this figure, H39 − H0 are horizontal redundant bits, V31 − V0 are vertical redundant bits, and the remain bits U63 − U0 are the information bits which are directly copied from D31 to D0.

C. Proposed DMC Decoder

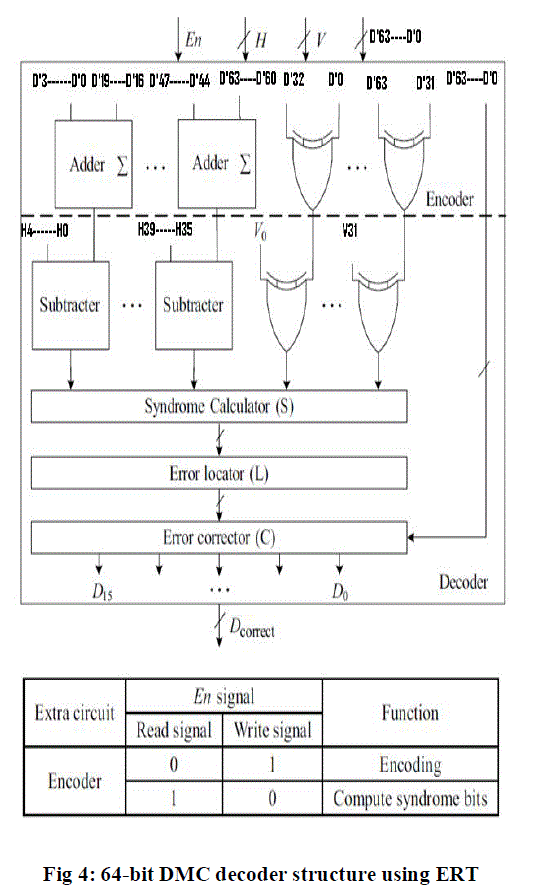
To obtain a word being corrected, the decoding process is required. For example, first, the received redundant bits H4H3H2H1H0’ and V0’-V3’ are generated by the received information bits D’. Second, the horizontal syndrome bits ΔH4H3H2H1H0 and the vertical syndrome bits S3 − S0 can be calculated as follows:

ΔH4H3H2H1H0 = H4H3H2H1H0’ − H4H3H2H1H0 (5)

S0=V0’^V0 (6)

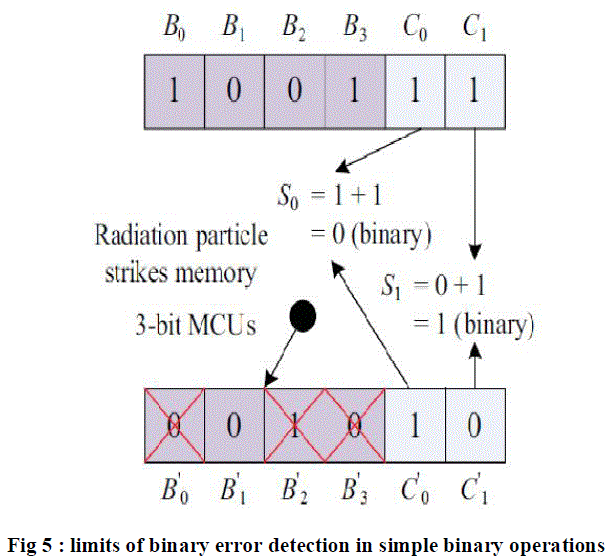
and alike for the rest vertical syndrome bits, where “−” represents decimal integer subtraction. When ΔH4H3H2H1H0 and S3 − S0 are equal to zero, the stored codeword have original information bits in symbol 0 where no errors happen. When ΔH4H3H2H1H0 and S3 − S0 are nonzero, the induced errors (the quantity of errors is 4 in this case) are detected and located in symbol 0, and then the errors can be corrected by

D0correct = D0 ^ S0 (7)

The proposed DMC decoder is depicted in Fig, which is prepared up of the following sub modules, and each executes a particular task in the decoding process: syndrome calculator, error locator, and error corrector. It can be observed from the figure that the redundant bits must be recomputed from the received information bits D’ and compare to the original set of redundant bits in order to obtain the syndrome bits ΔH and S. Then error locator uses ΔH and S to detect and locate which bits some errors occur in. Finally, in the error corrector, these errors can be corrected by inverting the values of error bits.

In the proposed scheme, the circuit area of DMC is minimized with reusing its encoder. This is calling the ERT. The ERT can decrease the area overhead of DMC without disturbing the entire encoding and decoding processes. From Fig, it can be practical that the DMC encoder is also reused for obtaining the syndrome bits in DMC decoder. Therefore, the entire circuit area of DMC can be minimized as a result of using the existent circuits of encoder. Besides, the figure shows the proposed decoder with an allow signal En for deciding whether the encoder needs to be a part of the decoder. In other words, the En signal is used for distinguishing the encoder from the decoder, and it is under manage of the write and read signals in memory. Therefore, in the encoding (write) mode, the DMC encoder is only an encoder to execute the encoding operations. However, in the decoding (read) mode, this encoder is employed for computing the syndrome bits in the decoder. These obviously show how the area overhead of extra circuits can be substantially decreased.

III. SIMULATION RESULTS

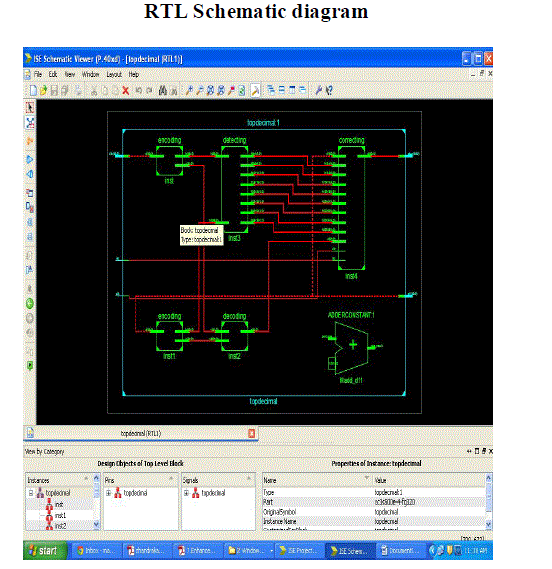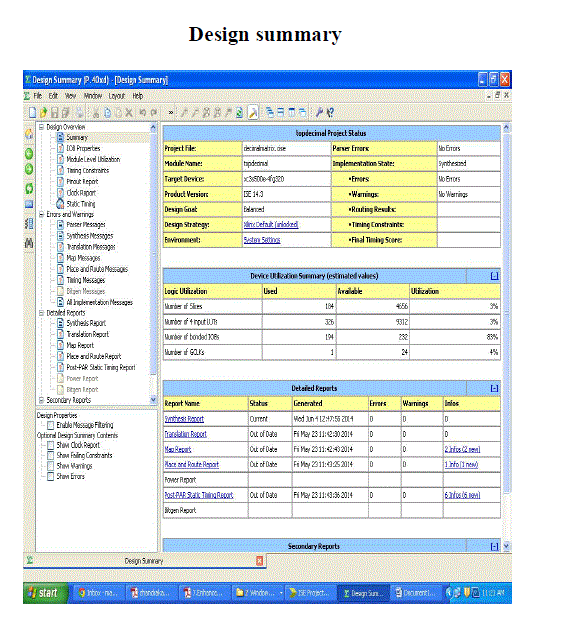IV. CONCLUSION

In the proposed method we were inplemeted the 64-bit decimal matrix code for detection and correction of errors in memories. To avoid MCUs from causing data corruption, more complex error correction codes (ECCs) are widely used to protect memory, but the main problem is that they would require higher delay overhead. newly, matrix codes (MCs) based on hamming codes have been proposed for memory protection. In proposed system increased error detection and correction rate compared to 32-bit decimal matrix code.

Tables at a glance


Table 1	Table 2	Table 3	Table 4	Table 5

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4	Figure 5

References

Jing Guo, Liyi Xiao, Member, IEEE, Zhigang Mao, Member, IEEE, and QiangZhao,”Enhanced memory reliability against multiple cell upsets using Decimal Matrix Code” IEEE Trans. Very Large ScaleIntegr. (VLSI) Syst., vol. 22, no. 1, pp.127-135, Mar 2013.
D. Radaelli, H. Puchner, S. Wong, and S. Daniel, “Investigation of multi-bit upsets in a 150 nm technology SRAM device,” IEEE Trans.Nucl. Sci., vol. 52, no. 6, pp. 2433–2437, Dec. 2005.
E. Ibe, H. Taniguchi, Y. Yahagi, K. Shimbo, and T. Toba, “Impact of scaling on neutron induced soft error in SRAMs from an 250 nm to a 22 nm design rule,” IEEE Trans. Electron Devices, vol. 57, no. 7, pp. 1527–1538, Jul. 2010.
C. Argyrides and D. K. Pradhan, “Improved decoding algorithm for high reliable reed muller coding,” in Proc. IEEE Int. Syst. On Chip Conf., Sep. 2007, pp. 95–98.
A. Sanchez-Macian, P. Reviriego, and J. A. Maestro, “Hamming SEC-DAED and extended hamming SEC-DED-TAED codes through selective shortening and bit placement,” IEEE Trans. Device Mater. Rel., to be published.
S. Liu, P. Reviriego, and J. A. Maestro, “Efficient majority logic fault detection with difference-set codes for memory applications,” IEEETrans. Very Large Scale Integr. (VLSI) Syst., vol. 20, no. 1, pp. 148–156, Jan. 2012.
M. Zhu, L. Y. Xiao, L. L. Song, Y. J. Zhang, and H. W. Luo, “New mix codes for multiple bit upsets mitigation in fault-secure memories,” Microelectron. J., vol. 42, no. 3, pp. 553–561, Mar. 2011.
R. Naseer and J. Draper, “Parallel double error correcting code design to mitigate multi-bit upsets in SRAMs,” in Proc. 34th Eur. Solid-StateCircuits, Sep. 2008, pp. 222–225.
G. Neuberger, D. L. Kastensmidt, and R. Reis, “An automatic technique for optimizing Reed-Solomon codes to improve fault tolerance in memories,” IEEE Design Test Comput., vol. 22, no. 1, pp. 50–58, Jan.–Feb. 2005.
P. Reviriego, M. Flanagan, and J. A. Maestro, “A (64,45) triple error correction code for memory applications,” IEEE Trans. Device Mater. Rel., vol. 12, no. 1, pp. 101–106, Mar. 2012.
S. Baeg, S. Wen, and R. Wong, “Interleaving distance selection with a soft error failure model,” IEEE Trans. Nucl. Sci., vol. 56, no. 4, pp. 2111– 2118, Aug. 2009.
K. Pagiamtzis and A. Sheikholeslami, “Content addressable memory (CAM) circuits and architectures: A tutorial and survey,” IEEE J.Solid-State Circuits, vol. 41, no. 3, pp. 712–727, Mar. 2003.
D. Radaelli, H. Puchner, S. Wong, and S. Daniel, “Investigation of multi-bit upsets in a 150 nm technology SRAM device,” IEEE Trans. Nucl. Sci., vol. 52, no. 6, pp. 2433–2437, Dec. 2005.
E. Ibe, H. Taniguchi, Y. Yahagi, K. Shimbo, and T. Toba, “Impact of scaling on neutron induced soft error in SRAMs from an 250 nm to a 22 nm design rule,” IEEE Trans. Electron Devices, vol. 57, no. 7, pp. 1527–1538, Jul. 2010.
C. Argyrides and D. K. Pradhan, “Improved decoding algorithm for high reliable reed muller coding,” in Proc. IEEE Int. Syst. On Chip Conf., Sep. 2007, pp. 95–98.
A. Sanchez-Macian, P. Reviriego, and J. A. Maestro, “Hamming SEC-DAED and extended hamming SEC-DED-TAED codes through selective shortening and bit placement,” IEEE Trans. Device Mater. Rel., to be published.
S. Liu, P. Reviriego, and J. A. Maestro, “Efficient majority logic fault detection with difference-set codes for memory applications,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 20, no. 1, pp. 148–156, Jan. 2012.
M. Zhu, L. Y. Xiao, L. L. Song, Y. J. Zhang, and H. W. Luo, “New mix codes for multiple bit upsets mitigation in fault-secure memories,” Microelectron. J., vol. 42, no. 3, pp. 553–561, Mar. 2011.
R. Naseer and J. Draper, “Parallel double error correcting code design to mitigate multi-bit upsets in SRAMs,” in Proc. 34th Eur. Solid-State Circuits, Sep. 2008, pp. 222–225.
G. Neuberger, D. L. Kastensmidt, and R. Reis, “An automatic technique for optimizing Reed-Solomon codes to improve fault tolerance in memories,” IEEE Design Test Comput., vol. 22, no. 1, pp. 50–58, Jan.–Feb. 2005.
P. Reviriego, M. Flanagan, and J. A. Maestro, “A (64,45) triple error correction code for memory applications,” IEEE Trans. Device Mater. Rel., vol. 12, no. 1, pp. 101–106, Mar. 2012.
S. Baeg, S. Wen, and R. Wong, “Interleaving distance selection with a soft error failure model,” IEEE Trans. Nucl. Sci., vol. 56, no. 4, pp. 2111– 2118, Aug. 2009.