ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| JAMRUD KHAN 1, Dr. S.MADHAVA KUMAR2, Dr. S. BHARGAVI3 4th sem MTech, Signal Processing, S. J. C. Institute of Technology, Chickballapur, India1 Professor and Hod, Dept of ECE, S. J. C. Institute of Technology, Chickballapur, India2 Professor, Dept of ECE, S. J. C. Institute of Technology, Chickballapur, India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, we have stated the linear underdetermined, instantaneous, convolutive and multiple-output source separation problems in terms of Gaussian processes regression and. The advantages of setting out the source separation problem in terms of GP are numerous. First, there is neither notational burden nor any conceptual issue raised when using input spaces X different from R or Z, thus enabling a vast range of source separation problems to be handled within the same framework. Multi-dimensional signal separation may include audio, image or video sensor arrays as well as geostatistics. Secondly, GP source separation can perfectly be used for the separation of non locallystationary signals. Of course, some important simplifications of the computations as are lost when using non-stationary covariance functions. Thirdly, it provides a coherent probabilistic way to take many sorts of relevant prior information into account.
INTRODUCTION |
| Gaussian processes are commonly used to model functions whose mean and covariances are known.Given some learning points,they enable us to estimate the values taken by the function at any other points of interest. Their main advantages are to provide a simple and effective probabilistic framework for regression and classification as well as an effective means to optimize a modelâÃâ¬ÃŸs parameters through maximization of the marginal likelihood of the observations.For these reasons, they are widely used in many areas to model dependencies between multivariate random variables and their use can be traced back at least to works by Wiener in 1941 . They have also been known in geostatistics under the name of kriging for almost 40 years .A great surge of interest for GaussianProcess (GP) models occurred when they were expressed as a general purpose framework for regression as well as for classification.Their relation to other methods commonly used in machine learning such as multi-layer perceptrons, spline interpolation or support vector machines are now well understood. Source separation is another very intense field of research where the objective is to recover several unknown signals called sources that were mixed together observable mixtures.Source separation problems arise in many fields such as sound processing,telecommunications and image processing.They differ mainly in the relative number of mixtures per source signal and in the nature of the mixing process.The latter is generally modeled as convolutive,i.e. as a linear filtering of the sources into the mixtures. When the mixing filters reduce to a single amplification gain, the mixing is called instantaneous. When there are more mixtures than sources, the problem is called overdetermined and algorithms may rely on beam forming techniques to perform source separation.When there are fewer mixtures than sources, the problem is said to be underdetermined and is notably known to be very difficult. Indeed, in this case there are less observable signals than necessary to solve the underlying mixing equations. Many models were hence studied to address this problem and they all either restrict the set of possible source signals or assign prior probabilities to them in a Bayesian setting. Among the most popular approaches, we can mention Independent Component Analysis [6] that focuses both on probabilistic independence between the source signals and on high order statistics. We can also cite Non-negative Matrix Factorization (NMF) source separation that models the sources as locally stationary with constant normalized power spectra and time-varying energy]. In this study, we revisit underdetermined source separation (USS) as a problem involving GP regression. To our knowledge, no unified treatment of the different underdetermined linear source separation problems in terms of classical GP is available to date and we thus propose here an attempt at providing such a formulation whose advantages are numerous. Firstly, it provides a unified framework for handling the different USS problems as particular cases, including convolutive or instantaneous mixing as well as single or multiple mixtures,secondly,when prior information such as smoothness, local stationarity or periodicity is available, it can be taken into account through appropriate covariance functions, thus providing a significant expressive power to the model. Thirdly, it yields an optimal way in the minimum mean squared error (MMSE) sense to proceed to the separation of the sources given the model. In spite of all their interesting features, GP models come at a high computational cost where n is the number of training points. For many applications such as audio signal processing, this cost is prohibitive. Hence, the GP framework has to come along with effective methods to simplify the computations. |
II. ARCHITECTRAL DESIGN FOR PROPOSED SYSTEM |
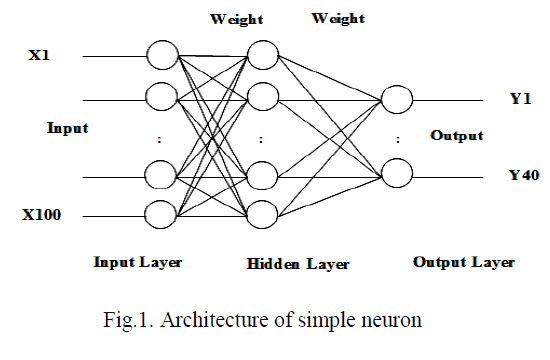 |
III. ANALYSIS OF THE PROJECT |
| Antoine Liutkus, Roland Badeau, Gaël Richard proposed Gaussian process (GP) models are widely used in machine learning to account for spatial or temporal relationships between multivariate random variables. In this paper, we propose a formulation of Underdetermined source separation in multidimensional spaces as a problem involving GP regression. The advantage of the proposed approach is firstly to provide a flexible means to include a variety of prior information concerning the sources and secondly to lead to minimum mean squared error estimates. We show that if the additive GPs are supposed to be locally-stationary, computations can be done very efficiently in the frequency domain. These findings establish a deep connection between GP and non negative tensor factorizations with the Itakura-Saito distance and we show that when the signals are mono dimensional, the resulting framework coincides with many popular methods that are based on non negative matrix factorization and time frequency masking. |
| Mauricio A. A´ lvarez, David Luengo Michalis K. Titsias, Neil D. Lawrence are Interest in multi output kernel methods is increasing, whether under the guise of multitask learning, multi sensor networks or structured output data. From the Gaussian process perspective a multi output Mercer kernel is a covariance function over correlated output functions.One way of constructing such kernels is based on convolution processes (CP). A key problem for this approach is efficient inference. A´ lvarez and Lawrence recently presented a sparse approximation for Cps that enabled efficient inference. In this paper, we extend this work in two directions: we introduce the concept of variational inducing functions to handle potential non-smooth functions involved in the kernel CP construction and we consider an alternative approach to approximate inference based on variational methods, extending the work by Titsias (2009) to the multiple output case. We demonstrate our approaches on prediction of school marks,compiler performance and financial time series. |
| Onur Dikmen, A. Taylan Cemgil are proposed We propose a prior structure for single-channel audio source separation using Non-Negative Matrix Factorization. For the tonal and percussive signals, the model assigns different prior distributions to the corresponding parts of the template and excitation matrices. This partitioning enables not only more realistic modeling, but also a deterministic way to group the components into sources. This also prevents the possibility of not detecting assigning a component and remove the need for a dataset and training. Our method only needs the number ofcomponents of each source to be set, but this does not play a crucial role in the performance. Very promising results can be obtained using the model with too few design decisions and moderate time complexity. |
| Zhiyao Duan¤, Yungang Zhang, Changshui Zhang, Member, IEEE, Zhenwei Shi are proposed Source separation of musical signals is an appealing but difficult problem,especially in the single-channel case. In this paper, an unsupervised single-channel music source separation algorithm based on average harmonic structure modeling is proposed. Under the assumption of playing in narrow pitch ranges, different harmonic instrumental sources in a piece of music often have different but stable harmonic structures, thus sources can be characterized uniquely by harmonic structure models.Given the number of instrumental sources, the proposed algorithm learns these models directly from the mixed signal by clustering the harmonic structures extracted from different frames.The corresponding sources are then extracted from the mixed signal using the models. Experiments on several mixed signals, including synthesized instrumental sources, real instrumental sources and singing voices, show that this algorithm outperforms the general Non negative Matrix Factorization (NMF)-based source separation algorithm, and yields good subjective listening quality. As a side-effect, this algorithm estimates the pitches of the harmonic instrumental sources.The number of concurrent sounds in each frame is also computed, which is a difficult task for general Multi-pitch Estimation (MPE) algorithms. |
IV. PROPOSED ALGORITHMS AND TECHNIQUES USED |
| A. Single Mixture With Instantaneous Mixing: |
| The presentation of GPR given in actually slightly more general than what is usual in the literature. Indeed, it is often assumed that the covariance function of the additive signal is given by KÃÂõ(x,x’ ) =ÃÂñ2δxx’ where δxx’= 1 , x=x’ if and only if and zero otherwise. This assumption corresponds to additive independent and identically distributed (i.i.d.) white Gaussian noise of variance. |
| In our presentation, the additive signal ÃÂõ(x) is a GP itself and is potentially very complex. In any case, its covariance function is given by and the only assumption made is its independence with the signal of interest f(x). A particular example of a model where non trivially depends on and was for example studied in [20]. The results obtained can very well be generalized to the situation where Y is the sum of M independent latent Gaussian processes |
| xÃÂõχ,y(x)=Σm=1 fm(x) |
| with |
| fm~Gp(0,km(x,x’)). |
| In this case, if our objective is to extract the signal corresponding to the source mo,we only need to replace Kf with Kmo and KÃÂõ with Σm≠mo km in GPR. Note that inversion Kf,xx+KÃÂõ,xx is needed only once for the extraction of all sources. Similarly, we can also jointly optimize the hyper parameters of all covariance functions using exactly the same framework as in GPL.We now consider the case of convolutive mixtures of independent GPs. |
| B.Single mixture with convolutive mixing: |
| An important fact, which has already been noticed in some studies such as [2] and [4], is that the convolution of a GP, as a linear combination of Gaussian random variables, remains a GP. Indeed, let us consider some GP |
| f0,m ≈GP(0,K0,m(x,x1)) and let us define |
| fm (x)=∫χ am (χ-z)f0,m(z)dz =(am * f0,m)(x) |
| where am:is a stable mixing filter from f0,m to fm. if the mean function of f0,m is identically 0,the mean function of fm is easily seen to also be identically 0.The covariance function of fm can be computed as Km(x,x1)=E[fm (x)fm (x1)],that is |
| Km (x,x1)=∫χ∫χ am (χ-z) am (χ1-z1) ,K0,m(z,z1)dzdz1 |
| Moreover, if several convolved Gps {fm=( am * f0,m)}m=1…..m are summed up in a mixture, it can readily be shown that the are independent if the are independent. We thus get back to the instantaneous mixing model using modified covariance functions. |
| C. Multiple Output GP: |
| We have for now only considered GPs whose outputs lie in A sizable body ofliterature focuses on possible extensions of this framework to cases where the processes of interest are multiple-valued, i.e., whose outputs lie in RC for CÃÂõN*.In geostatistics for example, important applications comprise the modeling of cooccurrences of minerals or pollutants in a spatial field. First attempts in this direction include the so-called linear model of oregionalization,that considers each output as linear combination of some latent processes. The name of cokriging has often been used for such systems in the field of geostatistics.If the latent processes are assumed to be GPs, the outputs are also Gps. In the machine learning community, multiple-output Gps have been introduced and popularized under the name of dependent GPs.Several extensions of such models have been proposed subsequently and we focus here on the model presented in which is very close to the usual convolutive mixing model commonly used in multichannel source separation. Let {yc}c=1…..c be the C output signals called the mixtures.the convolutive GP model consists in assuming that each observable signal yc is the sum of convolved version of M latent GPs of interest {f0,m~ GP(0,Kom(x,x1))} that will call sources.plus one specific additional term ÃÂõc~ GP(0,KÃÂõc(x,x1) that is often referred to as additive noise.we thus have yc(x)= Σm=1 (acm*f0,m)(x)+ÃÂõc(x). Instead of making a fundamental distinction between c and x, the GP framework allows us to consider that {yc(x)}(c,X)ÃÂõ(1…..c )* x is a singal {yc(x1)}(X 1 )ÃÂõ(1…..c )* x indexed on an extended input space {1……..c}x X .if we assume that the different underlying sources{f0,m}m=1….M are independent, which is frequent in source separation and that the different {ÃÂõc}c=1……C are also independent, two covariance function as |
| Kcc ‘(x,x’ )=ΣKcc ‘ ,m+δcc ’ KÃÂõc)(x,x`) |
| Where Kcc’ '(x,x’)=((acmX ac ''' m )*Ko,m) (x,x`) |
| For any given c the different {fcm=acm *f0,m} are independent and are GPs with mean function 0 and covariance functions Kcc „ ,m (x,x`).fcm will be called contribution of source m to mixture c. we can readily perform source separation on Yc to recover the different {fcm}m=1…M using the standard formalism presented in GPR. Let fcmo be the estimate of fcmo we have |
| fcmo=kcc,mo[mΣm=1 Kcc,m+ Kcc,ÃÂõ,]-1 yc |
| Where Kcc,ÃÂõ is the covariance matrix of the additive signal ÃÂõc and where the covariance matrix Kcc,m is defined as |
| [Kcc,m]x,x` =Kcc,m(x,x`). |
| It is important to note here that even if the sources are the {fo,m}m=1…M many system consider the signals of interest to actually be the different {fcm}c,m. for example in the case of audio source separation, a stereophonic mixture can be composed of several monophonic sources such voice,piano and drums. It is often considered sufficient to be able to separate the different instruments within the stereo mixtures and thus to obtain one stereo signal for each source,rather than trying to recover the monophonic signals. |
V. RESULTS |
| A. single Mixture with convolution Mixing: |
 |
 |
VI. CONCLUSION |
| Gaussian process (GP) models are very popular for machine learning and regression and they are widely used to account for spatial or temporal relationships between multivariate random variables. In this paper, we propose a general formulation of under determined source separation as a problem involving GP regression. The advantage of the proposed unified view is first to describe the different under determined source separation problems as particular cases of a more general framework. Second, it provides a flexible means to include a variety of prior information concerning the sources such as smoothness, local stationarity or periodicity through the use of adequate covariance functions. Third, given the model, it provides an optimal solution in the minimum mean squared error (MMSE) sense to the source separation problem. In order to make the GP models tractable for very large signals, we introduce framing as a GP approximation and we show that computations for regularly sampled and locally stationary GPs can be done very efficiently in the frequency domain. These findings establish a deep connection between GP and non negative tensor factorizations (NTF) with the Itakura-Saito distance and lead to effective methods to learn GP hyper parameters for very large and regularly sampled signals. |
ACKNOWLEDGMENT |
| The authors would like to thank all the anonymous reviewers for the constructive comments and useful suggestions that led to improvements in the quality, presentation, and organization of this paper. We thank M. Alvarez and N. D. Lawrence and Antoine Liutkus and Roland Badeau, for providing their source codes and advice for the experiment implementation. |
References |
|