Keywords
|
| Optimal Power Flow, DE Algorithm, Optimization, Genetic Algorithm, Evolutionary Programming |
INTRODUCTION
|
| Optimal Power Flow (OPF) is a powerful tool in planning and operation of a power system [1]. The OPF problem can be described as the optimal allocation of power system controls to satisfy the specific objective function such as fuel cost, power loss, and bus voltage deviation. The control variables include the generator real powers, the generator bus voltages, the tap ratios of transformer and the reactive power generations of VAR sources. |
| In the OPF problem there is a large constrained like nonlinear non-convex optimization problem [1]. To solve this type of problem consider a number of conventional optimization techniques such as nonlinear programming (NLP) [2], quadratic programming (QP) [3] and linear programming (LP) [4] have been applied. All of these mathematical methods are fundamentally based on the objective function to find the global minimum. The proposed approach is applied to the fuel cost minimization problem of an IEEE 30-bus power system. |
DIFFERENTIAL EVOLUTION ALGORITHM
|
| Differential evolution is proposed by Kenneth V.Price and R. Storn in 1995[5-7] while trying to solve the polynomial fitting problem. It stems from the genetic annealing algorithm which was also developed by Kenneth V.Price troubled by slow convergence of genetic annealing algorithm and the difficulties it faced in determining effective control parameters, Price modified genetic annealing algorithm by using real code with arithmetic operations instead of binary code with Boolean operations. During this process, he discussed the differential mutation operator which was later shown to be the key to the success of differential evolution. |
| Differential evolution is a very simple but very powerful stochastic global optimizer. Since its inception, it has proved to be very efficient and robust technique for function optimization and has been used to solve problems in many scientific and engineering fields. |
| Evolution Mechanism |
| Classic differential evolution involves two stages: initialization and evolution. Initialization generates an initial population P0. Then P0 evolves to P1, P1 evolves to P2… until the termination conditions are fulfilled. While evolving from Pn to Pn+1, the three evolutionary operations, namely, differential mutation, crossoverandselection are executed in sequence |
| Before the population can be initialized, both upper and lower bounds for each parameter must be specified. bL and bU for which subscripts L and U indicate the lower and upper bounds, respectively. For example, the initial value (g = 0) of the jth parameter of the ith vector is |
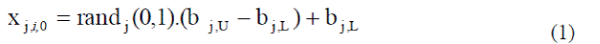 |
| The random number generator randj(0, 1) returns a uniformly distributed random number from within the range [0, 1], |
| i.e. 0 ≤ rand (0,1) j ≤1. The subscript j indicates that a new random value is generated for each parameter. B. Differential Mutation Once initialized, differential evolution mutates and recombines the population to produce a population of Nptrial vectors. Equation (2) shows how to combine three different, randomly chosen vectors to create a mutant vector vi,g |
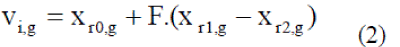 |
| The scale factor F ïÃÆÃŽ(0,1), is a positive real number that controls the rate at which the population evolves. C. Crossover |
| To complement the differential mutation search strategy, differential evolution also employs uniform crossover. In particular differential evolution crosses each vector with a mutant vector |
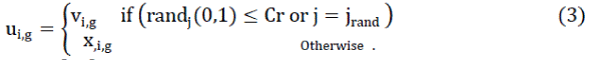 |
| The crossover probability C [0,1] r ïÃÆÃŽ is a user-defined value that controls the fraction of parameter values that are copied from the mutant. |
| D. Selection |
| If the trial vector ui,g has an equal or lower objective function value than that of its target vector Xi,g it replaces the target vector in the next generation. Otherwise the target retains its place in the population for at least one more generation. By comparing each trial vector with the target vector from which it inherits parameters in differential evolution more tightly integrates recombination and selection than other Evolutionary Algorithms |
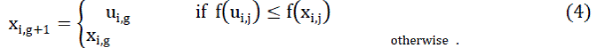 |
| Once the new population is installed, the process of mutation, recombination and selection is repeated until the optimum is located, or a pre specified termination criterion is satisfied, e.g., the number of generations reaches a pre-set maximum gmax. |
OPTIMAL POWER FLOW PROBLEM FORMULATION
|
| Optimal Power flow (OPF) is allocating loads to plants for minimum cost while meeting the network constraints. It is formulated as an optimization problem of minimizing the total fuel cost of all committed plant while meeting the power flow constraints. The variants of the problems are numerous which model the objective and the constraints in different ways. |
| The basic OPF problem can described mathematically as a minimization of problem of minimizing the total fuel cost of all committed plants subject to the constraints. |
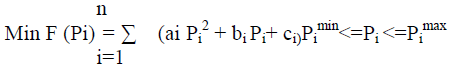 |
| F (Pi)is the fuel cost equation of the „iâÃâ¬ÃŸth plant. It is the variation of fuel cost ($ or Rs) with generated power (MW).The total generation should meet the total demand and transmission loss. The transmission loss can be determined from power flow. |
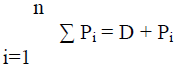 |
| The equality constraints are the nonlinear power flow equations which are formulated as follows |
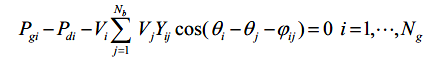 |
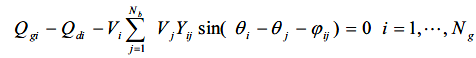 |
| Where Pgi and Qgi are the active and reactive power generations at bus i ,Pdi and Qdi are the active and reactive power demands at bus i ,Vi and Vj are the voltage magnitudes at buses i and j respectively; θi and θj are the voltage angles at buses i and j respectively; ÃÂÃâ¢ij is the admittance angle; Yij is the admittance magnitude; and b N is the total number of buses. |
RESULT AND DISCUSSION
|
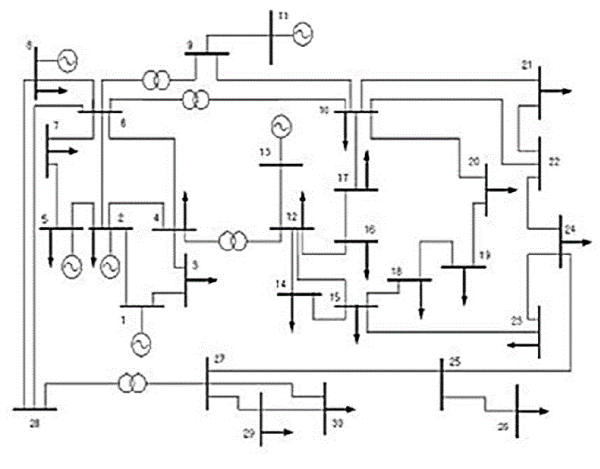
| The proposed DE was tested on the IEEE 30-bus system as shown in Figure. 1 with quadratic generation cost curves for minimizing the total fuel cost. The IEEE 30 bus system consists of 30 buses and 41 branches. It also has a total of 15 control variables as follows: five unit active power outputs, six generator-bus voltage magnitudes, and four transformer-tap settings. |
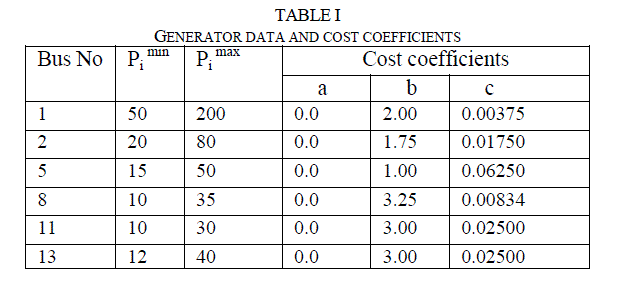
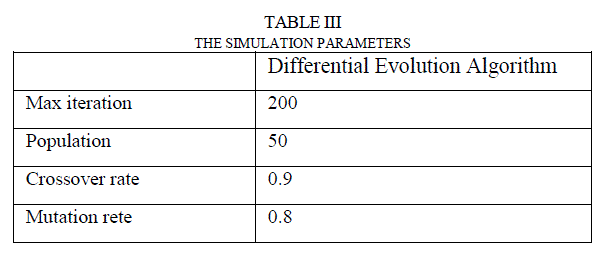
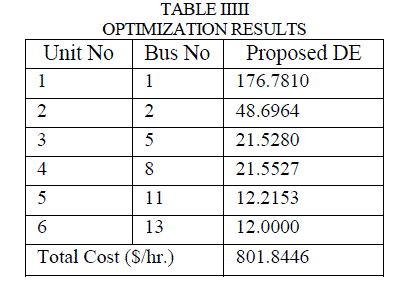
| Table I gives details of the generator data and coefficients of quadratic generation cost curve. Table II gives the simulation parameters and Table III shows the optimization results. |
 |
 |
 |
 |
CONCLUSION
|
| Differential Evolution Algorithm (DE) is a newly proposed population based stochastic optimization algorithm by comparing with other stochastic optimization methods.DE has given good search performance for some hard optimization problems in real power systems. Many research findings indicate that DEgives better performance. In this paper, the DE was proposed and applied to the OPF problem. DE provides better performance than the standard evolutionary algorithms. |
| |
References
|
- J. A. Momoh, J. Z. Zhu, “Improved interior point method for OPF problems,” IEEE Trans on Power System, vol. 14, pp.1114-1120, Aug. 1999.
- M. H. Bottero, E D. Caliana, and A. R. Fahmideh-Vojdani, “Economic dispatch using the reduced hessian,” IEEE Trans on Power Appra. Syst., vol. 101, pp. 3679-3688, Oct. 1982.
- G. E Reid and L. Hasdorf, “Economic dispatch using quadratic programming,” IEEE Trans on Power Appara. Syst., vol. 92, pp. 2015-2023, 1973.
- B. Stott and E. Hobson, “Power system security control calculation using linear programming,” IEEE Trans on Power Appara.Syst., vol. 97, pp. 1713-1731, 1978.
- R. Storn and K. Price,”Minimizing the real functions of the ICECâÃâ¬ÃŸ96 contest by differential evolution”, in Proc. 1996 IEEE on Evolutionary Computation Conf, pp. 842-844.
- K. V. Price, “Differential evolution vs. the functions of the Znd ICEO, in Proc. I9971EEE on Evolutionary CornputationConf , pp.153-157.
- R. Storn, “System design by onstraint adaptation and differential evolution”, IEEE Trans. Evolutionary Computation, vol. 3, pp.22-34, Apr. 1999
- O. Alsac and B. Scott, “Optimal load flow with steady state security,” IEEE Trans on Power Appara. Syst., vol. 93, pp. 745-751, May-June 1974.
|