International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Dynamic Analysis Of Machine Foundation

Piyush K. Bhandari, Ayan Sengupta
Assistant Professor, Dept of Civil Engg, PDVVP COE,Ahmednagar, Maharashtra,India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The analysis and design of machine foundation requires more attention since it involves not only the static loads but also the dynamic loads caused by the working of the machine. The limiting amplitude and operating frequency of a machine are the most important parameters to be considered in analysis of machine foundation. The Elastic half space analogy method with embedment coefficients can be used for coupled modes of vibration to get the natural frequencies and amplitudes of foundation vibrations. With effect to depth of embedment there has been increase in natural frequency but considerable decrease in amplitude of foundation vibrations.

Keywords
Embedment, sliding, rocking, yawing, resonance

INTRODUCTION
The analysis and design of machine foundation requires more attention since it involves not only the static loads but also the dynamic loads caused by the working of the machine. The amplitude of vibration and operating frequency of a machine are the most important parameters to be considered in analysis of machine foundation. With effect to depth of embedment there may increase in natural frequency but considerable decrease in amplitude of vibration of foundation.

BACKGOUND AND PURPOSE
The machine foundations should be designed such that the dynamic forces of machines are transmitted to the soil through the foundation in such a way that all kinds of harmful effects are eliminated. In past the calculations involved multiplying of static loads i.e. vertical loads with an estimated dynamic factor and result was treated as increased static load. Even then harmful deformations during operation were observed.
Hence new theoretical procedures are developed for calculating the dynamic response of foundations. Therefore suitability of machine foundation depends not only on the forces to which they are subjected but also on their behavior when exposed to dynamic loads.

MACHINE FOUNDATION TYPES
A. Block type foundation
It is provided for compressors and reciprocating machine. It consists of a pedestal resting on footing.
B. Box type foundation
Similar to block foundation, but are relatively lighter so its natural frequency increases. This foundation consists of hollow concrete block or a box acting as a footing to support the machinery.
C. Table-type foundation
They are quite complex and consists of a system of wall columns, beams and slabs. It includes large turbine-driven equipment such as electric generators which requires elevated supports. It allows ducts, piping and ancillary items to be located below the equipment.

DESIGN CRITERIA
The basic goal in the design of a machine foundation is to limit its motion i.e. amplitudes. Allowable amplitudes depend on the speed, location and function of the machine. Other limiting dynamic criteria affecting the design may include avoiding resonance and excessive transmissibility to the supporting soil or structure.
Machine foundation should insure following criteria to insure its safe and efficient working all over its life period.
1. It should be safe against shear failure.
2. It should not settle excessively.
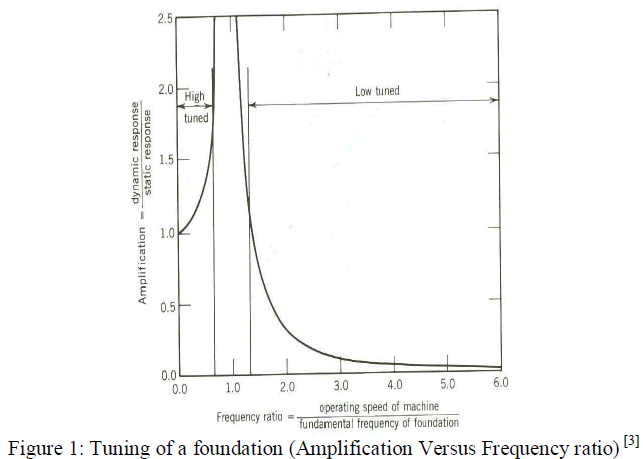image
3. There should be no resonance, i.e. the natural frequency of the machine foundation-soil system should not coincide with the operating frequency of the machine. Frequency ratio should not be within 0.8 to 1.4
4. The amplitudes of motion at operating frequencies should not exceed the limiting amplitudes, which are generally specified by machine manufacturers.
A. Degrees of freedom of a rigid block foundation
A typical concrete block undergoes rigid-body displacements and rotations. Under the action of unbalanced forces, the rigid block undergoes vertical, lateral, longitudinal, rocking, pitching and yawing oscillations.
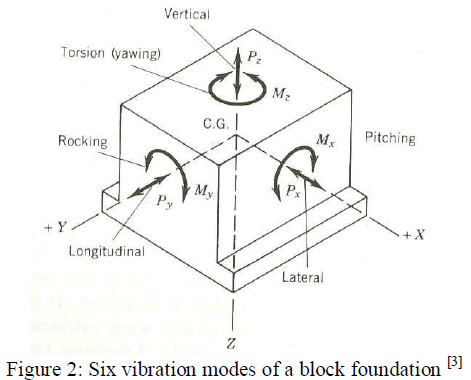image
Translation along the Z axis and rotation about the Z axis occur independently of any other motion. However, translation about the X axis (or Y axis) and rotation about the Y axis (or X axis) are coupled motions.
B. Soil profile and dynamic soil properties
Satisfactory design of a machine foundation needs information of soil profile, depth of different layers, physical properties of soil and ground water level. Dynamic shear modulus of a soil is generally determined from laboratory or field tests.
The soil properties needed in analysis of foundation are:
1. Dynamic moduli, Young’s modulus E and Shear modulus
2. Poisson’s ratio μ.
3. Dynamic elastic constants such as coefficient of elastic uniform compression Cu, coefficient of elastic uniform shear Cτ, coefficient of elastic non-uniform compression Cφ and coefficient of elastic non-uniform shear Cψ.
4. Damping ratio ξ.

METHOD OF ANALYSIS
The problem of a rigid block foundation resting on the ground surface therefore be represented in a reasonable manner by a spring-mass-dashpot system. The equivalent soil spring represents the elastic resistance of the soil below the base of the foundation. The dashpot represents the energy loss or the damping effect. For coupled modes of vibration, as for combined rocking and sliding, two degree-of-freedom model is used.
The methods considered for vibration analysis of surface mounted machine foundations are:
A. Linear elastic spring method [5]
B. Elastic half-space analogs method [3]
A. Linear Elastic Spring method (Barkan, 1962)
It is also referred as IS code method. In this method soil is assumed to be replaced as elastic springs. The effect of damping and participating soil mass is neglected. Since the zone of resonance is avoided in designing machine foundations, the effect of damping on amplitudes computed at operating frequency is also small.
B. Elastic Half Space Analog Method
The elastic half space theory can be used to get the values of equivalent soil springs and damping then make use of theory of vibrations to determine the response of the foundation. This approach is apparently more rational, but relatively more complicated. The equivalent soil spring and damping values depend upon the; soil type and its properties, geometry and layout of the foundation and nature of the foundation vibrations occasioned by unbalanced dynamic loads.
C. Arya, Neill and Pincus method
The method proposed by author Arya, Neill and Pincus [4] from extension of work of Whiteman (1972) is used for dynamic analysis of embedded machine foundation using elastic half analogy method and embedment coefficients. The embedment of the foundation results in an increased contact between the soil and the vertical faces of the foundation.
The elastic half-space method for calculating the response of surface foundations was developed by Richart (1970). For embedded foundation Arya, Neill and Pincus method has been considered where embedment coefficients are used to get displacement and frequencies values for coupled modes of vibration
The solution is based upon the following assumptions:
1) The footing is rigid.
2) The footing is cylindrical.
3) The base of the footing rests on the surface of a semi-infinite elastic half-space.
4) The soil reactions at the base are independent of the depth of embedment.
image
image
The values of equivalent spring and damping for the embedded foundation for the vertical, sliding, rocking and torsional modes are given in the Tables 1 and 2[4]. The vibratory response of the foundation are calculated using the appropriate equations as for the elastic half-space analog for the surface foundations and multiplying the spring stiffness and damping values with the corresponding values embedment coefficient (factor) for the embedded foundations.
For a given foundation having circular base the values are calculated which can be further converted for rectangular footing by using suitable equivalent footing radius as conversion factor. The natural frequency and resultant amplitude in individual vibration mode as as well as coupled vibration are calculated to get resultant amplitude in vertical and horizontal direction.
D. Problem Statement
A reciprocating machine of size 4.0 m x 3.0 m x 3.5 m high mounted on foundation on sandy soil having φ =35˚and γsat= 15kN/m3. Its vibrating speed is 250 rpm generates maximum vertical unbalanced force 2.5 KN, torque about Z-axis 4.0 KN-m and maximum horizontal unbalanced force 2.0 KN at a height of 0.2 m above the top of the block. Block resonance test on soil gave Coefficient of elastic uniform compression, Cu= 3.62×104 KN/m3, Dynamic shear modulus, G =1.10×104 KN/m2, Poisson’s ratio, μ = 0.35, Young’s modulus of elasticity, E = 2.98×104 KN/m2. The natural frequencies and amplitude for surface and embedded foundation need to be computed and reviewed to get effect of embedment on displacement and frequency values.
E. Results & Discussion:
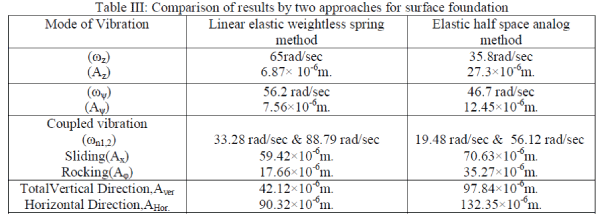
I) Vibration analysis of surface machine foundation:
image
II) Vibration analysis of embedded machine foundation: With variation in depth of embedment, the vibration analysis of machine foundation is performed using Arya, Neill and Pincus method i.e. by using Lysmer and Richart model along with embedment coefficients to study effect of embedment.
The depth of embedment is varied in increasing order with difference of 0.5m. The depths taken are 0.5m, 1.0m, 1.5m, 2.0m, 2.5m, 3.0m and 3.5m i.e. total embedment.
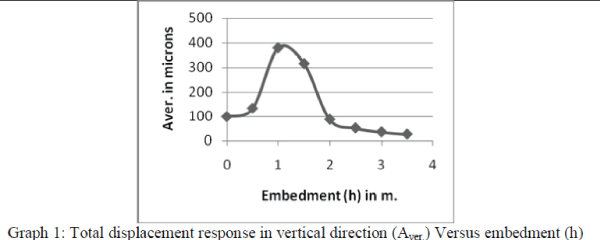
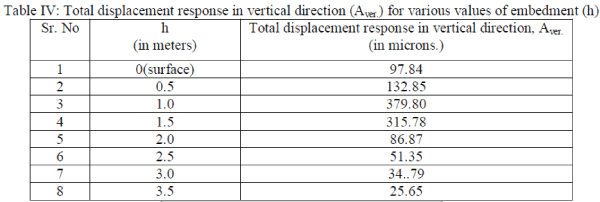
1. Considering the plot of total displacement response in vertical direction (Aver.) to embedment (h).
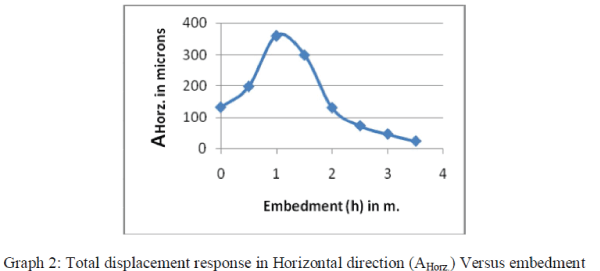
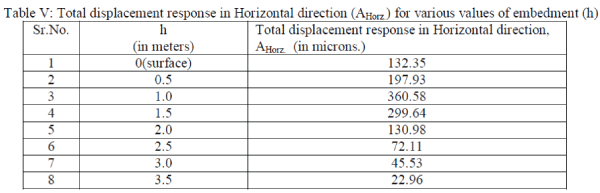
image
2. Considering the plot of total displacement response in Horizontal direction (AHorz.) to embedment (h).
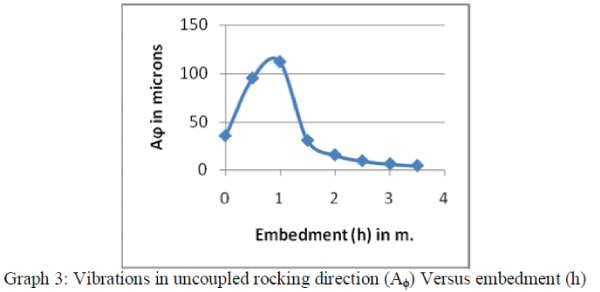
image
image
3. Considering the plot of vibration in uncoupled rocking direction (Aφ) to embedment (h).
image
image
F. Discussions on work
1. The I.S. code method commonly known as Barkan’s method is widely used in machine foundation design for finding out the maximum amplitude as well as frequency in various modes of vibration. But it is associated with various limitations and drawbacks.[8]
2. In present work comparison in made between IS code method with Elastic half space analog method for surface block foundation handling reciprocating machine with maximum operating speed 250 rpm. The comparison has clearly revealed that former method gives less value of amplitude but higher value of frequency that the later method.
The difference in values in mainly due the calculation method and laboratory procedure used to determine value of shear modulus G used in the formulae. For IS code method Block resonance test is used to calculate value of soil constants and same values are also used for elastic half space method, whereas wave propagation test must be used for later method. [5]
3. By using Arya, Neill and Pincus method the embedment coefficients are multiplied to spring constant and damping ratio to get effect of embedment on values of frequency and amplitude using Lysmer and Richart models[4],[6]
4. The successive graphs plotted clearly indicate variation in values due to increasing depth of embedment. The results are as follows.
(a) With increase in depth (i.e. embedment, h) there is decrease in value of Total vibration response of foundation in vertical direction (Aver.) (Graph 1). This indicates that foundation should be embedded as deep as possible to take benefit of adjoining confining soil to carry energy waves to reduce the total vibration response. But initially at depth of h equal to 0.5m, 1.0m and 1.5m, it shows sudden increase in amplitude of vertical vibration. It is mainly because vertical vibration is due to combined effect of vertical and rocking response, as seen it in the formula. If natural frequency of foundation in rocking response (ωφ) is considered, it is observed that at depths of 0.5m, 1.0m and 1.5m the natural frequency of foundation (ωφ) is very close to operating frequency of machine (ω). This creates possibility of resonance and this cause increase in amplitude. From Figure 1. Amplification versus frequency ratio ‘r’, it is observed that as ωφ approaches to ω value of ‘r’ frequency ratio becomes nearly equal to 1 then there is possibility of resonance i.e. increase in amplitude of vibration exceeding permissible value of 150 microns. This is undesirable for foundation.
This condition is arising because of embedment of foundation. For surface foundation the foundation is free to oscillate in vertical, horizontal and rocking mode. But after introduction to embedment the surrounding soil restricts free oscillation in rocking mode due to confinement. This has cause decrease in natural frequency for rocking vibration and it becomes nearly equal to operating frequency of machine. This is going to cause resonance in foundation vibration which will affect life of foundation. Hence either foundation should be embedded deep in soil or its base area should be increased to avoid value of frequency ratio becoming equal to 1.
(b) With increase in depth (i.e. embedment, h) there is decrease in value of Total vibration response of foundation in Horizontal direction (AHorz.). (Graph 2) and also same is for rocking vibration, there is decrease in amplitude with increase in embedment. The reason is due to possibility of resonance in early stage of embedment. Hence foundation need to embedded deep in ground.
(d) With increase in depth (i.e. embedment, h) there is increase in value of natural frequency in foundation vertical direction (ωz.), horizontal direction (ωx.) and in rocking direction (ωφ.). The increase in value of natural frequency clearly indicates that as the depth of embedment goes on increasing from surface foundation to deep in ground the effect is it will help to reduce the displacement response in all modes of vibration.

CONCLUSION
The paper includes machine foundation types and its behavior under dynamic loading in general and response of embedded machine foundation in particular. The analysis problem has been studied about a reciprocating machine installed on block foundation placed on ground surface as well as when it is embedded in ground at different depths by Elastic half space analog method and embedment coefficients. The values of frequencies and amplitudes in different modes of vibrations are compared to study effects of embedment of foundation on its performance.
Following are the conclusions drawn which confirm the observations and discussions.
1. The values of amplitudes uncoupled vibrations in sliding as well as in rocking modes are less as compared to coupled vibrations.
2. In case of embedment of foundation for shallow depth resonance has been occurred for ‘present dimensions of foundation’, this concludes that as natural frequency approaches to operating frequency, frequency ratio becomes nearly equal to one and it is condition of resonance i.e. amplitude rises suddenly and may reach infinity. This affects service life of foundation.
3. At greater depth of embedment the total vertical and horizontal vibration response goes on decreasing.
4. The natural frequency of foundation is seen to be increasing with increase in depth of embedment of foundation.
5. Therefore the increase in depth of embedment causes increase in values of spring constants or natural frequencies and reduces amplitudes of vibration which is beneficial for machine foundation.
6. For practical purposes the dimensions of base area are important and also the shape of foundation.

References