S Kiruba Seeni Anantham1*, Esther Christopher Das1, S Dominic Rajkumar2
1Department of Mathematics, ST Andrew’s College, Uttar Pradesh, India
2Department of Botany, ST Andrew’s College, Uttar Pradesh, India
Received: 27-April-2023, Manuscript No. JSMS-23-97131; Editor assigned: 02-May-2023, Pre QC No. JSMS-23-97131 (PQ); Reviewed: 16- May-2023, QC No. JSMS-23-97131; Revised: 01-September- 2023, Manuscript No. JSMS-23-97131 (R); Published: 29-September-2023, DOI: 10.4172/JSMS.9.3.014
Citation: Anantham SKS, et al. Dynamic Behavioral Analysis of Two Plant Species through Mathematical Model. Stats Math Sci. 2023;09:014.
Copyright: © 2023 Anantham SKS, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this paper the dynamic behaviour of two competing plant species is analyzed through mathematical model. The present approach is able to overcome the unrealistic theoretical basis and simplifies the interspecific competition processes of classical Lotka-Volterra competition equations. We discuss the interspecific competition between two plant species, namely Christella dentata and Christella parasitica in Kushmi jungle forest, Northern region of India. We obtained steady state solution, which were characterized by linearization method and analyzed.
Mathematical model; Interspecific competition; linearization method; Lotka-Volterra competition
Over the years it has been difficult to predict the consequences of population growth of plant species and this posed a problem to ecologist. Mathematical modeling has been a tool used by ecologist and has provided a reasonable approach to ecologist in the study of interaction of species. The remarkable variety of dynamical behaviors exhibited by many species (plants, insects and animals) has simulated great interest in the development of dynamical system models of populations [1,2]. In the 20th century Lotka and Volterra derived Lotka-Volterra model for species competition. This model included the competition between two and more species called Interspecific competition. This model is of interest to ecologist because of its biologically meaningful parameters [3,4].
The competition between two different species at the same genus level, Christella dentata and Christella parasitica in Kushmi jungle, Northern part of India has been studied in the present work. Similar such work has also been done by Nevile. They have studied the complex interaction between two plant species in a harsh climate [5,6]. Yubin have worked on how to stabilize a mathematical model of interactions of n species population. Mark have considered mathematical model for biological invasion. Freekelston studied the determinants of the abundance of invasive annual weed. The dynamic of an annual pasture community was described from a five-year experimental and monitory study. Christian studied the plant competition experiments with variable plant density based on three published data sets [7,8].
Mathematical formulation of model
This is described by the following differential equations. The two species Lotka-Volterra competition model is followed in this work for having density dependent growth and this makes it more realistic. The interaction of two species competing for some limited resources leads both plant species to competition, especially interspecific competition. A model can be used as an estimator of some parameter [9,10]. This approach carried the assumptions that the dynamics of the healthy meta populations can represent those of the endangered one and that the threats to the latter were external to population dynamics. Most dynamical system models which arise in practice are not amenable to exact solutions by known technique. Presently we follow the techniques which can be applied to analysis of almost any dynamical system model. These methods can provide important qualitative information about the behaviour of dynamical systems [11,12].
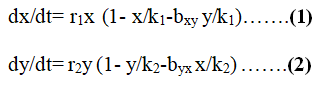
Where, x (t) is density of plant Christella parasitica at time t, y (t) is density of Christella dentata at time t.
r1 and r2 are intrinsic growth rates, k1 and k2 are carrying capacity of Christella parasitica and Christella dentata respectively.
bxy measures competitive effect of y on x and byx measures competitive effect of x on y.
Steady-State Solution (SSS)

Characterization of steady-state solution
In order to investigate the stability of steady-state solution, we have linearlise competitive model (1) and (2) by obtaining Jacobian matrix. The characteristic equation is given by:
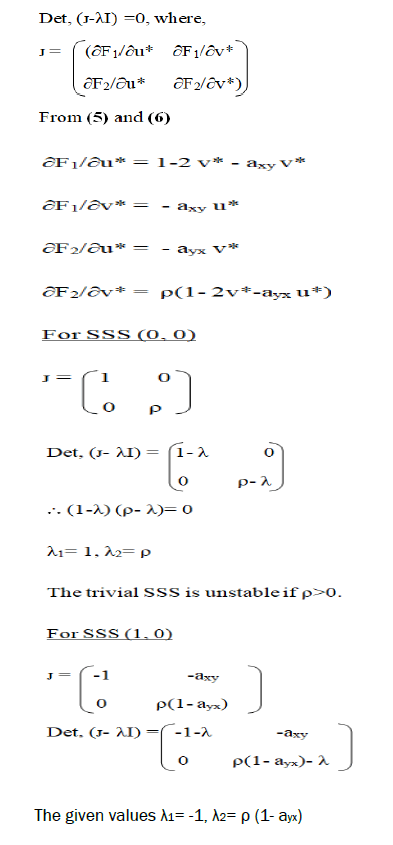
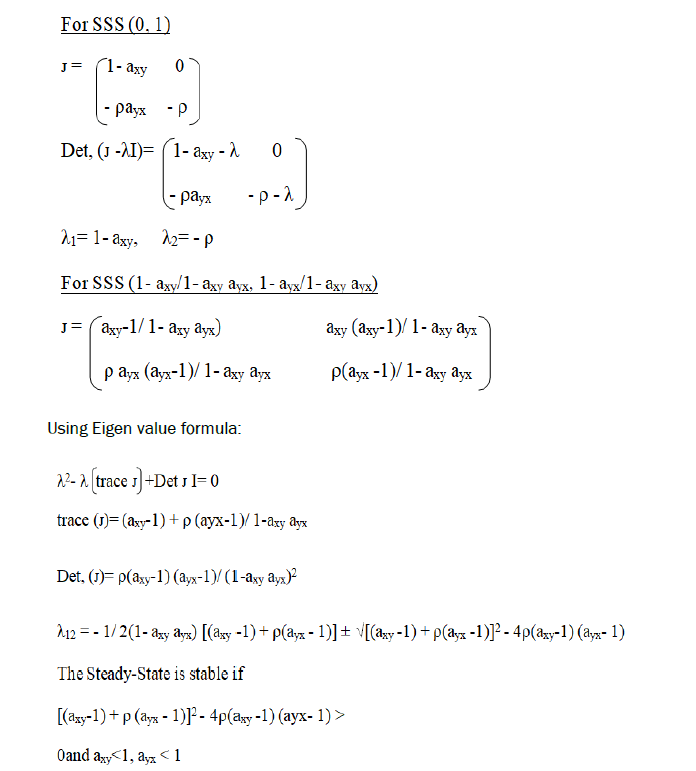
We got three stable solutions which are dependent on the axy, ayx.
•axy>1, ayx<1, growth of Christella parasitica and extinction of Christella dentata.
•axy<1, ayx>1, then extinction of Christella parasitica and growth of Christella dentata.
•axy<1, ayx<1, coexistence of two species.
Indeed, mathematical model has provided a good and reasonable approach to ecologist in the study of the interaction of plant species. Having considered the Lotka Volterra competition model we obtained four steady state solutions which were characterized using the Linearization method. We can say that the size of the parameters axy, ayx, ρ will determine the stability of the steady state solutions.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]