Dynamic Modeling, Simulation and Control of MIMO Systems

Abstract

Designing control systems for complete plants is the ultimate goal of a control designer. The problem is quite large and complex. It involves a large number of theoretical and practical considerations such as quality of controlled response; stability; the safety of the operating plant; the reliability of the control system; the range of control and ease of startup, shutdown, or changeover; the ease of operation; and the cost of the control system. The difficulties are aggravated by the fact that most of the industrial and chemical processes are largely nonlinear, imprecisely known, multivariable systems with many interactions. The measurements and manipulations are limited to a relatively small number of variables, while the control objectives may not be clearly stated or even known at the beginning of the control system design. Thus, the presence of process input-output time delay of different magnitude in multi-input-multi-output systems have drawn attention to research as the processes are difficult to control. Increase in complexity and interactions between inputs and outputs yield degraded process behavior.

Keywords

multivariable systems, interaction, control system design, nonlinear

INTRODUCTION

In recent years all the methodologies adapted to solve for the parameters of individual controllers in which the loop interactions are taken into account have not guaranteed a solution. In addition, the extension for higher dimensional systems seems difficult because of the complicated and non-linear computation. It has been found that the independent design of decentralized controllers based on model based method is simple and effective only for low dimensional processes. For high dimensional processes this design has to be more conservative due to the inevitable modeling errors encountered in formulation.

To overcome all these drawbacks and to include interactions in the control design, a novel method based on the equivalent transfer function method (ETF) is proposed. By considering four combination modes of gain and phase changes for a particular loop when all other loops are closed, this equivalent transfer function can effectively approximate the dynamic interactions among loops. Consequently, the design of decentralized controller for MIMO processes can be converted to the design of single loop controllers. The method is simple, straightforward, easy to understand and implement. Several multivariable industrial processes with different interaction characteristics are employed to demonstrate the effectiveness and simplicity of the design method compared to the existing methods.

CONTROLLER DESIGN METHODOLOGIES:

There are three major controller designs that are available. They are mainly

a) Centralized controller

b) Decentralized controller and

c) Decoupler

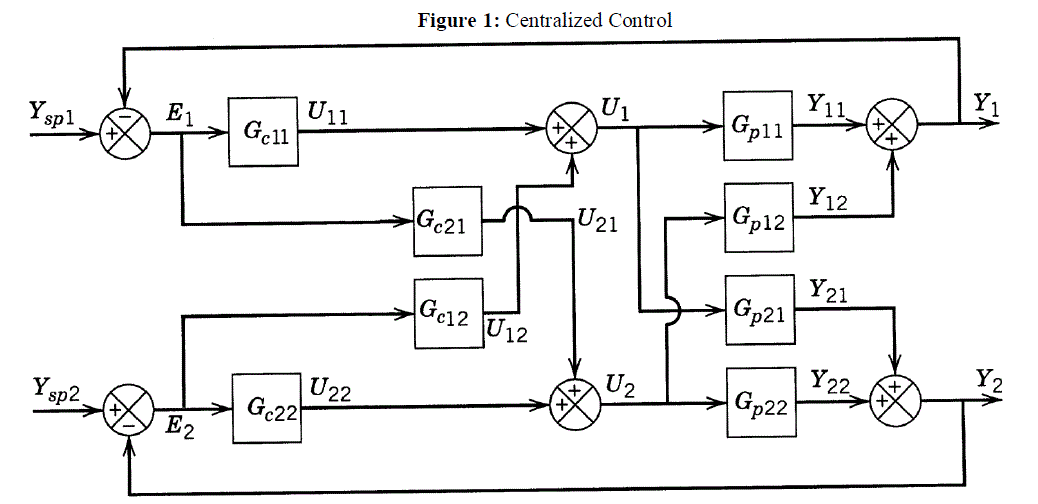
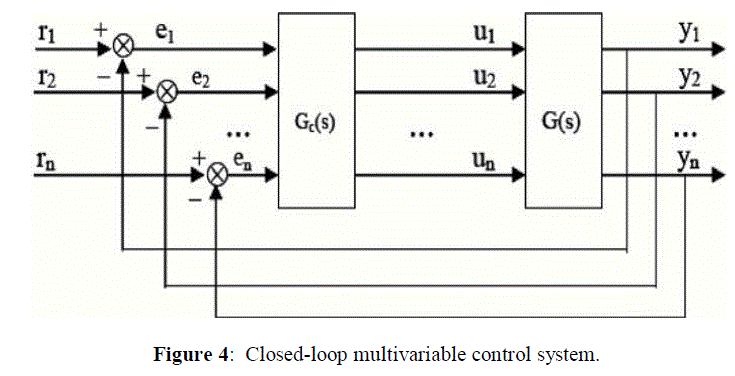
Of all the three configurations discussed above, the centralized controller is not used very widely because of the complexity and time constraints in computation. In addition to it the design is less transparent and can be damaging the entire plant during failures, thus not being highly reliable. The figure below shows the block diagram of a decentralized controller and with its representation.

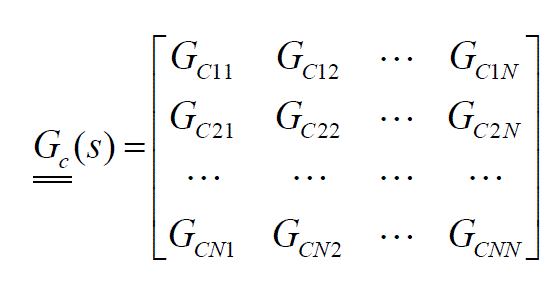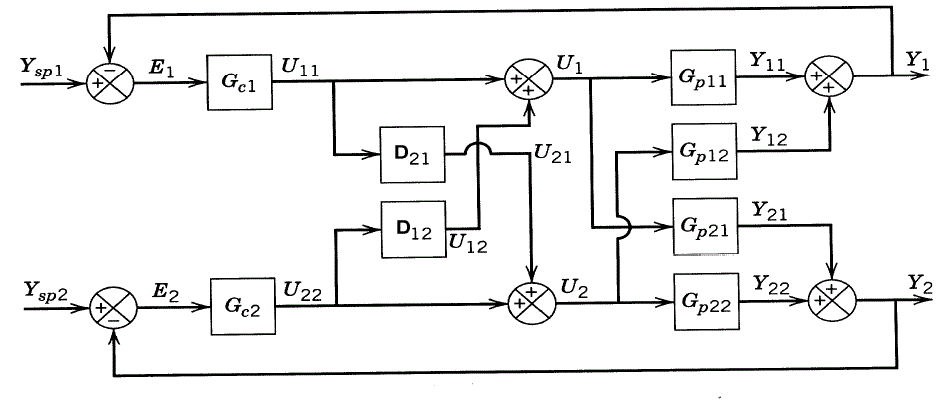
The decoupler though profitable and realistic is also very complex and degrades the load rejection. It has to be applied carefully and is often recommended only for the servo operations. The Figure 2 shows the block diagram for the decoupler.

The Decentralized controllers are widely used because of their simplicity in hardware, design and tuning simplicity, flexibility in operation and maintenance.

The block diagram of the decentralized controller is shown in figure 3. The decentralized controller is represented as

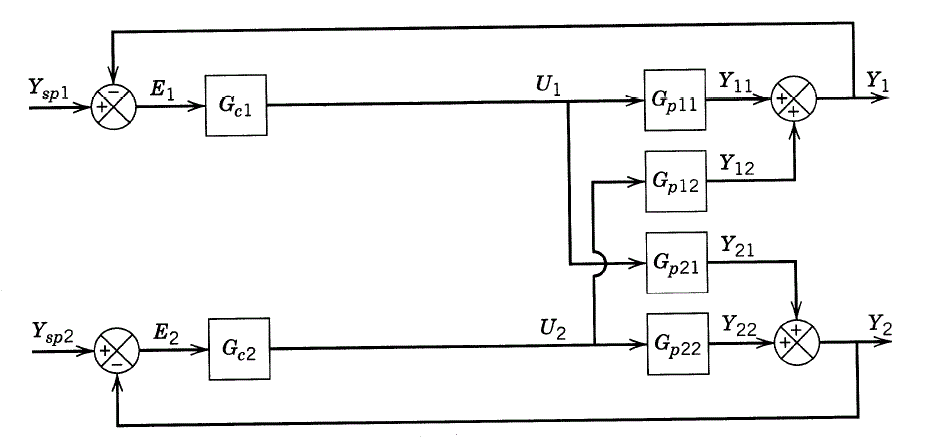All the three controller configurations are being shown for a 2x2 system with interactions. The decentralized controllers consist of multi loop SISO controllers with one control variable paired with one manipulated variable. The major idea in this design approach is that the SISO controllers should be tuned simultaneously with the interactions in the process taken into account.

PROCEDURE FOR DECENTRALISED CONTROLLER DESIGN

Most industrial control systems use the multi loop SISO diagonal control structure.

It is the most simple and understandable structure. Operators and plant engineers can use it and modify it when necessary. It does not require an expert in applied mathematics to design and maintain it. In addition, the performance of these diagonal controller structures is usually quite adequate for process control applications. In fact, there has been little quantitative unbiased data showing that the performances of the more sophisticated controller structures are really any better! The slight improvement is seldom worth the price of the additional complexity and engineering cost of implementation and maintenance.

A number of critical questions must be answered in developing a control system for a plant. What should be controlled? What should be manipulated? How should the controlled and manipulated variables be paired in a multivariable plant? How do we tune the controllers? The procedure discussed in this chapter provides a practical approach to answering these questions. It was developed to provide a workable, stable, simple SISO system with only a modest amount of engineering effort. The resulting diagonal controller can then serve as a realistic benchmark, against which the more complex multivariable controller structures can be compared. The limitations of the procedure should be pointed out. It does not apply to open loop-unstable systems. It also does not work well when the time constants of the transfer functions are quite different, i.e., some parts much faster than others.

The fast and slow sections should be designed separately in such a case. The procedure has been tested primarily on realistic distillation column models.

This choice was deliberate because most industrial processes have similar gain, dead time, and lag transfer functions. Undoubtedly, some pathological transfer functions can be found that the procedure cannot handle. But we are interested in a practical engineering tool, not elegant, rigorous, all-inclusive mathematical theorems.

The steps in the procedure are summarized below. Each step is discussed in more detail in later sections of this chapter.

1. Select controlled variables. Use primarily engineering judgment based on process understanding.

2. Select manipulated variables. Find the set of manipulated variables that gives the largest minimum singular value of the steady-state gain matrix.

3. Eliminate unworkable variable pairings. The pairing can be done with RGA ERGA or using NI indices.

4. Find the best pairing from the remaining sets.

a. Tune all combinations using a efficient tuning methodology.

b. Select the pairing that gives the lowest-magnitude closed loop regulator transfer function.

EFFECTIVE TRANSFER FUNCTION

COMPUTATION OF ETF

Consider an open loop stable multivariable system within inputs and n outputs as shown in Fig. 1, where ri, i =1, 2, . . . ,n, are the reference inputs; ui, i= 1,2,. . . ,n, are the manipulated variables; yi, i = 1,2,. . . ,n, are the system. Outputs, G(s) and Gc(s) are process transfer function matrix And decentralized controller matrix with compatible dimensions, expressed by

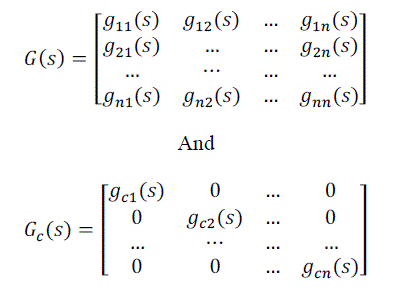respectively.

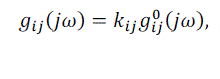Where and kij and gij0(jω) ,are steady state gain and normalized transfer function of ,i.e., gij0 (0) = 1 , respectively. The interaction among individual loop is described by ERGA, the main result of ERGA is summarized as follows. Define of a particular transfer function as

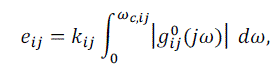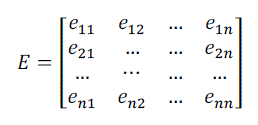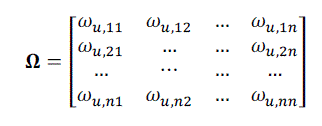Are the steady state gain and the critical frequency array, respectively. Since eij is an indication of energy transmission ratio for loop yi − uj, the bigger the eij value is, the more dominant of the loop will be.

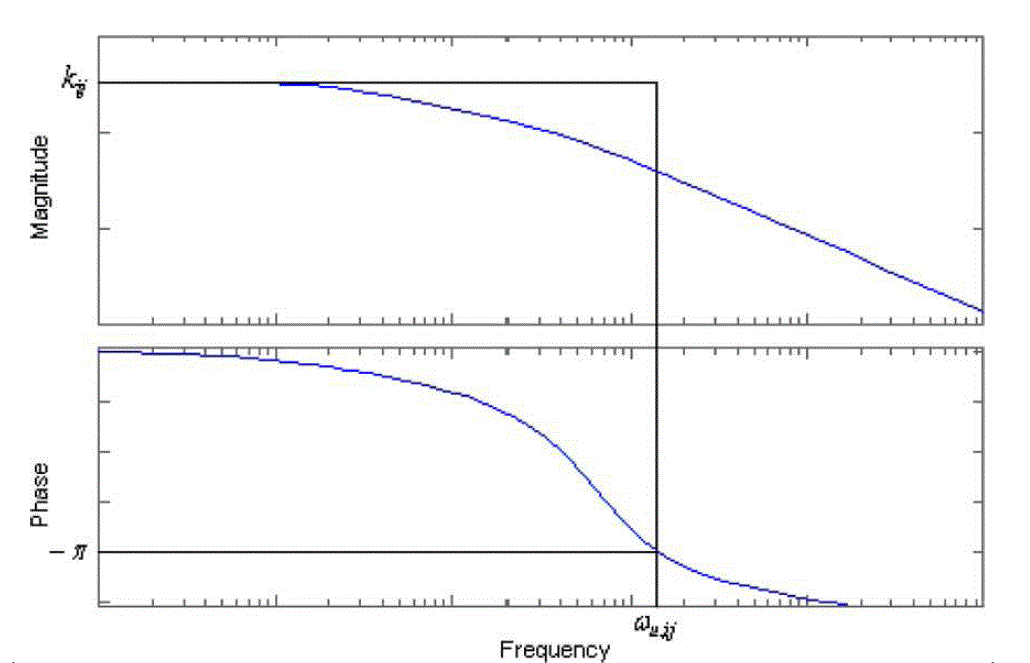Similar to the definition of relative gain , the effective relative gain,Φij between output variable Yi and input variable Uj,is define as the ratio of two effective energy transmission ratio:

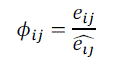where eij is the effective energy transmission ratio between output variable yi and input variable uj, when all other loops are closed. When the effective relative gains are calculated for all the input/output combinations of a multivariable process, it results in an array, ERGA, which can be Calculated by

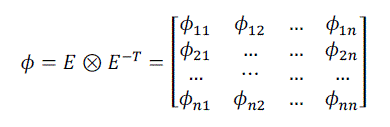The introduction of energy transmission ratio is to mathematically represent the effectiveness of a control loop which is affected by two key factors, i.e., the steady state gain of the transfer function reflecting the effect of the manipulated variable uj, to the controlled variable yi and the response speed reflecting the sensitivity of the controlled variable yi to the

manipulated variable uj,and, consequently, the ability to reject the interactions from other loops. Since ERGA is a relative measure, using the multiplication of the two parameters to approximate the energy transmission ratio in Φij can simplify the calculation while captures the key elements in a multivariable control system.

The introduction of energy transmission ratio is to mathematically represent the effectiveness of a control loop which is affected by two key factors, i.e., the steady state gain of the transfer function reflecting the effect of the manipulated variable uj,to the controlled variable yi and the response speed reflecting the sensitivity of the controlled variable yi to the manipulated variable uj, and, consequently, the ability to reject the interactions from other loops. Since ERGA is a relative measure, using the multiplication of the two parameters to approximate the energy transmission ratio in Φij can simplify the calculation while captures the key elements in a multivariable control system. The ERGA is used to determine the best variable paring. In the following sections, we will employ this interaction measure to develop effective transfer functions (ETFs) under decentralized control structure

EFFECTIVE TRANSFER FUNCTION

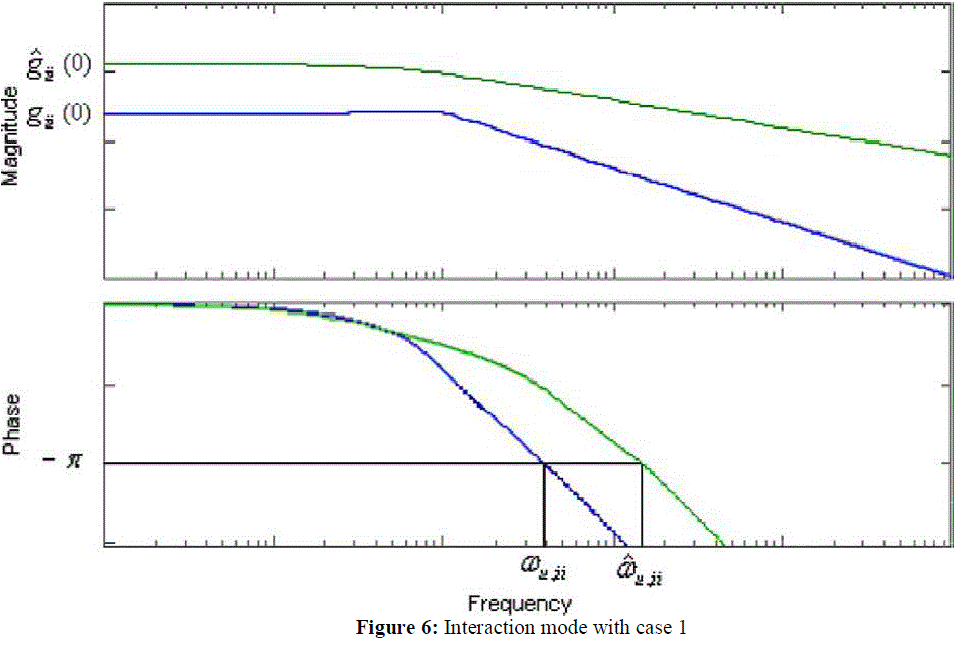
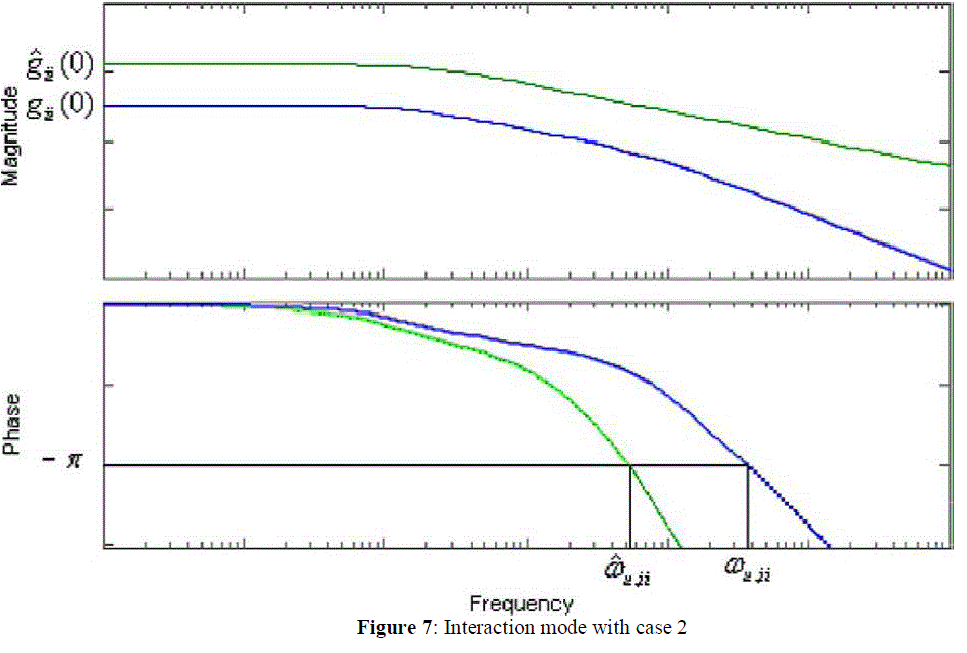
Notice that grij(s) is usually low order transfer functions, their contribution to the phase change at low frequency range are small and can be equivalently represented by the additional time delay term. In many decentralized control system designs, such as gain and phase margin method, an individual loop is tuned around the critical frequency region of each control loop. Accurate estimation of overall variation is required around the critical frequency, not who contribute to the change.

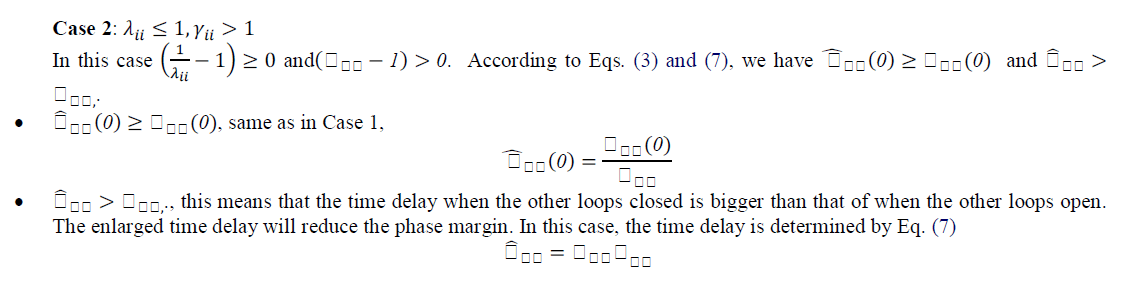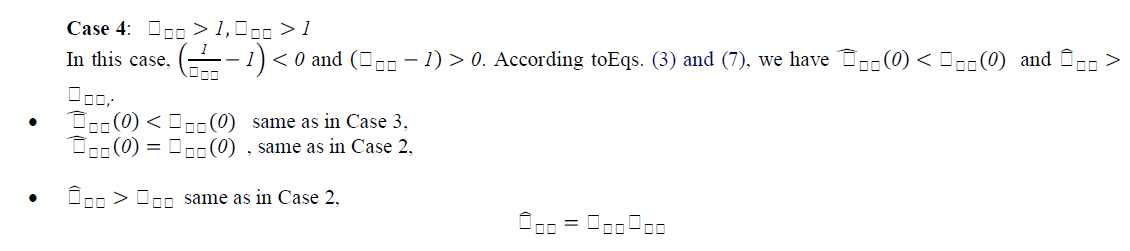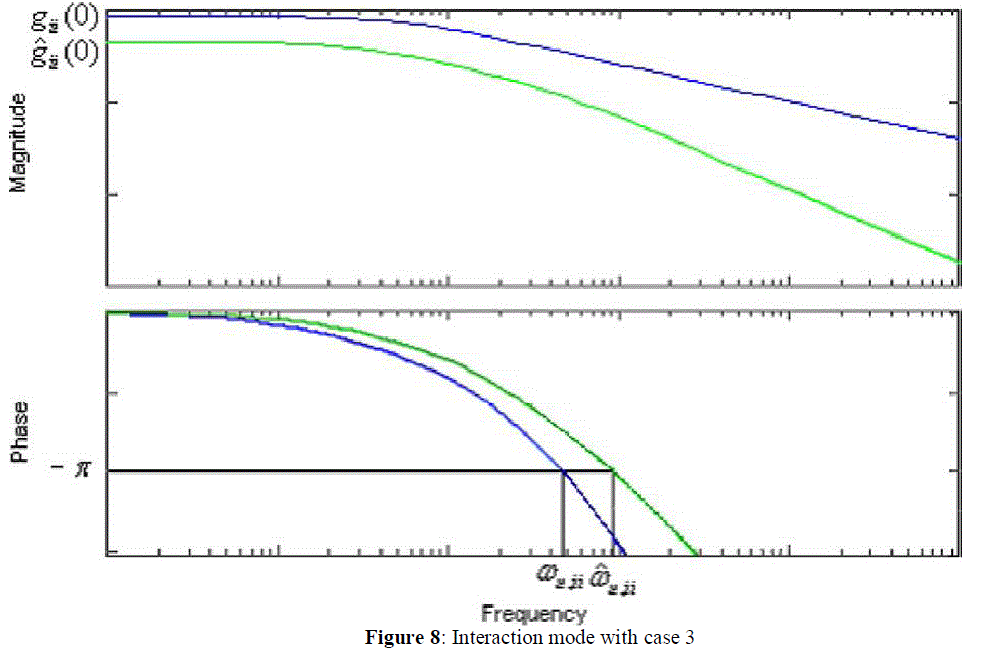
A unique problem for decentralized control of MIMO processes is the zero crossing: stable or unstable zeros might be introduced into a particular control loop when other loops are closed. If an unstable zero is introduced, it will result phase shift to the left in the frequency domain. In order to guarantee the entire system stability, the controllers are normally conservatively designed by conventional detuning approaches. By introducing the relative critical frequency,������, to indicate phase changes after the other loops closed, the effects of unstable zeros can be accurately estimated in each control loop. Consequently, the resultant control systems will be much less conservative.

Mathematically, the equivalent transfer function should incorporate the controllers of all other loops.

To solve such a complex problem, recursive solution is required by first assigning initial controllers, then finding the equivalent loop transfer functions and designing controllers again. This process is continuous until a stable solution is obtained. To simplify the problem, both detuning and independent methods proposed so far assume that all other closed loops are under perfect control when designing the controller for a particular loop and consider only the gain change. In the proposed method, the changes are considered for both gain and frequency. Especially, Eq. (3) focuses on the gain impact while Eq. (7) contributes to time delay portion, i.e., frequency impact. As will be shown later, it is far more accurate than those existing methods

DECENTRALISED CONTROL SYSTEM DESIGN

Without loss of generality, we assume that each main loop, i.e., diagonal element in the transfer function matrix is represented by a second order plus dead time (SOPDT) model, which can be used to describe most of the industrial processes:

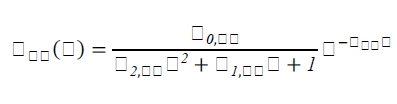Similarly, ETF is represented as,

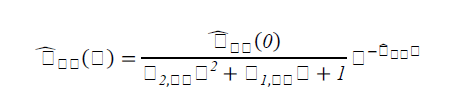The decentralized controllers can then be independently designed by single loop approaches based on the corresponding ETFs. Here we employ the gain and phase margins approach. This is primary because the frequency response method provides good performance in the face of uncertainty in both plant model and disturbances.

The PID controller of each loop is supposed of the following standard form:

CONCLUSION

Effective transfer function approach is a novel method for decentralized control system design of multivariable interactive processes. An extension of the effective transfer function approach by taking into consideration all the interactions was proposed and implemented successfully with improved responses. The simplicity and effectiveness of the method is based on the incorporation of the interaction frequency directly in the controller design. This approach ensures that all the necessary information of the gain and interaction frequency changes are provided. The decentralized controllers are obtained by simply using the single loop design approaches. Simulation results for the four 2x2 processes and a 3x3 process show that the proposed method provides a better overall performance compared to the other design approaches even after taking into account the interactions. The advantage of this method is more significant when applied to higher dimensional processes with complicated interaction modes. Since this is an extension of the ETF approach, it can also be easily integrated into an auto-tuning control structure. This method can also be successfully tested for the other MIMO processes. Also employment of BLT tuning after obtaining the effective transfer function can also be performed for better results.

References

W.L.Luyben, M.L.Luyben, Essentials of process control, McGraw-Hill Chemical Engineering Series, 1997. Qiang Xiong, Wen-Jian Cai, Effective transfer function method for decentralized control system of MIMO processes,JPC 16(2006). Deshpande, P.B. (1989), Multivariable Process Control, ISA, North Carolina. W.L.Luyben, Simple Method for Tuning SISO Controllers in Multivariable Systems, I&EC Process Design and Development ,Vol. 25, No.3,1986 George Stephanopoulos, Chemical Process Control – An Introduction to theory and practice, Prentice Hall Of ndia,2008