ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Girish Kumar1 and Rameshwar singh2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper presents an algorithm for solving optimal power flow problem through the application of Differential Evolution (DE). Reduction in fuel costs done of power generation by proper load dispatch schedule. So the overall costing of operation of power system can be reduced. The differential evolution algorithm is an evolutionary algorithm that uses a rather greedy and less stochastic method than do classical evolutionary algorithms such as particle swarm optimization (PSO) .Differential Evolution also incorporates an efficient way of self-adapting mutation using small population. The effectiveness of algorithm has been tested for a practical economic dispatch problem on a test system having three generating units. Thermal power generating firms needs to minimize fuel cost, for better profit at the same time it should satisfy system load demand, real, reactive power limit, voltage limit, power transmission limit and other limitations. For generation cost minimization Economic Load Dispatch (ELD) was developed. When cost is the single objective, the power generation may pollute the environment. Thermal electric power could not be generated without pollution but this pollution can be reduced for the sake of good and healthy atmospheric condition. To reduce emission the firm has to spent money, which is burden and reduces the power generating firms profit. These two opposite objectives should be compromised to find optimal operating condition of thermal power plants which may yield minimum fuel cost. Differential Evolution (DE) algorithm is used to solve this complex problem.
Keywords |
| Optimization, Economic load dispatch, Differential Evolution, PSO. |
INTRODUCTION |
| Power utilities try to achieve high operating efficiency to produce cheap electricity. Competition exists in the electricity supply industry in generation and in the marketing of electricity. The operating cost of a power pool can be reduced if the areas with more economic units generate larger power than their load, and export the surplus power to other areas with more expensive units. Benefits thus gained will depend on several factors like the characteristics of a pool, the policies adopted by utilities, types of interconnections, tie-line limits and load distribution in different areas. Therefore, transmission capacity constraints in production cost analysis are important issues in the operation and planning of electric power systems [1]. The Differential Evolution is a parallel direct search method proposed by Storm and Price in 1995.[2][3] DE is a population based stochastic function maximize relating to evolutionary computation, whose simple yet powerful and straightforward features make it very attractive for numerical optimization. DE uses a rather greedy and less stochastic approach to problem solving than do evolutionary algorithms (EA). DE combines simple arithmetical operators with the classical operators of recombination, mutation, and selection to evolve from a randomly generated starting population to a final solution. DE differs from conventional genetic algorithms in its use of perturbing vectors, which are the difference between two randomly chosen parameters vectors. This method is a heuristic, population-based optimization method that uses a population of points to search for global minimum of a function over continuous search space. DE generates new vectors of parameters by adding the weighted difference between two vectors to a third one. If the result provides a smaller objective function than a predetermined individual, new result will replace the one with which it is compared. DE has been used to solve different optimization problems including power system planning, however, the main difficulty with DE techniques, appears to be ensuring the search diversity of population when the algorithm is approaching the region of local and global optimum. The improvement is mainly achieved through several mutation methods by combining the fitness sharing scheme into the solution process. The findings are supported by detailed simulations based on mathematical function optimization before solving a power system planning problem. The objective of the economic dispatch problem (EDP) of electric power generation, whose characteristics are complex and highly nonlinear, is to schedule the committed generating unit outputs so as to meet the required load demand at minimum operating cost while satisfying all units and system equality and inequality constraints. Chaos describes the complex behaviour of a nonlinear deterministic system. The application of chaotic sequences instead of random sequences in DE is a powerful strategy to diversify the DE population and improve the DE’s performance in preventing premature convergence to local minima. |
ECONOMIC LOAD DISPATCH (ELD) |
| The objective of an ELD problem is to find the optimal combination of power generations that minimizes the total generation cost while satisfying equality and inequality constraints [5,6]. The fuel cost curve for any unit is assumed to be approximated by segments of quadratic functions of the active power output of the generator. For a given power system network, the problem may be described as optimization (minimization) of total fuel cost as defined by (1) under a set of operating constraints. |
| (a) ELD Problem without Valve-Point Effects |
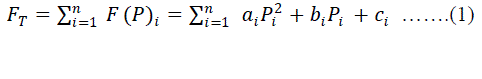 |
| Where is FT total fuel cost of generation in the system ($/hr), ai, bi, and ci are the cost coefficient of the i th generator, Pi is the power generated by the i th unit and n is the number of generators. |
| The objective of ELD is to minimize the overall cost of generation. Power balance constraint The total generation cost is minimized subjected to the following constraints Power balance constraint power balance constraint |
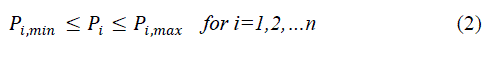 |
| Generation capacity constraint |
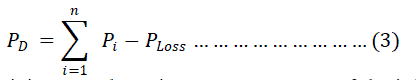 |
| where Pi, min and Pi, max are the minimum and maximum power output of the i th unit, respectively. PD is the total load demand and PLoss is total transmission losses. The transmission losses PLoss can be calculated by using B matrix technique and is defined by (4) as, |
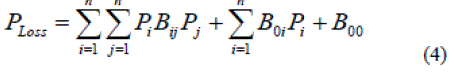 |
| where Bij is coefficient of transmission losses. |
| (b) ELD Problem Considering Valve-Point Effects |
| The generating units with multi-valve steam turbines exhibit a greater variation in the fuel-cost functions, The valve opening process of multi-valve steam turbines produces a ripple-like effect in the heat rate curve of the generators. These âÃâ¬Ãâ¢valve-point effects are illustrated in Fig. 1. The significance of this effect is that the actual cost curve function of a large steam plant is not continuous but more important it is non-linear. |
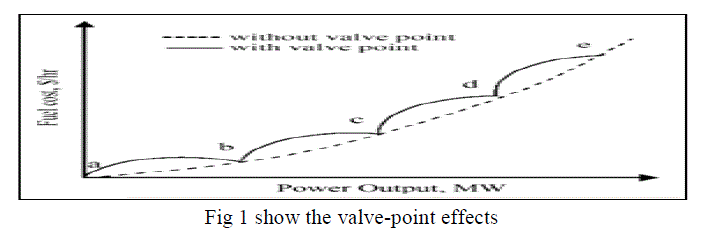 |
| The valve-point effects are taken into consideration in the ELD problem by superimposing the basic quadratic fuel-cost characteristics with the rectified sinusoid component as follows: |
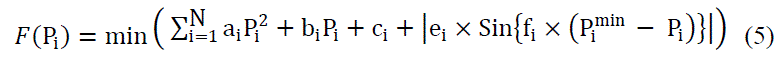 |
| where Fp(i) is total fuel cost of generation in ($/hr) including valve point loading, ei, fi are fuel cost coefficients of the i th generating unit reflecting valve-point effects. Minimizing the total fuel cost of the thermal power plants while satisfying the demand power and power system constraints is aimed at to overcome the ED problem [7]. |
DIFFERENTIAL EVOLUTION ALGORITHM |
| (a) Evaluation |
| Differential Evolution is one of the most recent population based stochastic evolutionary optimization techniques. Storn and Price first proposed DE in 1995 [2, 3] as a heuristic method for minimizing non-linear and non-differentiable continuous space functions. DE algorithm is a simple population based evolutionary computational algorithm for global optimization .It is one of the accurate and fast meta-heuristic optimization algorithms that was introduced in 1995s by Price and Storn.This evolutionary algorithm begins the search process by initial random population. DE includes three main operators, namely, mutation, crossover, and selection. Also, it has three control parameter, namely, population size (np), scaling coefficient (F), and crossover probability (CR) [8, 9, 10]. Differential Evolution includes Evolution Strategies (ES) and conventional Genetic Algorithms (GA). Differential Evolution is a population based search algorithm, which is an improved version of Genetic Algorithm. One extremely powerful algorithm from Evolutionary Computation due to convergence characteristics and few control parameters is differential evolution. Like other evolutionary algorithms, the first generation is initialized randomly and further generations evolve through the application of certain evolutionary operator until a stopping criterion is reached. The optimization process in DE is carried with four basic operations namely, Initialization, Mutation, Crossover and Selection. |
| (b) Initialization |
| The algorithm starts by creating a population vector of size P N given by equation (5) composed of individuals that evolve over G generation. From the equation (6) each individual (G) i X, is a vector that contains as many elements as the problem decision variable. The population size P N is an algorithm control parameter selected by the user. Each individual or candidate solution is a vector that contains as many parameters as the problem decision variables D. In Differential Evolution the population size P N, remains constant throughout the optimization process. |
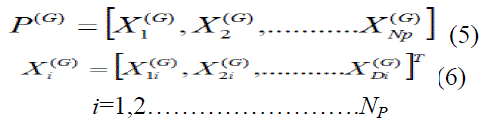 |
| The first step in the DE optimization process is to create an initial population of candidate solutions by assigning random values to each decision parameter of each individual of the population. The initial population is chosen randomly in order to cover the entire searching region uniformly. A uniform probability distribution for all random variables is assumed as in the following equation |
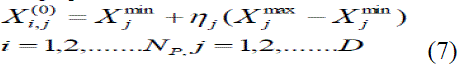 |
| Where Xjmin and Xjmax are respectively, the lower and upper bound of the decision parameter and nj is a uniformly distributed random number within [0, 1] generated anew for each value of j. |
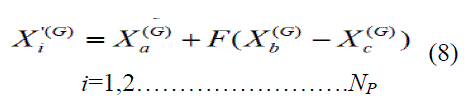 |
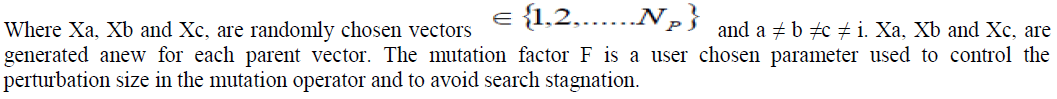 |
| Crossover Operation |
| The crossover operation generates trial vectors by mixing the parameter of the mutant vectors with the target vectors. For each parameter, a random value based on binomial distribution is generated in the range [0, 1] and compared against a user defined constant referred as crossover constant. If the random number is less than the crossover constant the parameter will come from the mutant vector, otherwise the parameter comes from parent vector as in equation (9). The crossover operation maintains diversity in the population, preventing local minima convergence. The crossover constant (CR) must be in the range of [0, 1]. A crossover constant of one means the trial vector will be composed entirely of mutant vector parameters. A crossover constant near zero results in more probability of having parameters from target vector in trial vector. A randomly chosen parameter from mutant vector is always selected to ensure that the trial vector gets at least one parameter from mutant vector even if the crossover constant is zero. Trial vectors are generated according to |
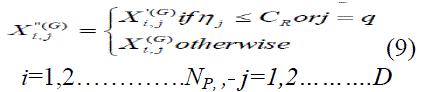 |
 |
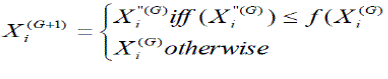 i=1,2………….NP, (10) i=1,2………….NP, (10) |
| their fitness while exploring the solution space for optimal values. The iterative process of mutation, crossover and selection on the population will continue until a user-specified stopping criterion, normally, the maximum number of generations allowed, is met. The other type of stopping criterion, i.e. convergence to the global optimum result. |
RESULT AND DISCUSSION |
| Proposed DE Algorithm has been applied to ED problems in test cases for verifying its feasibility. These are a three unit’s system show in the table 1 and power Demand 850 MW [4]. The software has been written in MATLAB-7 language. |
 |
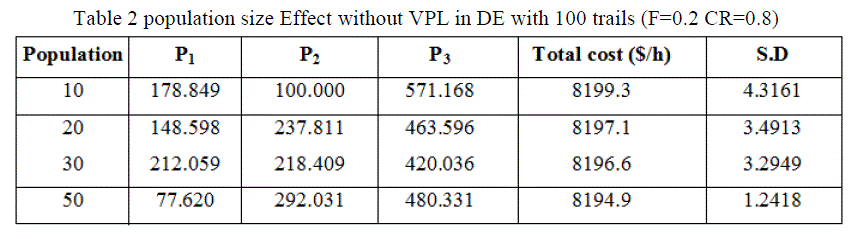
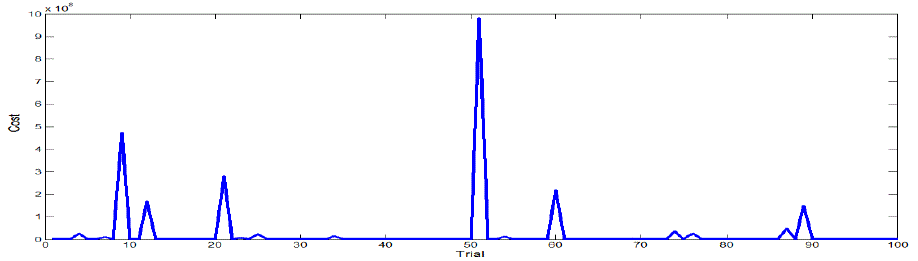
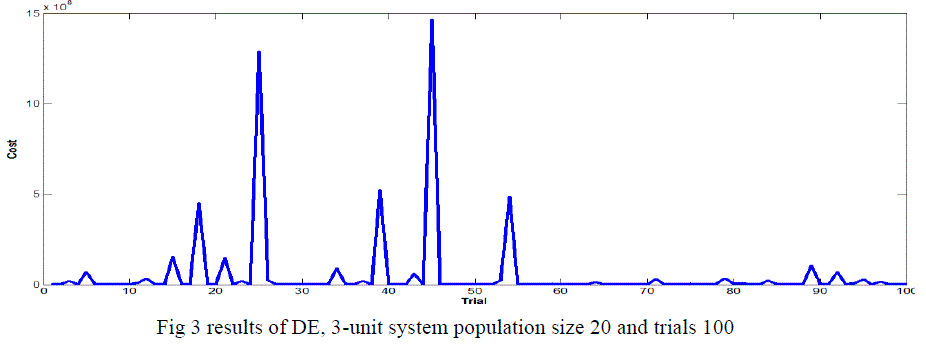
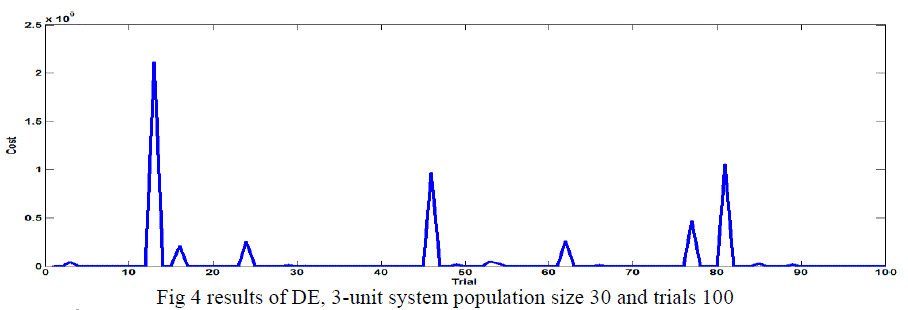
Case 1 Population Size Effect in 3-Generating Units without VPL |
| In this paper, tests were carried out for different population sizes, the various ELD problems, larger the dimension, larger is the population size required to achieve good results, so increase the population sizes ,Achieved the minimum global results. The DE algorithm converges to the global best solution for the 3-unit system for a population size of 10.20,30 and 50 shows in the table 3 and fig 2, fig 3, fig 4 and figures 5 in this case use C.R 0.8 or F 0.2 with 100 trails. DE achieved quite effective result. |
 |
 |
 |
 |
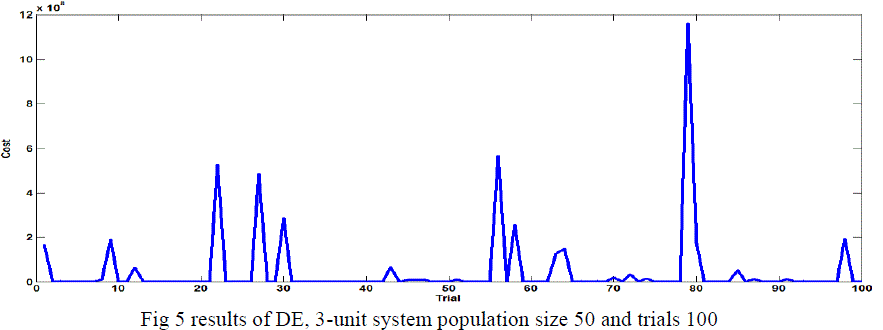 |
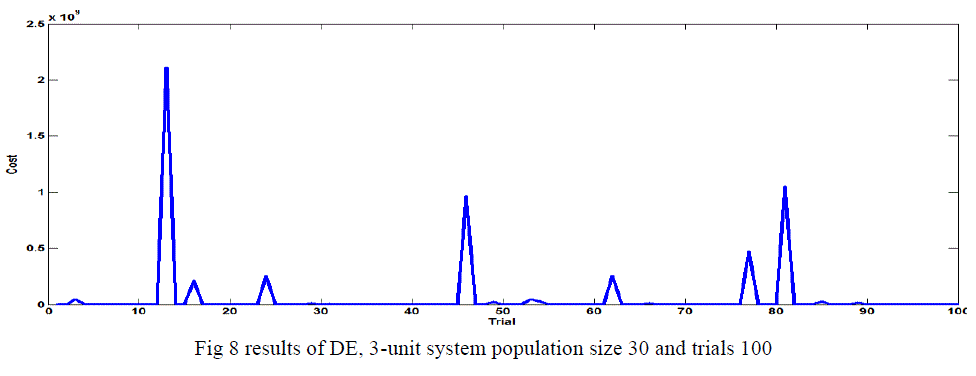
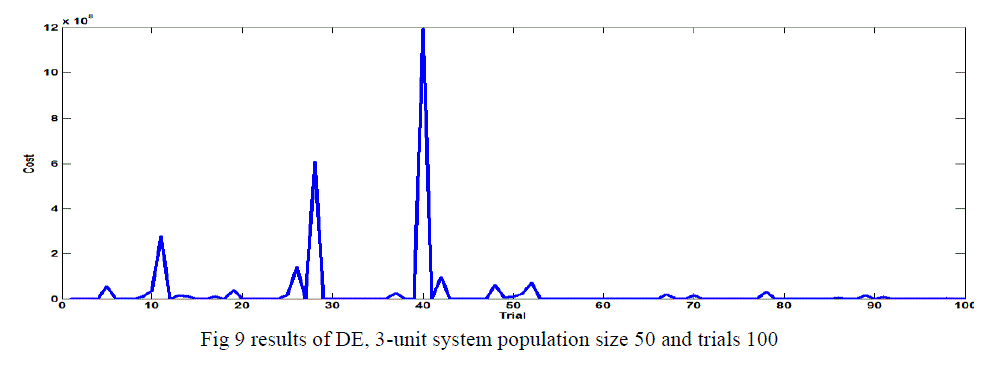
Case ii Population Size Effect in 3-Generating Units with VPL |
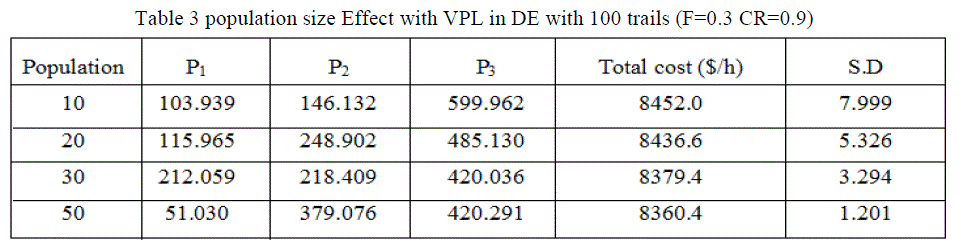
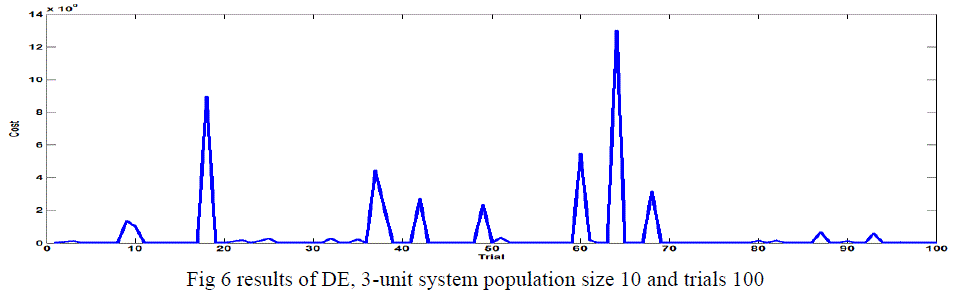
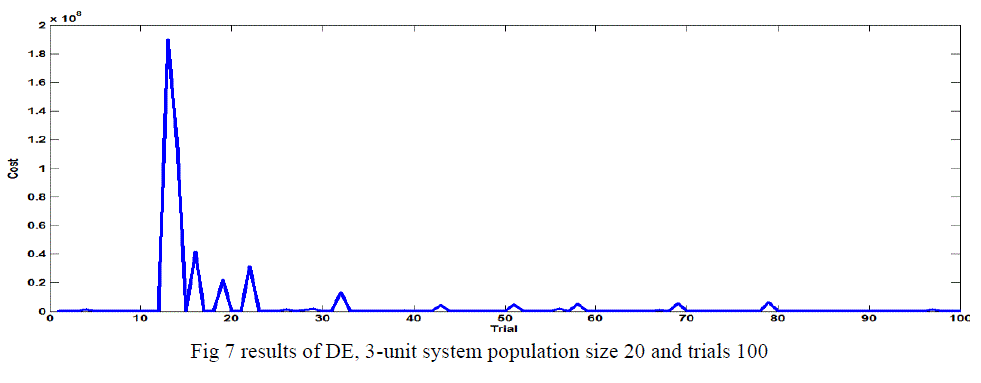
| The DE algorithm converges to the global best solution for the 3-unit system for a population size of 10.20,30 and 50 show in the table 4 and fig 6, fig 7, fig 8 and figures 9 in this case use C.R 0.9 or F 0.3 with 100 trails. |
 |
 |
 |
 |
 |
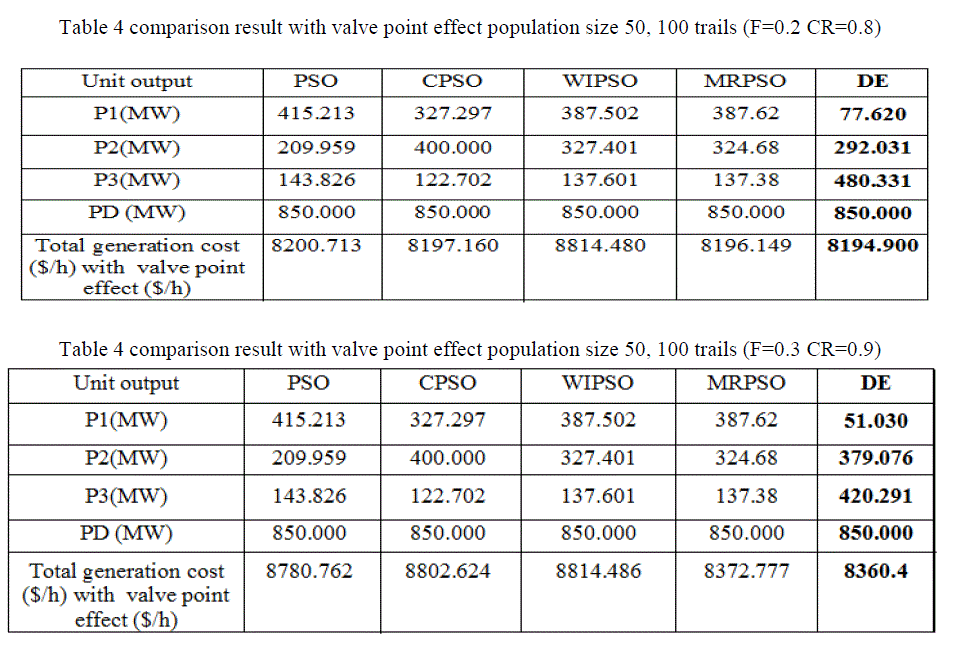
| Case iii Comparative analysis |
| The Comparative analysis DE with achieved quite effective result. A parameter tuning was done to find optimal values of C.R 0.8 or F 0.2 with Population sizes 50 out of 100 trails in without valve Point Loading, Comparative result show in the table 4 and C.R. 0.9 or F 0.3 with Population sizes 50 out of 100 trials for with valve Point Effects practical Comparative result show in the table 5, Results obtained DE algorithm have been compared then vest result with PSO,CPSO,WIPSO and MRPSO [4], DE achieved quite effective result and global best solutions. |
 |
CONCLUSION |
| The differential evolution algorithm has been successfully implemented to solve ED problems with the generator constraints as linear equality and inequality constraints the algorithm is implemented for three units system. From the result, it is clear that the proposed algorithm has the ability to find the better quality solution, computational efficiency, less CPU time and minimum S.D. per iteration when compared to other methods such as PSO and PSO variant. |
References |
|